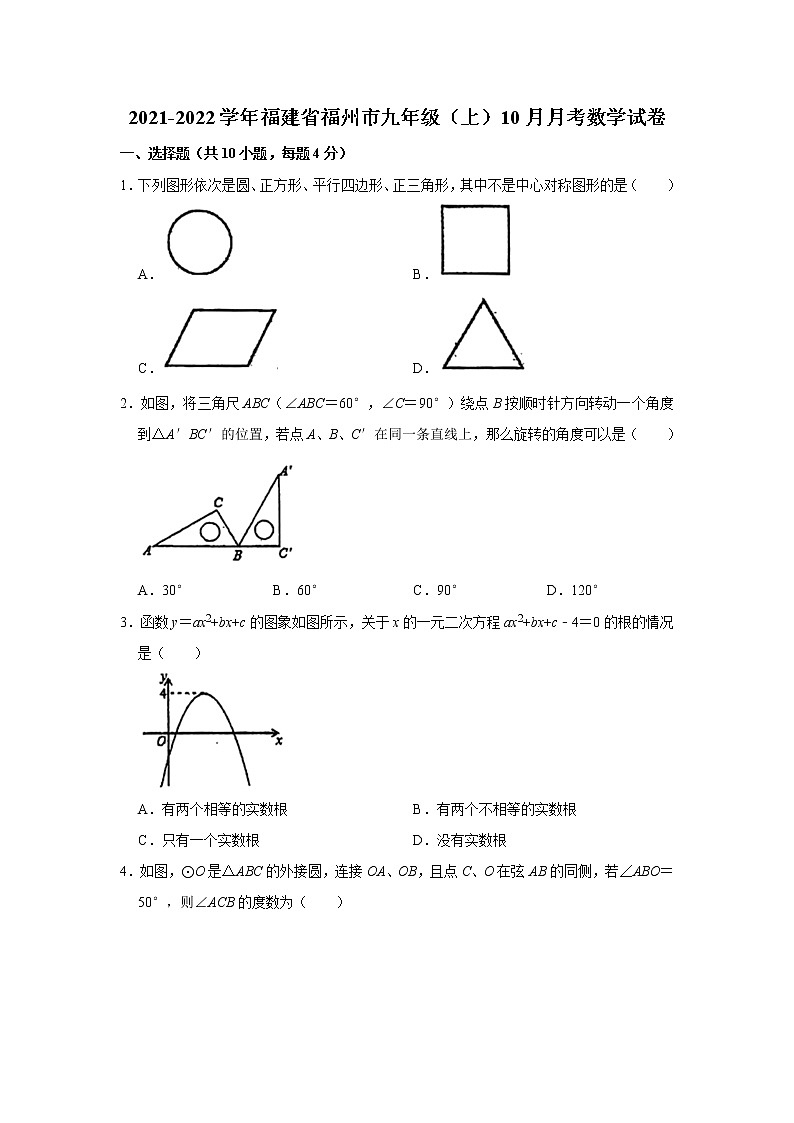
2021-2022学年福建省福州市九年级（上）10月月考数学试卷(Word版无答案)

这是一份2021-2022学年福建省福州市九年级（上）10月月考数学试卷(Word版无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．下列图形依次是圆、正方形、平行四边形、正三角形，其中不是中心对称图形的是（ ）
A．B．
C．D．
2．如图，将三角尺ABC（∠ABC＝60°，∠C＝90°）绕点B按顺时针方向转动一个角度到△A′BC′的位置，若点A、B、C′在同一条直线上，那么旋转的角度可以是（ ）
A．30°B．60°C．90°D．120°
3．函数y＝ax2+bx+c的图象如图所示，关于x的一元二次方程ax2+bx+c﹣4＝0的根的情况是（ ）
A．有两个相等的实数根B．有两个不相等的实数根
C．只有一个实数根D．没有实数根
4．如图，⊙O是△ABC的外接圆，连接OA、OB，且点C、O在弦AB的同侧，若∠ABO＝50°，则∠ACB的度数为（ ）
A．50°B．45°C．30°D．40°
5．用配方法解方程x2﹣4x+1＝0，则方程可变形为（ ）
A．（x﹣2）2＝5B．（x﹣2）2＝3C．（x﹣1）2＝3D．（x﹣4）2＝1
6．已知二次函数y＝﹣x2+（m﹣1）x+1，当x＞1时，y随x的增大而减小，而m的取值范围是（ ）
A．m＝﹣1B．m＝3C．m≥﹣1D．m≤3
7．筒车是我国古代发明的一种水利灌溉工具，如图1，筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2．已知圆心O在水面上方，且⊙O被水面截得的弦AB长为6米，⊙O半径长为4米．若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是（ ）
A．1米B．(4−7)米C．2米D．(4+7)米
8．如图，将等边三角形OAB放在平面直角坐标系中，A点坐标（1，0），将绕点力顺时针旋转60°，则旋转后点B的对应点B′的坐标为（ ）
A．(12，32)B．(1，12)C．(32，32)D．(32，12)
9．如图是一个长20cm，宽15cm的矩形图案，其中有两条宽度相等，互相垂直的彩条，彩条所占面积是图案面积的14，设彩条的宽度为xcm，则下列方程正确的是（ ）
A．20x+15x−x2=14×15×20
B．(20−x)(15−x)=14×15×20
C．20x+15x=14×15×20
D．20x+15x+x2=14×15×20
10．二次函数y＝ax2+b（a＜0）的图象过A（﹣2，y1），B（6，y1），C（0，y2），D（3，y3），E（5，y4）五个点，下列说法一定正确的是（ ）
A．若y1y2＞0，则y3y4＞0B．若y1y4＞0，则y2y3＞0
C．若y2y4＜0，则y1y3＜0D．若y3y4＜0，则y1y2＜0
二、填空题（共6小题，每题4分）
11．点A（a，3）与点B（﹣4，b）关于原点对称，则a+b＝ ．
12．已知x＝1是关于x的方程x2+ax﹣2＝0的一个根，则此方程的另一根为 ．
13．已知A，B，C三点在⊙O上，若∠ACB＝130°，则∠AOB＝ ．
14．函数y＝x2+6x﹣9的最小值为 ．
15．抛物线y＝ax2与直线y＝bx+c交于两点（﹣2，4）、（1，1），则方程ax2＝bx+c的解是 ．
16．已知：如图，在正方形ABCD内取一点P，连接PA、PB、PD，将△PDA绕点A顺时针旋转90°得△EBA，连EP．若PA＝2，PB＝25，PD＝23．下列结论：①EB⊥EP；②点B到直线AE的距离为6；③S△APD+S△APB＝1+6；④S正方形ABCD＝16+46．其中正确结论的序号是 ．
三、解答题（共9小题，共86分）
17．解方程：x2﹣4x﹣1＝0．
18．如图，△ABC的顶点及点O都在正方形网格格点上．
（1）画出△ABC关于点O中心对称的图形△A1B1C1；
（2）画出△ABC绕点O顺时针旋转90°的图形△A2B2C2．
19．已知关于x的一元二次方程2x2+（2k+1）x+k＝0．
（1）求证：方程总有两个实数根；
（2）若该方程有一个根是正数，求k的取值范围．
20．如图，AB是⊙O的直径，C是BD的中点，CE⊥AB于点E，BD交CE于点F．
（1）求证：CF＝BF；
（2）若CD＝6，AC＝8，求⊙O的半径及CE的长．
21．如图，抛物线y＝x2+2x﹣3与x轴交于A、B两点（点A在点B左侧），交y轴于点C，抛物线的顶点为点D．
（1）求AB的长度和顶点D的坐标；
（2）请你写出一种平移方法，使抛物线经过平移后与坐标轴只有两个交点．（不需证明）
22．在△ABC中，AC＝BC，∠ACB＝90°，将△ABC绕点A顺时针旋转一定角度α，得到△ADE，点B，C对应点分别是D，E．
（1）如图1，当点E恰好在AB上时，求∠BDE的度数；
（2）如图2，点F是边AB的中点，当α＝90°时，请证明E，F，C三点共线．
23．如图，有长为21m的篱笆，一面利用墙（墙的最大可用长度为10m）围成中间隔有一道篱笆的长方形养鸡场，设养鸡场的宽AB为xm，面积为ym2．
（1）y与x的函数关系为 ，其中x的取值范围为 ，函数图象的对称轴为 ；
（2）当养鸡场的面积为18m2时，求养鸡场的宽；
（3）求养鸡场面积的最大值．
24．（一）问题情境：
如图1，已知点E，F分别在正方形ABCD的边AB，BC上，且BE＝BF，点M为AF的中点，连接CE，BM．
（1）线段CE与BM之间的数量关系是 ，位置关系是 ．
（二）猜想证明：
（2）如图2，将线段BE和BF绕点B逆时针旋转，旋转角均为α（0°＜α＜90°）．点M为线段AF的中点，连接BM，请你判断（1）中的两个结论是否仍然成立．若成立，请证明；若不成立，请说明理由．
（三）探索发现：
（3）将图1中的线段BE和BF绕点B逆时针旋转，旋转角为α＝90°，点M为线段AF的中点，得到如图3所示的图形，请你判断线段CE与BM之间的数量关系是否发生变化，请说明理由．
25．已知抛物线y＝x2+bx+c．
（1）当抛物线对称轴为y轴，且经过点（﹣2，1）时，求抛物线解析式；
（2）已知直线y＝x﹣2与该抛物线交于A，B两点．
①当线段AB被x轴平分时，求b的值；
②若抛物线y＝x2+bx+c与x轴相交，且当x＜﹣1时，y随x的增大而减小，△AOB的面积为2，求c的取值范围．