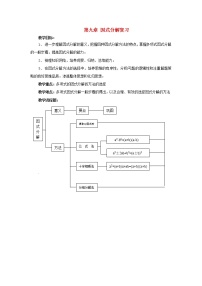
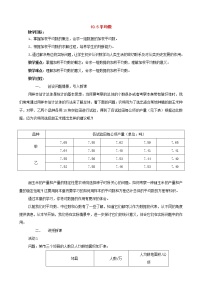
数学七年级下册6.3 整式的乘法教学设计

这是一份数学七年级下册6.3 整式的乘法教学设计，

§7.3.3多项式乘以多项式一、教学目标：1. 使学生会进行多项式乘以多项式的运算。理解多项式乘以多项式的几何意义。提高运算能力，并进行简单的应用。2. 通过运算的转化、整式乘法渗透数形结合、换元等数学方法和“转化”的数学思想。3. 培养学生观察、归纳、猜想、论证的能力，使学生了解和体会“特殊---一般的---特殊”的认识规律，体验和学习研究问题的方法。培养学生严谨认真的学习态度，二、重点：多项式乘多项式三、难点： 1）漏乘与重复乘。 2）运算符号易出错四、教学方法： 组织小组讨论法、发现教学法五、教学过程：六、复习引入：（投影片）1.单项式的乘法法则是什么？2.怎样计算单项式与多项式的乘法？3. (a+b)X= ?七、探索新知、想 一 想：（投影片）当X=m+n时, (a+b)X=?由上一题知 (a+b)X=aX+bX于是，当X=m+n时(a+b)X=(a+b)(m+n)=a(m+n)+b(m+n)=am+an+bm+bn即 (a+b)(m+n)=am+an+bm+bn “整体换元”思想，“转化”思想：先把(m+n)看作一个单项式（整体），就可以把多项式与多项式相乘转化为单项式与多项式相乘。(m+n)(a+b+c)=(m+n)a+ (m+n)b+ (m+n)c=ma+na+mb+nb+mc+nc说明：在放投影片时，进行分组讨论，得出结论。多项式的乘法法则多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.例1 计算:(1) (x+2y)(5a+3b) ;解：(x+2y)(5a+3b) ==5ax+3bx+10ay+6by(2) (2x–3)(x+4) ;解：(2x–3)(x+4)==(3) (3x+y)(x–2y) ；解：(3x+y)(x–2y)=课堂练习：练习一、计算：(1) (2n+6)(n–3);(2) (2x+3)(3x–1);(3) (2a+3)(2a–3);(4) (2x+5)(2x+5).注意：多项式乘以多项式，展开后项数很有规律，在合并同类项之前，展开式的项数恰好等于两个多项式的项数的积。练习二、计算：(1) (x–1)(x2+x+1) ;(2) (2a+b)2;(3) (3a–2)(a–1)–(a+1)(a+2) ;(4) (x+y)(2x–y)(3x+2y).八、小结：今天我们学了什么？1。今天学习了多项式 的乘法。法则是什么？2。多乘多应注意的问题是什么？3。检查是否漏乘的方法是什么？九、作业：p84.10.11十、板书设计课后记：