数学北京课改版第十二章 三角形12.4 全等三角形课堂教学ppt课件

这是一份数学北京课改版第十二章 三角形12.4 全等三角形课堂教学ppt课件，

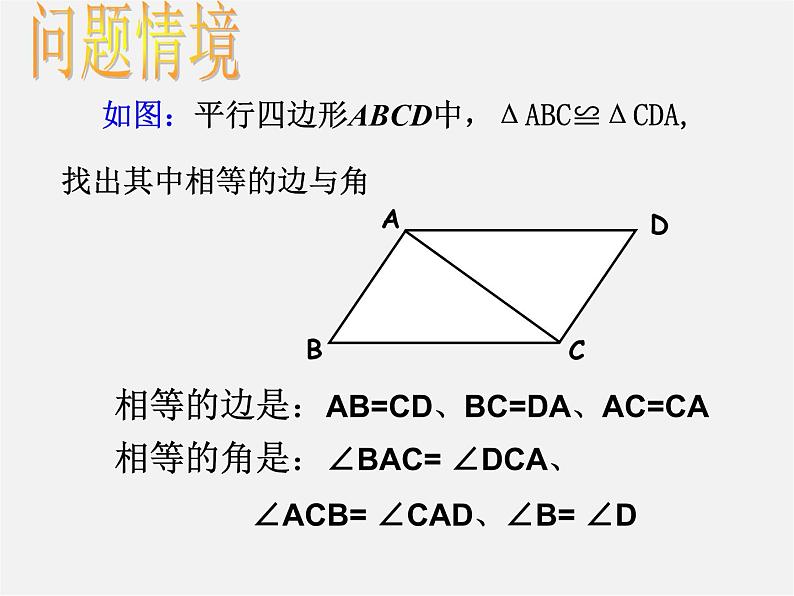
全等三角形13.4 全等三角形 如图：平行四边形ABCD中，ΔABC≌ΔCDA,找出其中相等的边与角相等的边是：AB=CD、BC=DA、AC=CA相等的角是：∠BAC= ∠DCA、 ∠ACB= ∠CAD、∠B= ∠D问题情境问题情境 你是如何识别两个三角形全等的? 我们能不能找到一些较为简便的方法，用来识别三角形的全等呢？有没有类似于相似三角形的识别方法呢？ 全等三角形的识别做一做1、只给一个条件（一条边或一个角）画三角形时，大家画出的三角形一定全等吗？(1) 三角形的一条边为3cm(2)三角形的一个内角分别为60°不一定全等做一做2、给出两个条件画三角形时，有几种可能的情况？每种情况下作出的三角形一定全等吗？分别按照下面的条件做一做： (1) 三角形的一个内角为60°，一条边为3cm(2)三角形的两个内角分别为30°和70°(3)三角形的两条边分别为3cm，5cm不一定全等议一议 如果给出三个条件画三角形，你能说出有哪几种可能的情况？三个角三条边两边一角两角一边 已知一个三角形的三个内角分别为40°，60°和80 ° ，你能画出这个三角形吗？把你画的三角形与同伴画的进行比较，它们一定全等吗？ 三个内角对应相等的两个三角形不一定全等做一做如果两个三角形的三条边分别对应相等，那么这两个三角形会全等吗？做一做给你三条线段a、b、c，以这三条线段为边画一个三角形。步骤：1、画一线段AB使它的长度等于 c（4.8cm）2、以点A为圆心，以线段b （3cm）的长为半径画圆弧； 以点B为圆心，以线段a （4cm）的长为半径画圆弧； 两弧交于点C3、连结AC、BC⊿ABC即为所求做一做发 现把你画的三角形与其他同学的图形相比较，他们全等吗？叠合在一起，是否完全重合？换三条线段，再试试看，是否有同样的结论。发现：给定三条线段，如果它们能组成三角形，那么所画的三角形都是全等的。识别三角形全等的一种简便的方法：如果两个三角形的三条边分别对应相等，那么这两个三角形全等。（sss）概括 三边对应相等的两个三角形全等简写为“边边边”或“SSS”概括___________________________________如图：∵∴ΔABC≌ΔDEF (sss)在⊿ABC和⊿ DEF中AB=DE，AC=DF，BC=EF∵OD=OE,CD=CE,∴∆OCD≌∆OCE∴∠DOC=∠EOC∴OC为∠AOB的平分线解： 例1：有一种作已知角的平分线的方法，如图，在∠AOB的两边上分别取点D、E，使OD=OE，再分别以D、E为圆心，大于 DE长为半径作弧,两弧相交于点C，作射线OC，则OC就是∠AOB的平分线。试说明这种作法的正确性。连结EC、DCOC=OC例题解析在⊿OCD和⊿ OCE中1、根据条件判定下面的三角形是否全等？ （1）（2）（3）（4）相信自己1、两个等边三角形全等（ ）2、两条直角边对应相等的两个直角三角形全等（ ）3、两个等腰直角三角形全等（ ）4、都有两边长分别为3厘米和5厘米的两个等腰三角形全等（ ）5、都有两边长分别为3厘米和8厘米的两个等腰三角形全等（ ）√××××2、判断题（对打“√”，错打“× ”：相信自己 3、如图：已知AB=CD，AD=BC，要求∠DCA=∠BAC，需先求⊿___≌⊿___，所用全等识别法是_______。所需要的条件是：_______, ______, _____。 相信自己 3、如图，四边形ABCD是平行四边形，△ABC和△CDA是否全等？若四边形是菱形、矩形、梯形，是否还有相同的结论？相信自己4、已知：如图，点A、B、C、D在同一条直线上，AC=BD，AM=CN，BM=DN试说明：AM∥CN，BM∥DN相信自己5、三月三，放风筝，如图所示是小芳制作的风筝。她根据DE=DF，EH=FH，不用度量，就知道∠DEH=∠DFH，请你用所学知识给予证明。 （2004、福建福州）DEHF超越自我感悟与反思1、由实践知，对于两个三角形的三条对应边、三个对应角中，只有满足其中一个条件或两个条件相等，两个三角形不一定全等。 2、可用（SSS）来识别两个三角形全等；三个角对应相等的两个三角不一定会全等。 3、两个全等三角形是否相似？再见谢谢大家