沪科版八年级上册12.2 一次函数示范课课件ppt

这是一份沪科版八年级上册12.2 一次函数示范课课件ppt，共19页。PPT课件主要包含了2一次函数，例题讲解等内容，欢迎下载使用。

问题一：甲乙两地相距250千米，一辆汽车以50千米/时的速度从甲地开往乙地.汽车距乙地的路程S与速度t之间的函数关系式为： S=250-50t问题二：一热气球从海拔550米的山上以5米/秒的速度向上升起.热气球的海拔高度h与时间t的函数关系式为： h=550+5t
这两个函数解析式有什么共同特点呢？
一般地，如果变量y与变量x有关系式： y=kx+b(k,b是常数，且k≠0) 那么，y叫做x的一次函数
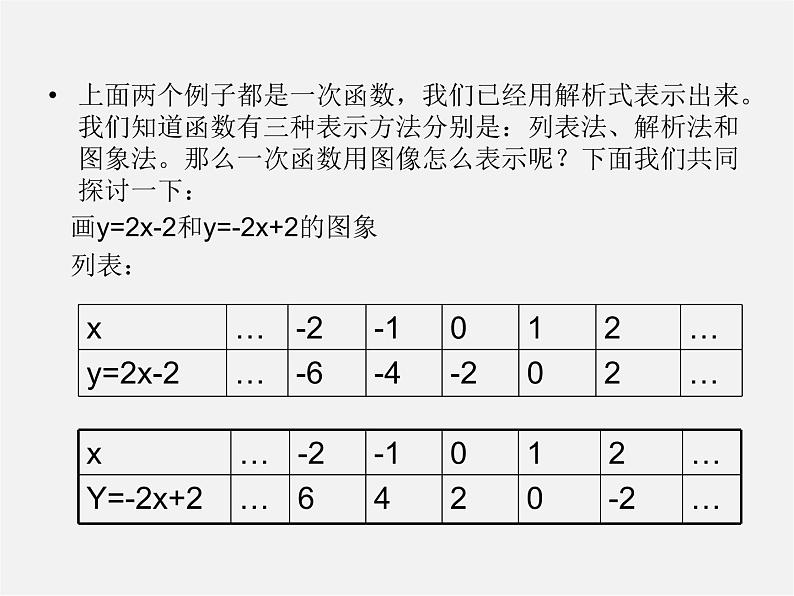
上面两个例子都是一次函数，我们已经用解析式表示出来。我们知道函数有三种表示方法分别是：列表法、解析法和图象法。那么一次函数用图像怎么表示呢？下面我们共同探讨一下： 画y=2x-2和y=-2x+2的图象 列表：
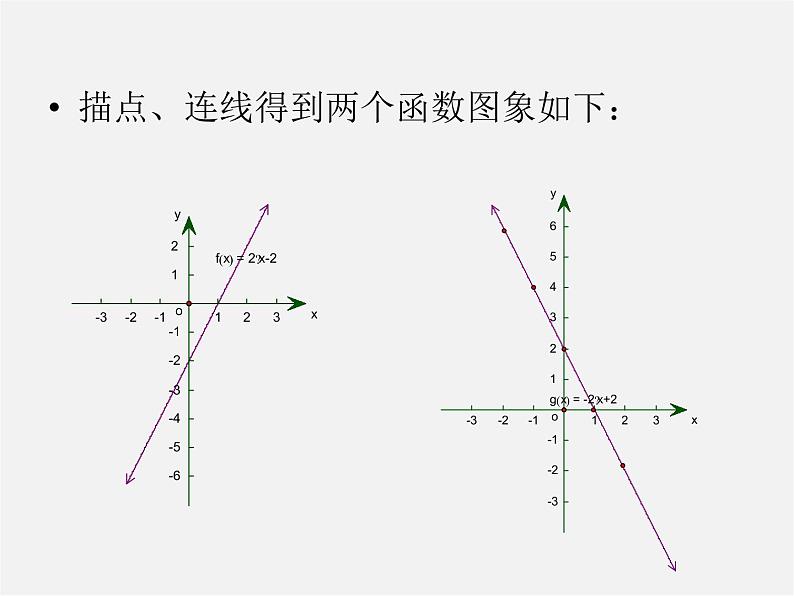
描点、连线得到两个函数图象如下：
一次函数y=kx+b的图象是一条直线，因此我们把一次函数y=kx+b的图象叫做直线y=kx+b 。这条直线与y轴相交于点(0,b)，这里b叫做直线y=kx+b在轴上的截距，简称截距由于两点确定一条直线，所以画一次函数y=kx+b的图象时，我们只需确定直线上任意两点，然后过这两点画一条直线就行了。
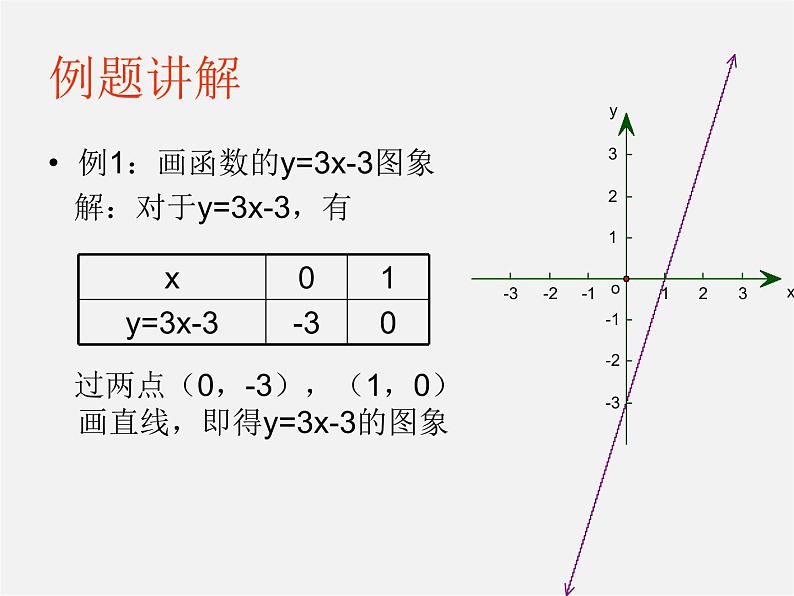
例1：画函数的y=3x-3图象 解：对于y=3x-3，有 过两点（0，-3），（1，0）画直线，即得y=3x-3的图象
在一次函数y=kx+b中，如b=0，可写成y=kx(k≠0) 这时称y是x的正比例函数 因此正比例函数是一次函数的特殊情况
一次函数y=kx+b的图象经过哪几个象限? 当k>0,b>0时，y=kx+b的图象经过一、二、三象限.当k>0,b=0时，y=kx+b的图象经过一、三象限.当k>0,b<0时，y=kx+b的图象经过一、三、四象限.当k<0,b>0时，y=kx+b的图象经过一、二、四象限.当k<0,b=0时，y=kx+b的图象经过二、四象限.当k<0,b<0时， y=kx+b的图象经过二、三、四象限.
1.在画有函数y=2x+3与y=-2x-2的图象的坐标系里，再分别画出函数y=2x,y=-2x的图象2.把两个函数y=2x,y=-2x的图象分别与y=2x+3、y=-2x-2的图象比较，它们之间有什么联系？
直线y=kx+b可以看作是由直线y=kx平移 个单位长度而得到（当时b>0，向上平移；当b<0时，向下平移）
1.已知一次函数 分别列出的对应值表，观察当自变量的值由小到大增加时，函数的值是增加还是减小？ 画出函数图象，上述变化从图象上看，直线从左 到右是上升还是下降 2.用类似的方法，观察函数 图象的变化趋势，从中你发现什么
一般地,一次函数y=kx+b有下列性质: 当k>0时,y随x的增大而增大.图象是自左向右上升的直线. 当k<0时,y随x的增大而减小.图象是自左向右下降的直线.
例2：如果知道一个一次函数，当自变量x=2时，函数值y=4，当x=4,y=2时。写出这个函数的解析式并画出图象。 解：因为是的一次函数，设其解析式为:y=kx+b 由题意，得：2k+b=4 4k+b=2 解方程组，得 k=-1,b=6 所以，函数的解析式是：y=-x+6
这里，先设所求的一次函数关系式为y=kx+b（k,b是待定的系数），再根据已知的条件列出关于k,b的方程组，求得k,b的值.这种确定关系式中系数的方法，叫做待定系数法