初中数学浙教版八年级下册4.6 反证法授课课件ppt

这是一份初中数学浙教版八年级下册4.6 反证法授课课件ppt，共13页。PPT课件主要包含了6反证法，假设李子是甜的，发现知识，不都是，不大于，不小于，一个也没有，至少有两个，至多有n-1个，至少有n+1个等内容，欢迎下载使用。

那么李子会被过路人摘去解渴，树上的李子会很少。
事实上树上的李子很多,这与事实相矛盾。
造成矛盾的原因是：假设李子是甜的，这个假设是错误的，说明原来的结论：路边的李子是苦的是正确的。
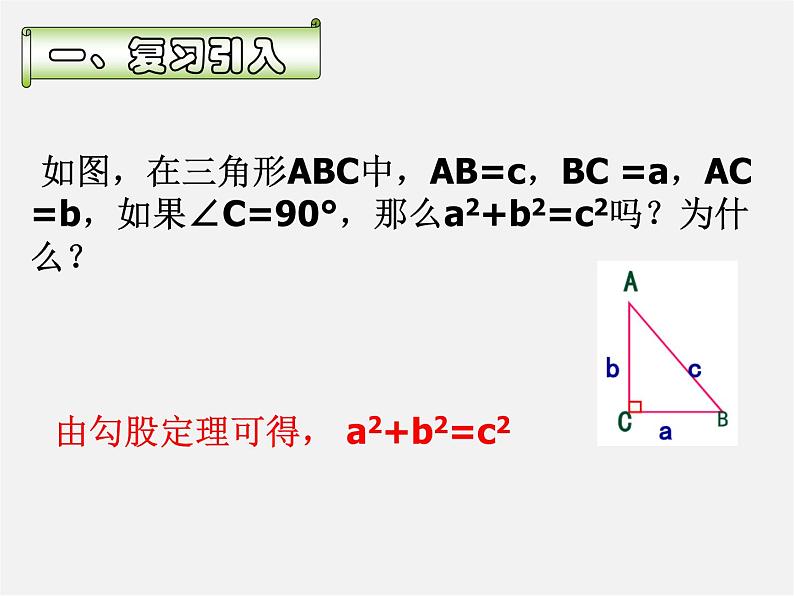
如图，在三角形ABC中，AB=c，BC =a，AC =b，如果∠C=90°，那么a2+b2=c2吗？为什么？
由勾股定理可得， a2+b2=c2
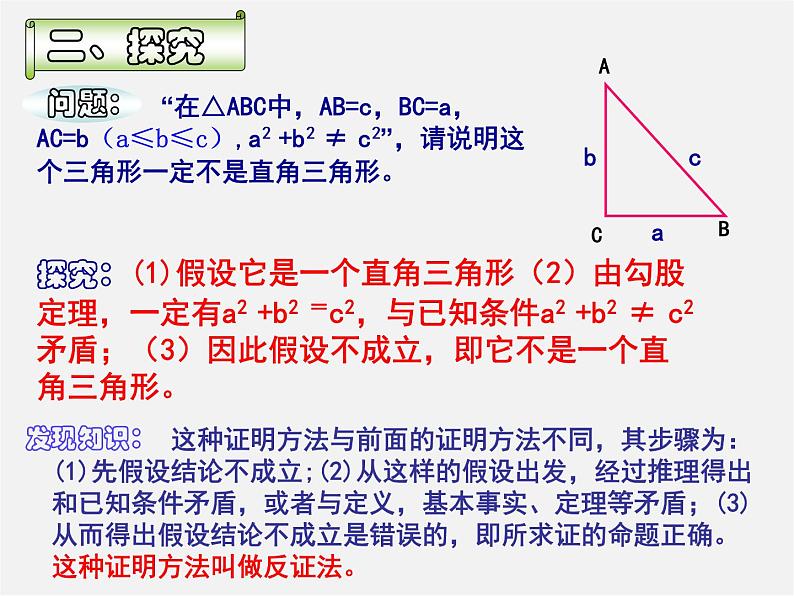
探究：(1)假设它是一个直角三角形（2）由勾股定理，一定有a2 +b2 ＝c2，与已知条件a2 +b2 ≠ c2矛盾；（3）因此假设不成立，即它不是一个直角三角形。
这种证明方法与前面的证明方法不同，其步骤为：(1)先假设结论不成立;(2)从这样的假设出发，经过推理得出和已知条件矛盾，或者与定义，基本事实、定理等矛盾；(3)从而得出假设结论不成立是错误的，即所求证的命题正确。这种证明方法叫做反证法。
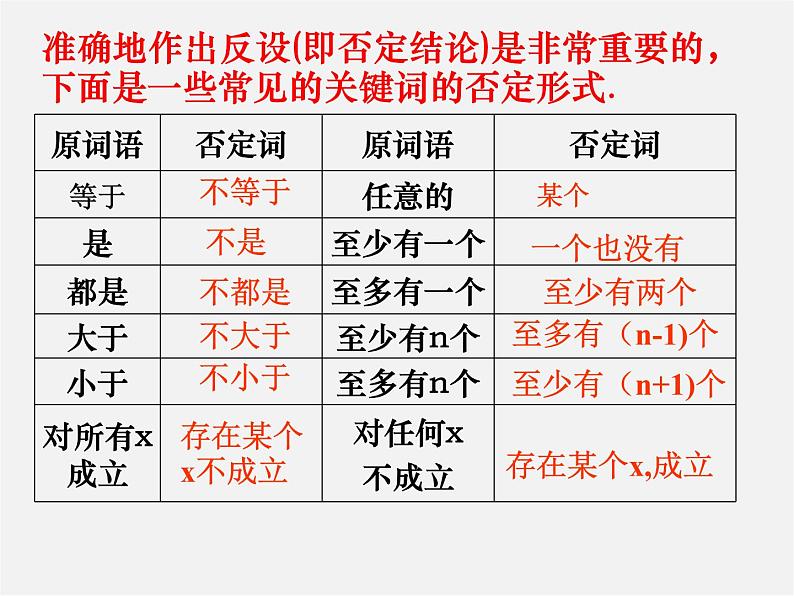
准确地作出反设(即否定结论)是非常重要的，下面是一些常见的关键词的否定形式.  
在△ABC中，若AB≠AC， 则∠B≠∠C.如何说明呢？
那么AB=AC，这与已知条件AB≠AC相矛盾
假设不正确，则∠B≠∠C
假设不正确，则李子是苦的。
那么李子会被过路人摘去解渴,则李子会很少，这与事实相矛盾。
证明：假设a与b不止一个交点，不妨假设有两个交点A和A’。
小结：根据假设推出结论除了可以与已知条件矛盾以外，还可以与我们学过的基本事实、定理矛盾
求证：两条直线相交只有一个交点。
已知：两条相交直线a、b。求证：a与b只有一个交点。
因为两点确定一条直线，即经过点A和A'的直线有且只有一条，这与已知两条直线矛盾,假设不成立。 所以两条直线相交只有一个交点。
证明：假设a与b不平行，则可设它们相交于点A。 那么过点A 就有两条直线a、b与直线c平行，这与“过直线外一点有且只有一条直线与已知直线平行矛盾,假设不成立。 　　∴a//b.
小结：根据假设推出结论除了可以与已知条件矛盾以外，还可以与我们学过的定理、公理矛盾
求证：在一个三角形中，至少有一个内角小于或等于60°。
已知：△ABC求证：△ABC中至少有一个内角小于或等于60°.
证明：假设　　　　　　　　　　　　　　　　　，即　　　　　　　　　　　　　　　　　　　　　。∴　　　　　　　　　　 　　　　，这与　　　　　　　　　　　矛盾．∴　　　　　　　　　　　　　　　　　　　　．∴　　　　　　　　　　　　　　　　　　　　．
△ABC中三个内角都大于60°
∠A>60°,∠B>60°,∠C>60°
三角形的内角和为180度
点拨：至少的反面是没有！
∠A+∠B+∠C>180°
△ABC中至少有一个内角小于或等于60°.