2020-2021初二（上）10月月考数学试卷1

这是一份2020-2021初二（上）10月月考数学试卷1，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


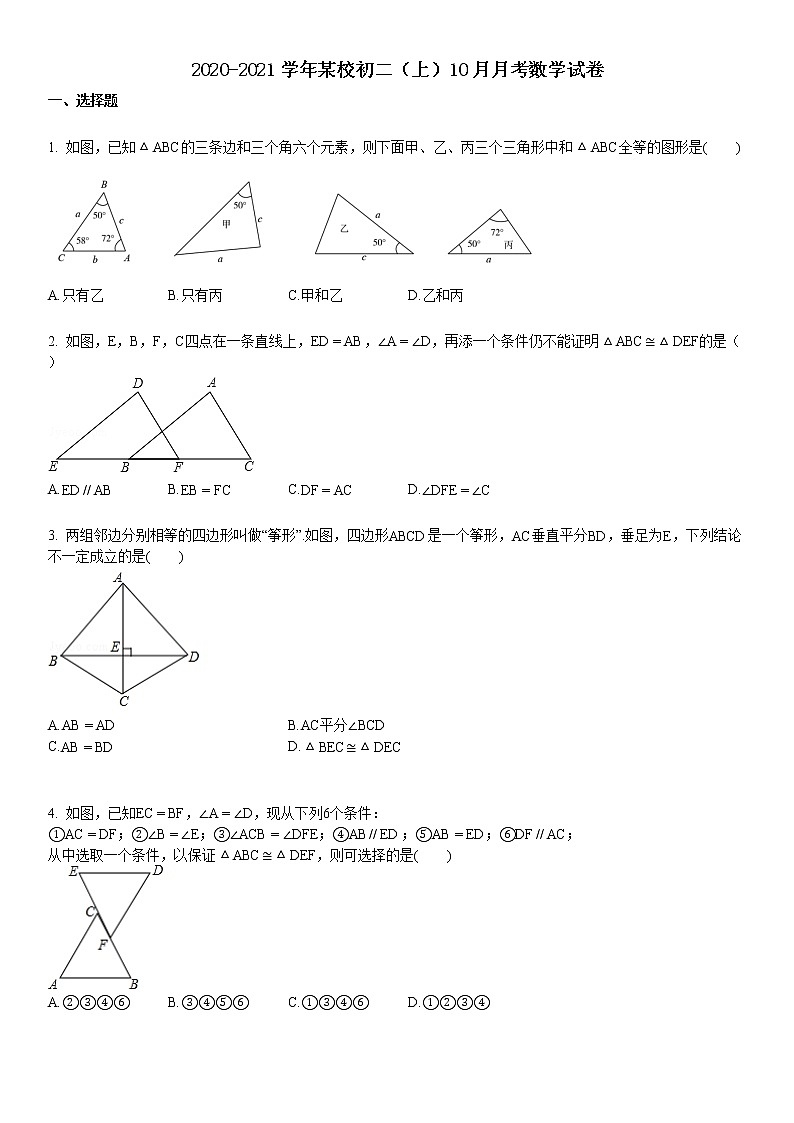
1. 如图，已知△ABC的三条边和三个角六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )

A.只有乙B.只有丙C.甲和乙D.乙和丙

2. 如图，E，B，F，C四点在一条直线上，ED=AB，∠A=∠D，再添一个条件仍不能证明△ABC≅△DEF的是（ ）

A.ED // ABB.EB=FCC.DF=ACD.∠DFE=∠C

3. 两组邻边分别相等的四边形叫做“筝形”.如图，四边形ABCD是一个筝形，AC垂直平分BD，垂足为E，下列结论不一定成立的是( )

A.AB=ADB.AC平分∠BCD
C.AB=BDD.△BEC≅△DEC

4. 如图，已知EC=BF，∠A=∠D，现从下列6个条件：
①AC=DF；②∠B=∠E；③∠ACB=∠DFE；④AB // ED；⑤AB=ED；⑥DF // AC；
从中选取一个条件，以保证△ABC≅△DEF，则可选择的是( )

A.②③④⑥B.③④⑤⑥C.①③④⑥D.①②③④

5. 如图，在△ABC中， ∠C=90∘, DE⊥AB于点E， CD=DE，∠CBD=26∘，则∠A的度数为（ ）

A.40∘B.34∘C.36∘D.38∘

6. 如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，已知EH=EB=3，AE=4，则CH的长是（ ）

A.4B.5C.1D.2

7. 如图，在△ABC中，P，Q分别是BC，AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R，S，若AQ=PQ，PR=PS，则这四个结论中正确的有（ ）
①PA平分∠BAC；②AS=AR；③QP // AR；④△BRP≅△CSP．

A.4个B.3个C.2个D.1个
二、填空题

如图，△ABC≅△ADE，且∠EAB=120∘，∠B=30∘，∠CAD=10∘，则∠CFD=________​∘．


如图，已知△ABC中，∠ABC=90∘，AB=BC，点A，B分别是x轴和y轴上的一动点．当OA=5，OB=2时，求点C的坐标为________


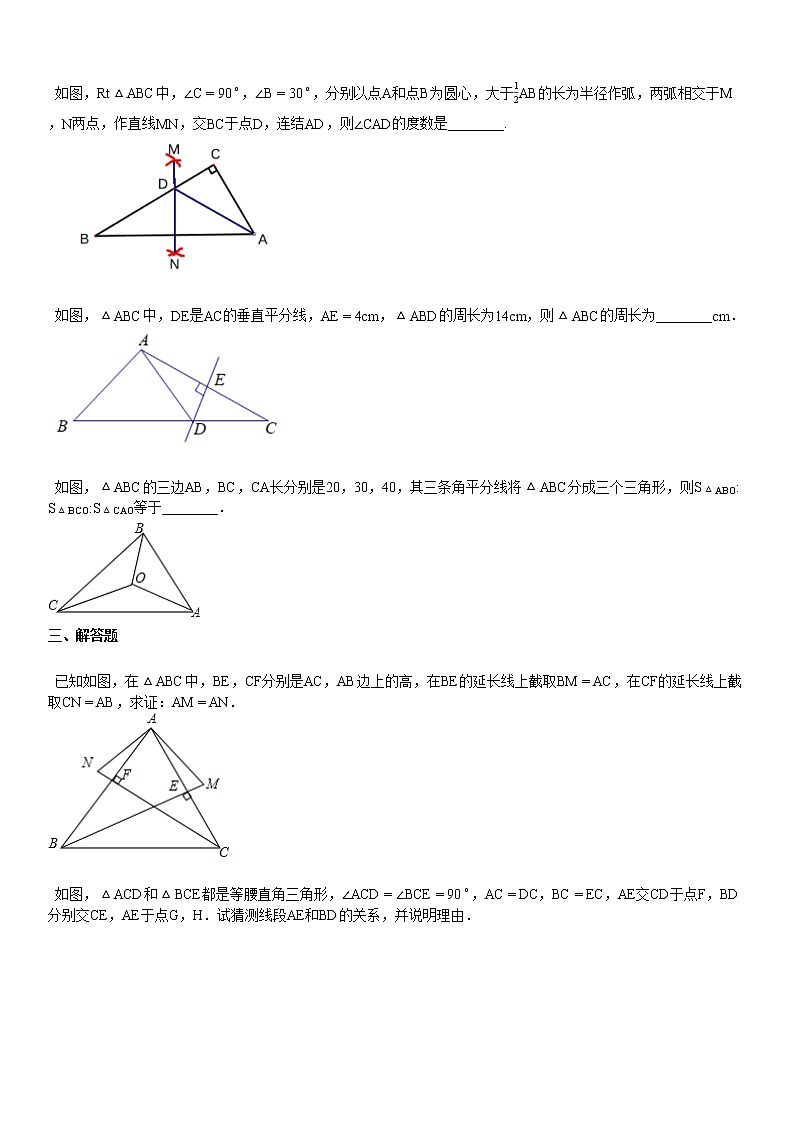
如图，Rt△ABC中，∠C=90∘，∠B=30∘，分别以点A和点B为圆心，大于12AB的长为半径作弧，两弧相交于M，N两点，作直线MN，交BC于点D，连结AD，则∠CAD的度数是________.


如图，△ABC中，DE是AC的垂直平分线，AE=4cm，△ABD的周长为14cm，则△ABC的周长为________cm．


如图，△ABC的三边AB，BC，CA长分别是20，30，40，其三条角平分线将△ABC分成三个三角形，则S△ABO:S△BCO:S△CAO等于________．

三、解答题

已知如图，在△ABC中，BE，CF分别是AC，AB边上的高，在BE的延长线上截取BM=AC，在CF的延长线上截取CN=AB，求证：AM=AN．


如图，△ACD和△BCE都是等腰直角三角形，∠ACD=∠BCE=90∘，AC=DC，BC=EC，AE交CD于点F，BD分别交CE，AE于点G，H．试猜测线段AE和BD的关系，并说明理由．


如图，已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E，EF⊥AB交AB的延长线于点F， EG⊥AC交AC于点G．

(1)求证：BF=CG；

(2)若AB=8，AC=12，求AF的长．

如图1，在平面直角坐标系中，AB⊥x轴于B，AC⊥y轴于C，点C(0, m)，A(n, m)，且(m−4)2+n−4=0，过C点作∠ECF分别交线段AB，OB于E，F两点．

(1)求A点的坐标；

(2)如图1，若OF+BE=AB，求证：CF=CE；

(3)如图2，若∠ECF=45∘，给出两个结论：OF+AE−EF的值不变；OF+AE+EF的值不变，其中有且只有一个结论正确，请你判断出正确的结论，并加以证明和求出其值．
参考答案与试题解析
2020-2021学年湖北省荆州市某校初二（上）10月月考数学试卷
一、选择题
1.
【答案】
D
【考点】
全等三角形的判定
【解析】
分别利用全等三角形的判定方法逐个判断即可．
【解答】
解：在△ABC中，边a，c的夹角为50∘，
∴ 与乙图中的三角形满足SAS，可知两三角形全等，
在丙图中，由三角形内角和可求得另一个角为58∘，且58∘角和50∘角的夹边为a，
∴ △ABC和丙图中的三角形满足ASA，可知两三角形全等，
在甲图中，50∘角的对边为a，可知两三角形不全等，
综上可知能和△ABC全等的是乙、丙.
故选D．
2.
【答案】
B
【考点】
全等三角形的判定
【解析】
根据全等三角形的判定定理分别进行分析即可．
【解答】
解：A，添加ED // AB可得∠E=∠ABC，可利用ASA判定△ABC≅△DEF，故此选项不合题意；
B，由EB=FC可得EF=BC，不能判定△ABC≅△DEF，故此选项符合题意；
C，添加DF=AC可利用SAS判定△ABC≅△DEF，故此选项不合题意；
D，添加∠DFE=∠C可利用AAS判定△ABC≅△DEF，故此选项不合题意.
故选B.
3.
【答案】
C
【考点】
全等三角形的性质与判定
线段垂直平分线的性质
【解析】
此题暂无解析
【解答】
解：∵ AC垂直平分BD，
∴ AB=AD，BC=CD，
∴ AC平分∠BCD，EB=ED，
∴ ∠BCE=∠DCE.
在Rt△BCE和Rt△DCE中，
BE=DE,BC=DC,
∴ Rt△BCE≅Rt△DCE(HL).
故选C.
4.
【答案】
A
【考点】
全等三角形的判定
【解析】
根据全等三角形的判定定理，添上①，没有ASS；添上②，根据AAS可证明；添上③，根据AAS可证明；添上④，根据AAS可证明；添上⑤，没有ASS；添上⑥，根据AAS可证明，正确的有②③④⑥．
【解答】
解：∵ EC=BF，∴ BC=EF.
∵ ∠A=∠D，∠B=∠E，
∴ △ABC≅△DEF(AAS)，故②可以；
∵ ∠A=∠D，∠ACB=∠DFE，BC=EF，
∴ △ABC≅△DEF(AAS)，故③可以；
∵ AB // ED，
∴ ∠B=∠E，
∴ △ABC≅△DEF(AAS)，故④可以；
∵ DF // AC，∴ ∠ACB=∠DFE，
∴ △ABC≅△DEF(AAS)，故⑥可以.
而①⑤不可以．
故选A．
5.
【答案】
D
【考点】
三角形内角和定理
角平分线性质定理的逆定理
【解析】
根据角平分线的判定判断出BD是∠ABC的角平分线，即可得到∠ABD=∠CBD=26∘，再根据三角形的内角和定理即可求得∠A的度数.
【解答】
解：∵ 在△ABC中，∠C=90∘，
∴ CD⊥BC.
∵ DE⊥AB，CD=DE，
∴ BD是∠ABC的角平分线，
∴ ∠ABD=∠CBD.
∵ ∠CBD=26∘，
∴ ∠ABD=26∘，
∴ ∠A=180∘−26∘−26∘−90∘=38∘.
故选D.
6.
【答案】
C
【考点】
全等三角形的性质与判定
【解析】
由AD垂直于BC，CE垂直于AB，利用垂直的定义得到一对角为直角，再由一对对顶角相等，利用三角形的内角和定理得到一对角相等，再由一对直角相等，以及一对边相等，利用AAS得到三角形AEH与三角形EBC全等，由全等三角形的对应边相等得到AE=EC，由EC−EH，即AE−EH即可求出HC的长．
【解答】
解：∵ AD⊥BC，CE⊥AB，
∴ ∠ADB=∠AEH=90∘.
∵ ∠AHE=∠CHD，
∴ ∠BAD=∠BCE，
∵ 在△HEA和△BEC中，
∠EAH=∠BCE,∠AEH=∠BEC=90∘,EH=EB,
∴ △HEA≅△BEC(AAS)，
∴ AE=EC=4，
则CH=EC−EH=AE−EH=4−3=1．
故选C.
7.
【答案】
B
【考点】
全等三角形的性质
【解析】
根据已知条件利用HL易证△APR≅△APS，再利用全等三角形的性质可得∠PAR=∠PAS，AR=AS，从而可证(1)、(2)正确；由AQ=PQ，利用等边对等角易得∠1=∠APQ，再利用三角形外角的性质可得∠PQC=2∠1，而(1)中PA是∠BAC的角平分线可得∠BAC=2∠1，等量代换，从而有∠PQC=∠BAC，利用同位角相等两直线平行可得QP // AR，(3)正确；根据已知条件可知△BRP与△CSP只有一角、一边对应相等，故不能证明两三角形全等，因此(4)不正确．
【解答】
解：①∵ PR⊥AB，PS⊥AC，PR=PS，AP=AP，
∴ △APR≅△APS，
∴ ∠PAR=∠PAS，
∴ PA平分∠BAC；
②由①中的全等也可得AS=AR；
③如图：
∵ AQ= PQ，
∴ ∠1=∠APQ，
∴ ∠PQS=∠1+∠APQ=2∠1，
又∵ PA平分∠BAC，
∴ ∠BAC=2∠1，
∴ ∠PQS=∠BAC，
∴ PQ // AR；
④∵ PR⊥AB，PS⊥AC，
∴ ∠BRP=∠CSP，
∵ PR=PS，
∴ △BRP不一定全等与△CSP（只具备一角一边的两三角形不一定全等）．
故选B．
二、填空题
【答案】
95
【考点】
三角形内角和定理
全等三角形的性质
【解析】
根据全等三角形的性质求出∠BAC的度数，根据三角形内角和定理计算即可．
【解答】
解：∵ △ABC≅△ADE，
∴ ∠BAC=∠DAE=(120∘−10∘)÷2=55∘，
∴ ∠ACF=∠BAC+∠B=85∘，
∴ ∠CFA=180∘−∠ACF−∠CAD=85∘，
∴ ∠CFD=180∘−85∘=95∘.
故答案为：95∘.
【答案】
−2，3
【考点】
全等三角形的性质与判定
【解析】
作CD⊥y轴于D，则可求出∠AOB=∠CDB=90∘， ∠CBM=∠BAO， 证△△BAO≅△CBD， 求出CD=OB=2；再求出BD的长度，最后由OD=BD−OB=3，即可得到答案.
【解答】
解：作CD⊥y轴于点D，
∵ ∠CBD+∠OBA=90∘，∠OBA+∠BAO=90∘，
∴ ∠CBD=∠BAO.
在△BAO和△CBD中，
∠CDB=∠BOA=90∘,∠CBD=∠BAO,BC=AB,
∴ △BAO≅△CBD(AAS)，
∴ CD=OB，DB=OA，
∵ OB=2，∴ CD=2.
∵ OB=2，OA=5，
∴ OD=BD−OB=OA−OB=5−2=3，
∴ 点C的坐标为−2，3.
故答案为：−2，3.
【答案】
30∘
【考点】
作图—基本作图
线段垂直平分线的性质
【解析】
根据内角和定理求得∠BAC=60∘，由垂直平分线性质知DA=DB，即∠DAB=∠B=30∘，从而得出答案．
【解答】
解：在△ABC中，∵ ∠B=30∘，∠C=90∘，
∴ ∠BAC=180∘−∠B−∠C=60∘.
由作图可知MN为AB的垂直平分线，
∴ DA=DB，
∴ ∠DAB=∠B=30∘，
∴ ∠CAD=∠BAC−∠DAB=30∘.
故答案为：30∘.
【答案】
22
【考点】
线段垂直平分线的性质
【解析】
根据线段的垂直平分线的性质得到DA=DC，AE=EC=4cm，由AB+BD+AD=14cm，得到AB+BD+DC=14cm，所以有AB+BC+AC=14cm+8cm=22cm，从而得到结论．
【解答】
解：∵ DE是AC的垂直平分线，
∴ DA=DC，AE=EC=4cm，
而△ABD的周长为14cm，即AB+BD+AD=14cm，
∴ AB+BD+DC=14cm，
∴ AB+BC+AC=14cm+8cm=22cm，
即△ABC的周长为22cm．
故答案为：22．
【答案】
2:3:4
【考点】
三角形的面积
角平分线的性质
【解析】
由角平分线的性质可得，点O到三角形三边的距离相等，即三个三角形的AB、BC、CA的高相等，利用面积公式即可求解．
【解答】
解：过点O作OD⊥AC于D，OE⊥AB于E，OF⊥BC于F.
∵ O是三角形三条角平分线的交点，
∴ OD=OE=OF.
∵ AB=20，BC=30，AC=40，
∴ S△ABO:S△BCO:S△CAO=2:3:4．
故答案为：2:3:4．
三、解答题
【答案】
证明：∵ CF⊥AB，BE⊥AC，
∴ ∠AEB=∠AFC=90∘，
∴ ∠ABE=∠ACF=90∘−∠BAC，
在△AMB和△ANC中，
BM=AC,∠ABE=∠ACF,AB=CN,
∴ △AMB≅△NAC(SAS)，
∴ AM=AN.
【考点】
全等三角形的性质
【解析】
（1）欲证明AM=AN，只要证明AMB≅△NAC即可．
【解答】
证明：∵ CF⊥AB，BE⊥AC，
∴ ∠AEB=∠AFC=90∘，
∴ ∠ABE=∠ACF=90∘−∠BAC，
在△AMB和△ANC中，
BM=AC,∠ABE=∠ACF,AB=CN,
∴ △AMB≅△NAC(SAS)，
∴ AM=AN.
【答案】
解：猜测AE=BD，AE⊥BD.
理由如下：
∵ ∠ACD=∠BCE=90∘，
∴ ∠ACD+∠DCE=∠BCE+∠DCE，
即∠ACE=∠DCB，
∴ 在△ACE与△DCB中，
AC=DC，∠ACE=∠DCB，EC=BC，
∴ △ACE≅△DCB(SAS)，
∴ AE=BD，∠CAE=∠CDB；
∵ ∠AFC=∠DFH，∠FAC+∠AFC=90∘，
∴ ∠DFH+∠FDH=90∘，
∴ ∠DHF=∠ACD=90∘，
∴ AE⊥BD．
故AE=BD，AE⊥BD.
【考点】
全等三角形的性质与判定
等腰直角三角形
【解析】
由于条件可知CD=AC，BC=CE，且可求得∠ACE=∠DCB，所以△ACE≅△DCB，即AE=BD，∠CAE=∠CDB；又因为对顶角相等即∠AFC=∠DFH，所以∠DHF=∠ACD=90∘，即AE⊥BD．
【解答】
解：猜测AE=BD，AE⊥BD.
理由如下：
∵ ∠ACD=∠BCE=90∘，
∴ ∠ACD+∠DCE=∠BCE+∠DCE，
即∠ACE=∠DCB，
∴ 在△ACE与△DCB中，
AC=DC，∠ACE=∠DCB，EC=BC，
∴ △ACE≅△DCB(SAS)，
∴ AE=BD，∠CAE=∠CDB；
∵ ∠AFC=∠DFH，∠FAC+∠AFC=90∘，
∴ ∠DFH+∠FDH=90∘，
∴ ∠DHF=∠ACD=90∘，
∴ AE⊥BD．
故AE=BD，AE⊥BD.
【答案】
(1)证明：连结BE，CE，如图，
∵AE平分∠BAC，EF⊥AB，EG⊥AC，
∴EF=EG.
∵DE垂直平分BC，
∴EB=EC，
在Rt△EFB和Rt△EGC中，EF=EG,EB=EC,
∴Rt△EFB≅Rt△EGC(HL)，
∴BF=CG．
(2)解：∵BF=CG，
∴AB+AC=AB+BF+AG=AF+AG.
又易证Rt△AEF≅Rt△AEG(HL)，
∴AF=AG，
∴AF=12(AB+AC)=10．
【考点】
全等三角形的性质与判定
线段垂直平分线的性质
角平分线的性质
【解析】
左侧图片未给出解析．
左侧图片未给出解析．
【解答】
(1)证明：连结BE，CE，如图，
∵AE平分∠BAC，EF⊥AB，EG⊥AC，
∴EF=EG.
∵DE垂直平分BC，
∴EB=EC，
在Rt△EFB和Rt△EGC中，EF=EG,EB=EC,
∴Rt△EFB≅Rt△EGC(HL)，
∴BF=CG．
(2)解：∵BF=CG，
∴AB+AC=AB+BF+AG=AF+AG.
又易证Rt△AEF≅Rt△AEG(HL)，
∴AF=AG，
∴AF=12(AB+AC)=10．
【答案】
(1)解：(m−4)2+n−4=0，
则m−4=0，n−4=0，
解得：m=4，n=4．
则A的坐标是(4, 4).
(2)证明：∵ AB⊥x轴，AC⊥y轴，A(4, 4)，
∴ AB=AC=OC=OB，∠ACO=∠COB=∠ABO=90∘.
又∵ 四边形的内角和是360∘，
∴ ∠A=90∘.
∵ OF+BE=AB=BE+AE，
∴ AE=OF.
∴ 在△COF和△CAE中，AE=OF,∠A=∠COF,AC=OC,
∴ △COF≅△CAE(SAS)，
∴ CF=CE.
(3)解：结论OF+AE−EF的值不变正确，值为0．
证明：在x轴负半轴上取点H，使OH=AE，
∵ 在△ACE和△OCH中，OH=AE，∠COH=∠A，AC=OC，
∴ △ACE≅△OCH(SAS)，
∴ ∠1=∠2，CH=CE.
又∵ ∠ECF=45∘，
∴ ∠HCF=∠2+∠OCF=∠1+∠OCF=45∘，
∴ 在△HCF和△ECF中，CH=CE,∠HCF=∠ECF,CF=CF,
∴ △HCF≅△ECF(SAS)，
∴ HF=EF，
∴ OF+AE−EF=0．
【考点】
全等三角形的性质与判定
非负数的性质：偶次方
非负数的性质：算术平方根
【解析】
（1）已知的式子可以化成(m−4)2+(n−4)2=0的形式，根据非负数的性质求得m、n的值，即可求得A的坐标；
（2）证明△COF≅△CAE，根据全等三角形的性质即可求解；
（3）在x轴负半轴上取点H，使OH=AE，证明△HCF≅△ECF即可求解．
【解答】
(1)解：(m−4)2+n−4=0，
则m−4=0，n−4=0，
解得：m=4，n=4．
则A的坐标是(4, 4).
(2)证明：∵ AB⊥x轴，AC⊥y轴，A(4, 4)，
∴ AB=AC=OC=OB，∠ACO=∠COB=∠ABO=90∘.
又∵ 四边形的内角和是360∘，
∴ ∠A=90∘.
∵ OF+BE=AB=BE+AE，
∴ AE=OF.
∴ 在△COF和△CAE中，AE=OF,∠A=∠COF,AC=OC,
∴ △COF≅△CAE(SAS)，
∴ CF=CE.
(3)解：结论OF+AE−EF的值不变正确，值为0．
证明：在x轴负半轴上取点H，使OH=AE，
∵ 在△ACE和△OCH中，OH=AE，∠COH=∠A，AC=OC，
∴ △ACE≅△OCH(SAS)，
∴ ∠1=∠2，CH=CE.
又∵ ∠ECF=45∘，
∴ ∠HCF=∠2+∠OCF=∠1+∠OCF=45∘，
∴ 在△HCF和△ECF中，CH=CE,∠HCF=∠ECF,CF=CF,
∴ △HCF≅△ECF(SAS)，
∴ HF=EF，
∴ OF+AE−EF=0．