精品解析：2020年吉林省长春市九台区九年级下学期中考一模数学试题

这是一份精品解析：2020年吉林省长春市九台区九年级下学期中考一模数学试题，文件包含精品解析2020年吉林省长春市九台区九年级下学期中考一模数学试题原卷版doc、精品解析2020年吉林省长春市九台区九年级下学期中考一模数学试题解析版doc等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。

一、选择题（本大题共8小题，每小题3分，共24分）
1. 如图，数轴上蝴蝶所在点表示的数可能为（ ）
A. 3B. 2C. 1D. －1
【答案】D
【解析】
【分析】直接利用数轴得出结果即可．
【详解】解：数轴上蝴蝶所在点表示的数可能为-1，
故选D．
【点睛】本题考查了有理数与数轴上点的关系，任何一个有理数都可以用数轴上的点表示，在数轴上，原点左边的点表示的是负数，原点右边的点表示的是正数，右边的点表示的数比左边的点表示的数大.
2. 今年初，党中央、国务院对湖北发生的新型冠状病毒肺炎疫情非常重视，共派遣援鄂抗役医务人员42000多人，经过全国人民的共同努力，取得了这场战役的胜利：42000这个数用科学记数法表示为( )
A. B. C. D.
【答案】B
【解析】
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．
【详解】解：42000＝4.2×104，
故选：B．
【点睛】此题主要考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3. 某几何体的左视图如图所示，则该几何体不可能是( )
A. B. C. D.
【答案】D
【解析】
【详解】解：几何体的左视图是从左面看几何体所得到的图形，选项A、B、C的左视图均为从左往右正方形个数为2，1，符合题意，选项D的左视图从左往右正方形个数为2，1，1，
故选D．
【点睛】本题考查几何体的三视图．
4. 不等式的解集在数轴上表示正确的是( )
A. B. C. D.
【答案】D
【解析】
【分析】利用不等式的基本性质，移项后再除以2，不等号的方向不变．
【详解】解：移项，得2x≤2，
系数化为1，得x≤1，
不等式的解集在数轴上表示如下：
．
故选：D．
【点睛】本题考查了解一元一次不等式，解不等式要依据不等式基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．
5. 我国古代数学名著《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】设大马有x匹，小马有y匹，根据题意可得等量关系：①大马数+小马数＝100；②大马拉瓦数+小马拉瓦数＝100，根据等量关系列出方程组即可．
详解】解：设大马有x匹，小马有y匹，由题意得：
故选：C．
【点睛】本题考查了二元一次方程组及其应用，首先选取两个量作为未知数，再根据已知条件列出两个方程，再将两个二元一次方程组合起来便构成了二元一次方程组．
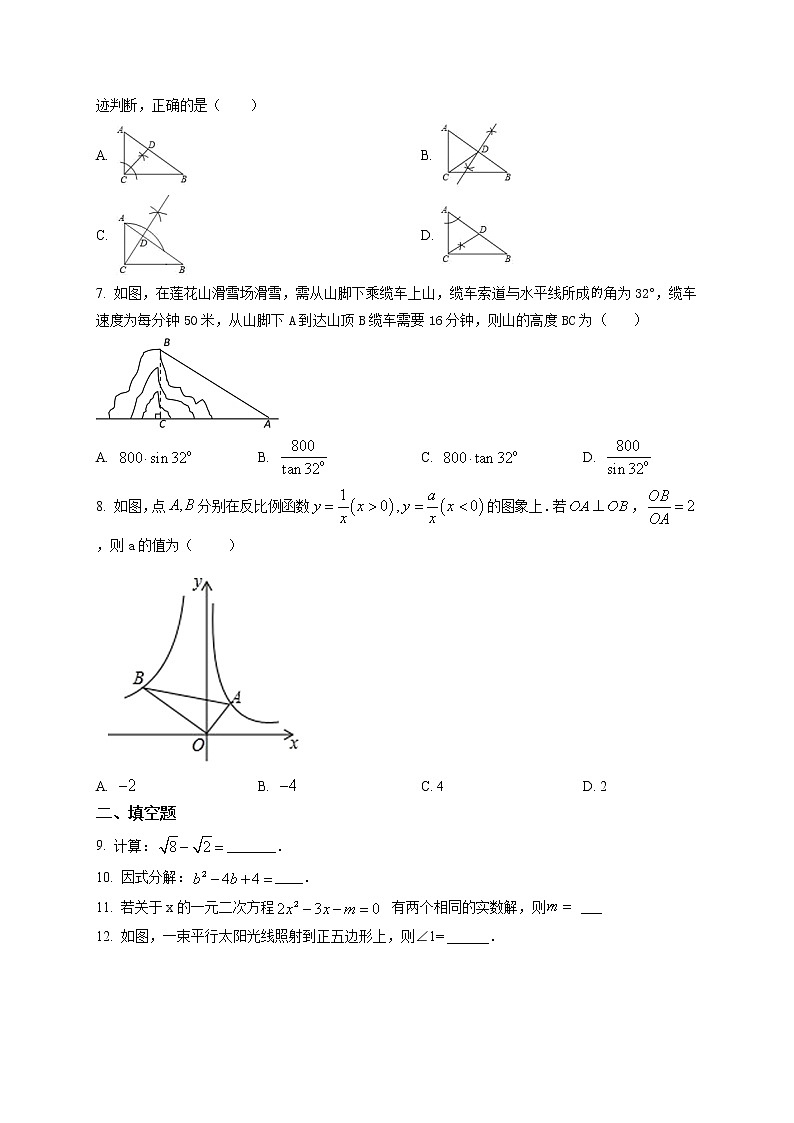
6. 在△ABC中，∠ACB＝90°，用直尺和圆规在AB上确定点D，使△ACD∽△CBD，根据作图痕迹判断，正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】如果∽，可得，即CD是AB的垂线，根据作图痕迹判断即可．
【详解】解：当CD是AB的垂线时，△ACD∽△CBD．
∵CD⊥AB，
∴∠CDA＝∠BDC＝90°，
∵∠ACB＝90°，
∴∠A+∠ACD＝∠ACD+∠BCD＝90°，
∴∠A＝∠BCD，
∴△ACD∽△CBD．
根据作图痕迹可知，
A选项中，CD是∠ACB的角平分线，不符合题意；
B选项中，CD不与AB垂直，不符合题意；
C选项中，CD是AB的垂线，符合题意；
D选项中，CD不与AB垂直，不符合题意；
故选C．
【点睛】本题考查了相似三角形的判定，直角三角形的性质，熟练掌握相似三角形的判定是解题的关键．
7. 如图，在莲花山滑雪场滑雪，需从山脚下乘缆车上山，缆车索道与水平线所成角为32°，缆车速度为每分钟50米，从山脚下A到达山顶B缆车需要16分钟，则山的高度BC为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】作BC⊥AC，垂足为C．在Rt△ABC中，利用三角函数解答即可．
【详解】如图，作BC⊥AC，垂足为C．
在Rt△ABC中，∠ACB=90°，∠BAC=32°，AB=50×16=800，sin∠BAC=，∴BC=AB• sin∠BAC =800•sin32°（米）．
故选A．
【点睛】本题考查了解直角三角形的应用，找到直角三角形并熟悉三角函数的定义是解题的关键．
8. 如图，点分别在反比例函数的图象上．若，，则a的值为（ ）
A. B. C. 4D. 2
【答案】B
【解析】
【分析】分别过点A作AC⊥x轴于C，过点B作BD⊥x轴于D，根据点A所在的图象可设点A的坐标为（x, ），根据相似三角形的判定证出△BDO∽△OCA，列出比例式即可求出点B的坐标，然后代入中即可求出a的值．
【详解】解：分别过点A作AC⊥x轴于C，过点B作BD⊥x轴于D，
∵点A在反比例函数上，
设点A的坐标为（x, ），则OC=x，AC=，
∴∠BDO=∠OCA=90°
∵OA⊥OB，
∴∠BOD＋∠AOC=180°－∠AOB=90°，∠OAC＋∠AOC=90°
∴∠BOD=∠OAC
∴△BDO∽△OCA
∴
解得：OD=2AC=，BD=2OC=2x，
∵点B在第二象限
∴点B的坐标为（，2x）
将点B坐标代入中，解得a=﹣4
故选B．
【点睛】此题考查的是求反比例函数解析式相似三角形的判定及性质，掌握用待定系数法求反比例函数的解析式和构造相似三角形的方法是解决此题的关键．
二、填空题
9. 计算：_______．
【答案】
【解析】
【分析】先把化简为2，再合并同类二次根式即可得解.
【详解】2-=.
故答案为.
【点睛】本题考查了二次根式的运算，正确对二次根式进行化简是关键．
10. 因式分解：____．
【答案】
【解析】
【分析】直接利用完全平方公式进行分解即可．
【详解】解：原式＝，
故答案为：．
【点睛】此题主要考查了用完全平方公式分解因式，解题的关键是熟练掌握完全平方公式．
11. 若关于x的一元二次方程 有两个相同的实数解，则 ___
【答案】
【解析】
【分析】根据一元二次方程的定义和判别式的意义得到△==0，然后解方程即可．
【详解】解：由题意可知△==0
解得：m=
故答案为：．
【点睛】本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了一元二次方程的定义．
12. 如图，一束平行太阳光线照射到正五边形上，则∠1= ______．
【答案】30°．
【解析】
【详解】解：∵AB//CD，∴∠BAC+∠ACD=180°，即∠1+∠EAC+∠ACD=180°，
∵五边形是正五边形，∴∠EAC=108°，
∵∠ACD=42°，∴∠1=180°-42°-108°=30°
故答案为：30°．
13. 图①表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A，当钟面显示3点30分时，分针垂直于桌面，A点距桌面的高度为10cm．图②表示当钟面显示3点45分时，A点距桌面的高度为16cm，若钟面显示3点55分时，A点距桌面的高度为____．
【答案】
【解析】
【分析】根据当钟面显示3点30分时，分针垂直于桌面，A点距桌面的高度为10公分得出AD＝10，进而得出A′C＝16，从而得出FA″＝3，得出答案即可．
【详解】解：∵当钟面显示3点30分时，分针垂直于桌面，A点距桌面的高度为10公分．
∴AD＝10，
∵钟面显示3点45分时，A点距桌面的高度为16公分，
∴A′C＝16，
∴AO＝A″O＝6，
则钟面显示3点55分时，
∠A″OA′＝60°，
在Rt△A″OA′中，sin∠A″OA′＝
∴FA″＝3，
∴A点距桌面的高度为（16+3）公分．
故答案为：16+3．
【点睛】此题主要考查了解直角三角形以及钟面角，得出∠A′OA＝60°，进而得出FA″＝3是解决问题的关键．
14. 如图，在平面直角坐标系中，抛物线与交于点A．过点A作轴的垂线，分别交两条抛物线于点B、C(点B在点A左侧，点C在点A右侧)，则线段BC的长为____．
【答案】6
【解析】
【分析】设抛物线y＝a（x+1）2+b的对称轴与线段BC交于点E，抛物线y＝a（x﹣2）2+b+1的对称轴与线段BC交于点F，由抛物线的对称性可得BC═2（AE+AF），即可求出结论．
【详解】解：设抛物线y＝a（x+1）2+b的对称轴与线段BC交于点E，抛物线y＝a（x﹣2）2+b+1的对称轴与线段BC交于点F，如图所示．

由抛物线的对称性，可知：BE＝AE，CF＝AF，
∵抛物线y＝a（x+1）2+b的对称轴为直线x＝﹣1，抛物线y＝a（x﹣2）2+b+1的对称轴为直线x＝2，
∴BC＝BE+AE+AF+CF＝2（AE+AF）＝2×[2﹣（﹣1）]＝6．
故答案为：6．
【点睛】本题考查了二次函数的性质，利用二次函数图象的对称性解决问题是解题的关键．
三、解答题（本大题共10小题，共78分）
15. 先化简，再求值，其中．
【答案】；15
【解析】
【分析】原式去括号合并得到最简结果，将a的值代入计算即可求出值；
【详解】解：原式
当时，原式
【点睛】本题考查了整式加减-化简求值，涉及的知识有：去括号法则，以及合并同类项法则，熟练掌握运算法则是解题的关键．
16. 在一个不透明的盒子中装有三张卡片，分别标有数字为1，2，7，这些卡片除数字不同外其余均相同，洗匀后，小强从盒子中随机抽取一张卡片记下数字后放回，洗匀后再随机抽取一张卡片，用画树状图或列表的方法，求两次抽取的卡片上数字之和为偶数的概率.
【答案】．
【解析】
【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次抽取的卡片上数字之和是奇数的情况，再利用概率公式即可求得答案．
【详解】解：画出如下树状图：

所以（两次抽取的卡片上数字之和为偶数）．
17. 今年初，新型冠状病毒肺炎侵袭湖北，武汉是重灾区，某爱心人士两次购买N95口罩支援武汉，第一次花了500000元，第二次花了770000，购买了同样的N95口罩，已知第二次购买的口罩的单价是第一次的1.4倍，且比第一次多购进了10000个，求该爱心人士第一次购进口罩的单价．
【答案】5元/个．
【解析】
【分析】设第一次购进口罩的单价是x元，则第二次购进口罩的单价为1.4x元，根据第二次购买数量比第一次多了10000个，可得出方程，解出即可．
【详解】解：设该爱心人士第一次购进口罩的单价为x元/个，则第二次购进口罩的单价为1.4x元/个．
根据题意得：
解得：
经检验，是原方程的解，且符合题意
答；该爱心人士第一次购进口罩的单价为5元/个．
【点睛】本题考查了分式方程的应用，解答本题的关键是找到等量关系，注意分式方程要检验．
18. 如图，E是的斜边AB上一点，以AE为直径的与边BC相切于点D，交边AC于点F，连结AD．
（1）求证：AD平分．
（2）若，，求的长．
【答案】（1）证明见解析；（2）．
【解析】
【分析】（1）连结OD，由切线的性质及∠C=90°可得OD∥AC，进而得∠CAD=∠ODA，再由OA=OD得∠OAD=∠ODA，等量代换即可得证；
（2）先由∠CAD=25°求得∠EOF=100°，再利用弧长公式计算即可．
【详解】（1）如图，连结OD．
∵⊙O与边BC相切于点D，
∴OD⊥BC，
∴∠ODB=90°．
∵∠C=90°，
∴∠C=∠ODB=90°，
∴OD∥AC，
∴∠CAD=∠ODA．
∵OA=OD，
∴∠OAD=∠ODA，
∴∠OAD=∠CAD．
∴AD平分∠BAC．
（2）如图，连结OF．
∵AD平分∠BAC，且∠CAD=25°，
∴，
∴∠EOF=100°，
∴的长为．
【点睛】本题考查了切线的性质，等腰三角形的性质，弧长公式等知识，熟练掌握切线的性质是解题的关键．
19. 某工厂生产部门为了解本部门工人的生产能力情况，进行了抽样调查．该部门随机抽取了30名工人某天每人加工零件的个数，数据如下：
整理上面数据，得到条形统计图：
样本数据的平均数、众数、中位数如下表所示：
根据以上信息，解答下列问题：
（1）上表中众数m的值为 ；
（2）为调动工人的积极性，该部门根据工人每天加工零件的个数制定了奖励标准，凡达到或超过这个标准的工人将获得奖励．如果想让一半左右的工人能获奖，应根据 来确定奖励标准比较合适．（填“平均数”、“众数”或“中位数”）
（3）该部门规定：每天加工零件的个数达到或超过25个的工人为生产能手．若该部门有300名工人，试估计该部门生产能手的人数．
【答案】(1)18；（2）中位数；（3）100名.
【解析】
【详解】【分析】（1）根据条形统计图中的数据可以得到m的值；
（2）根据题意可知应选择中位数比较合适；
（3）根据统计图中的数据可以计该部门生产能手的人数．
【详解】（1）由图可得，
众数m的值为18，
故答案为18；
（2）由题意可得，
如果想让一半左右的工人能获奖，应根据中位数来确定奖励标准比较合适，
故答案为中位数；
（3）300×=100（名），
答：该部门生产能手有100名工人．
【点睛】本题考查了条形统计图、用样本估计总体、加权平均数、中位数和众数，解答本题的关键是明确题意，利用数形结合的思想解答．
20. 图①，图②，图③均是正方形网格，每个小正方形的项点称为格点，线段的端点均在格点上，在图①，图②，图③恰当的网格中按要求画图.
（1）在图①中，画出格点，使，用黑色实心圆点标出点所有可能的位置.
（2）在图②中，在线段上画出点，使.
（3）在图③中，在线段上画出点，使.（保留作图痕迹）
要求：借助网格，只用无刻度的直尺，不要求写出画法.
【答案】(1)详见解析;(2)详见解析;(3)详见解析
【解析】
【分析】（1）做出AB的垂直平分线，落在垂直平分线上的格点即可；（2）利用相似三角形性质找到M点即可 （3）利用相似三角形相似比找出P点即可
【详解】(1) 如图所示:
(2)如图:
(3)如图:
【点睛】本题考查在方格纸上作图，第二三问的关键在于利用相似三角形找出点
21. 小明在练习操控航拍无人机，该型号无人机在上升和下落时的速度相同，设无人机的飞行高度为y（米），小明操控无人飞机的时间为x（分），y与x之间的函数图象如图所示．
（1）无人机上升的速度为 米/分，无人机在40米的高度上飞行了 分．
（2）求无人机下落过程中，y与x之间的函数关系式．
（3）求无人机距地面的高度为50米时x的值．
【答案】（1）20，3；（2）y=﹣20x+240；（3）无人机距地面的高度为50米时x的值为5.5和9.5．
【解析】
【分析】（1）利用图象信息，根据速度=计算即可解决问题；（2）利用待定系数法即可解决问题；（3）求出无人机从40米高度到60米高度的函数关系式为y=20x-60（5≤x≤6），分两种情形构建方程即可解决问题；
【详解】（1）无人机上升的速度为=20米/分，无人机在40米的高度上飞行了6﹣1﹣2=3分．
故答案为20，3；
（2）设y=kx+b，把（9，60）和（12，0）代入得到，
解得 ，
∴无人机下落过程中，y与x之间的函数关系式为y=﹣20x+240．
（3）易知无人机从40米高度到60米高度的函数关系式为y=20x﹣60（5≤x≤6），
由20x﹣6﹣=50，解得x=5.5，
由﹣2﹣x+240=50，解得x=9.5，
综上所述，无人机距地面的高度为50米时x的值为5.5和9.5．
【点睛】本题考查了一次函数的应用、待定系数法等知识，解题的关键是读懂图象信息，灵活运用所学知识解决问题．
22. 教材呈现：下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形，线段的垂直一部分线是线段的对称轴，如图直线是线段的垂直平分线，是上任一点，连结、，将线段与直线对称，我们发现与完全重合，由此都有：线段垂直平分线的性质定理，线段垂直平分线上的点到线段的距离相等.
已知：如图，，垂足为点，，点是直线上的任意一点.
求证：.
分析：图中的两个直角三角形和，只要证明这两个三角形全等，便可证明（请写出完整的证明过程）
请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程，定理应用.
（1）如图②，在中，直线、、分别是边、、的垂直平分线.
求证：直线、、交于点.
（2）如图③，在中，，边的垂直平分线交于点，边的垂直平分线交于点，若，，则的长为_______.

【答案】教材呈现：详见解析；定理应用：（1）详见解析；（2）6.
【解析】
【分析】教材呈现： 得到，从而
定理应用：（1）连结、、．设直线、交于点．因为直线是边的垂直平分线，所以 又因直线是边的垂直平分线， 得到 点在边的垂直平分线上．得到直线、、交于点． （2）
连接BD，BF，易知AD=DB，BE=EC；又因为∠A=∠C=30°，得到∠DBE=60°，所以∠ABD=30°，得到∠BDE=60°，所以△BED为等边三角形，所以DE=AC=6
【详解】教材呈现：
，

又
．

图① 图②
定理应用：
（1）连结、、．
设直线、交于点．
直线是边的垂直平分线，

又直线是边的垂直平分线，


点在边的垂直平分线上．
直线、、交于点．
（2）如图3，连接BD,BF
由第一问可知，AD=DB，BE=EC，∠A=∠DBA，∠C=∠CBE
∵AB=AC
∴∠A=∠C
∵∠ABC=120°
∴∠A=∠C=30°
∴∠A=∠DBA=∠C=∠CBE=30°
∴∠BDE=∠A+∠ABD=60°，∠DBE=∠ABC-∠ABD-∠EBC=60°
∴△DBE是等边三角形
∴DB=BE=DE
∴AD=DE=EC
∴DE=AC=6
【点睛】本题考查垂直平分线的性质与证明，能够读懂题意给到的方法进行解题是本题关键
23. 在中，，，，点D在边AB上，且，动点P从点A出发，以每秒1个单位长度的速度向终点B运动，以PD为边向上做正方形，设点P运动的时间为秒，正方形与重叠部分的面积为．
（1）用含有的代数式表示线段的长．
（2）当点落在的边上时，求的值．
（3）求与的函数关系式．
（4）当点P在线段AD上运动时，做点N关于CD的对称点，当与的某一个顶点的连线平分的面积时，求的值．
【答案】（1）当0t3时PD=3-t，当3＜t7时，PD=t-3；（2），；（3）；（4），，．
【解析】
【分析】（1）分0＜t≤3时，3＜t≤7时，两种情形分别求解即可．
（2）分两种情形①如图2中，当点N在AC上时，②如图3中，当点N在BC上时，利用平行线分线段成比例定理解决问题即可．
（3）分三种情形：①如图4中，当0＜t≤时，重叠部分是五边形EFPDM，②如图5或6中．当＜t≤5时，重叠部分是正方形PDMN．③如图7中，当5＜t≤7时，重叠部分是五边形EFPDM，分别求解即可．
（4）分三种情形画出图形，利用平行线分线段成比例定理构建方程即可解决问题．
【详解】解：（1）如图1中，作CD′⊥AB于D．

∵∠B＝45°，BC＝4，
∴CD′＝BD′＝4，
又∵CD′⊥AB，，
∴在Rt△ACD′中，
AD′＝，
∵AD＝3，
∴AD＝AD′，
∴D′与D重合，
当0＜t≤3时，PD＝3﹣t．
当3＜t≤7时，PD＝t﹣3．
（2）①如图2中，当点N在AC上时，

∵MN∥AD，
∴，
∴，
解得t＝．
②如图3中，当点N在BC上时，

∵MN∥BD，
∴，
∴，
解得t＝5
综上所述，满足条件的t的值为s或5s．
（3）①如图4中，当0＜t≤时，重叠部分是五边形EFPDM，

s＝S正方形MDPN﹣S△NEF＝（3﹣t）2﹣
②如图5或6中，当＜t≤5时，重叠部分是正方形PDMN，s＝t2﹣6t+9

③如图7中，当5＜t≤7时，重叠部分是五边形EFPDM，s＝S正方形MNPD﹣S△EFN＝（t﹣3）2﹣•[（t﹣3）﹣（7﹣t）]2＝﹣t2+14t﹣41．

综上所述，．
（4）如图8中，当点N′落在中线AE上时，作EK⊥BC于K，N′J⊥AB于J．

∵JN′∥EK，
∴，
则有，
解得t＝1．
如图9中，当点N′落在中线BG上时，作GK⊥BC于K，N′J⊥AB于J．

∵N′J∥GK，
∴，
∴，
解得t＝．
如图10中，当点N′落在中线CF上时，

∵MN′∥DF，
∴，
∴，
解得t＝．
综上所述，满足条件的t的值为1s或s或s．
【点睛】本题属于四边形综合题，考查了解直角三角形，平行线分线段成比例定理，正方形的性质，轴对称等知识，解题的关键是学会用分类讨论的思想思考问题，学会构建方程解决问题，属于中考压轴题．
24. 在平面直角坐标系中，对于点P（x，y）和Q（x，y′），给出如下定义：如果y′＝，那么称点Q为点P的“伴随点”．
例如：点（5，6）的“伴随点”为点（5，6）；点（﹣5，6）的“伴随点”为点（﹣5，﹣6）．
（1）直接写出点A（2，1）的“伴随点”A′的坐标．
（2）点B（m，m+1）在函数y＝kx+3的图象上，若其“伴随点”B′的纵坐标为2，求函数y＝kx+3的解析式．
（3）点C、D在函数y＝﹣x2+4的图象上，且点C、D关于y轴对称，点D的“伴随点”为D′．若点C在第一象限，且CD＝DD′，求此时“伴随点”D′的横坐标．
（4）点E在函数y＝﹣x2+n（﹣1≤x≤2）的图象上，若其“伴随点”E′的纵坐标y′的最大值为m（1≤m≤3），直接写出实数n的取值范围．
【答案】（1）A'的坐标为（2，1）；（2）①当m≥0时，y＝﹣x+3；②m＜0时，y＝x+3；（3）D′的横坐标为；（4）﹣2≤n≤0、1≤n≤3.
【解析】
【分析】（1）由题意即可求解；
（2）分m≥0、m＜0两种情况分别求解即可；
（3）设点C的横坐标为n，点C在函数y＝﹣x2+4的图象上，CD＝DD′，即可求解；
（4）通过画图即可求解．
【详解】解：（1）由题意得：点A'的坐标为（2，1）
（2）①当m≥0时，
m+1＝2，m＝1
∴B（1，2）
∵点B在一次函数y＝kx图象上，
∴k+3＝2，
解得：k＝+1
∴一次函数解析式为y＝﹣x+3
②m＜0时，
m+1＝﹣2，m＝﹣3
∴B（﹣3，﹣2）
∵点B在一次函数y＝kx+3图象上，
∴﹣3k+3＝﹣2
解得：k＝
一次函数解析式为y＝x+3．
（3）设点C的横坐标为n，点C在函数y＝﹣x2+4的图象上，
∴点C的坐标为（n，﹣n2+4），
∴点D的坐标为（﹣n，﹣n2+4），D′（﹣n，n2﹣4）
∵CD＝DD′，
∴2n＝2（n2+4），
解得：n＝；
∵点C在第一象限，
∴D′的横坐标为；
（4）﹣2≤n≤0、1≤n≤3，
当左边的抛物线在上方时，如图①、图②：﹣2≤n≤0；
当右边的抛物线在上方时，如图③、图④：1≤n≤3．
【点睛】本题考查二次函数综合题.在（2）中需要注意伴随点的取值，取决于原函数中x的正负，所以要分情况讨论；（3）时可先结合题意画出y＝﹣x2+4的草图，标记点的大致位置，根据图形分析，需注意C点在第一象限，所以结果中要筛选排除不符合的；（4）分n≥0和n＜0，两种情况画出y＝﹣x2+n的草图，根据草图画伴随点的E'的运动轨迹进行分析.20
21
19
16
27
18
31
29
21
22
25
20
19
22
35
33
19
17
18
29
18
35
22
15
18
18
31
31
19
22
统计量
平均数
众数
中位数
数值
23
m
21