高考数学专项解题方法归纳探究（全国通用）模板12 椭圆与方程（解析版）

学校:___________姓名：___________班级：___________考号：___________

模板一、求椭圆的标准方程

1.模板解决思路

(1)在=1和=1两个方程中都有a>b>0的条件，要分清焦点的位置，只需要看x2和y2的分母的大小.

例如,方程=1(m>0,n>0,m≠n)

当m>n时表示焦点在x轴上的椭圆;当m<n时表示焦点在y轴上的椭圆.

(2)如果椭圆焦点位置不能确定，可设方程

=l(A ,B>0,A≠B)或=1(m2≠n2).

2.模板解决步骤

①第一步作判断:根据条件判断椭圆的焦点在x轴上，还是在y轴上，还是两个坐标轴都有可能

②第二步设方程:根据 上述判断设方程号+6-=1(a>b>0或号告l(ab>)，或设出含其他待定系数的方程.

③第三步找关系:根据已知条件，建立方程(组),求出待定系数.

④第四步得方程:解方程组 ,将解代入所设方程.

知识点一、椭圆的定义

1．定义：平面内与两个定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹．

2．焦点：两个定点F1，F2.

3．焦距：两焦点间的距离|F1F2|.

4．几何表示：|MF1|＋|MF2|＝2a(常数)且2a>|F1F2|.

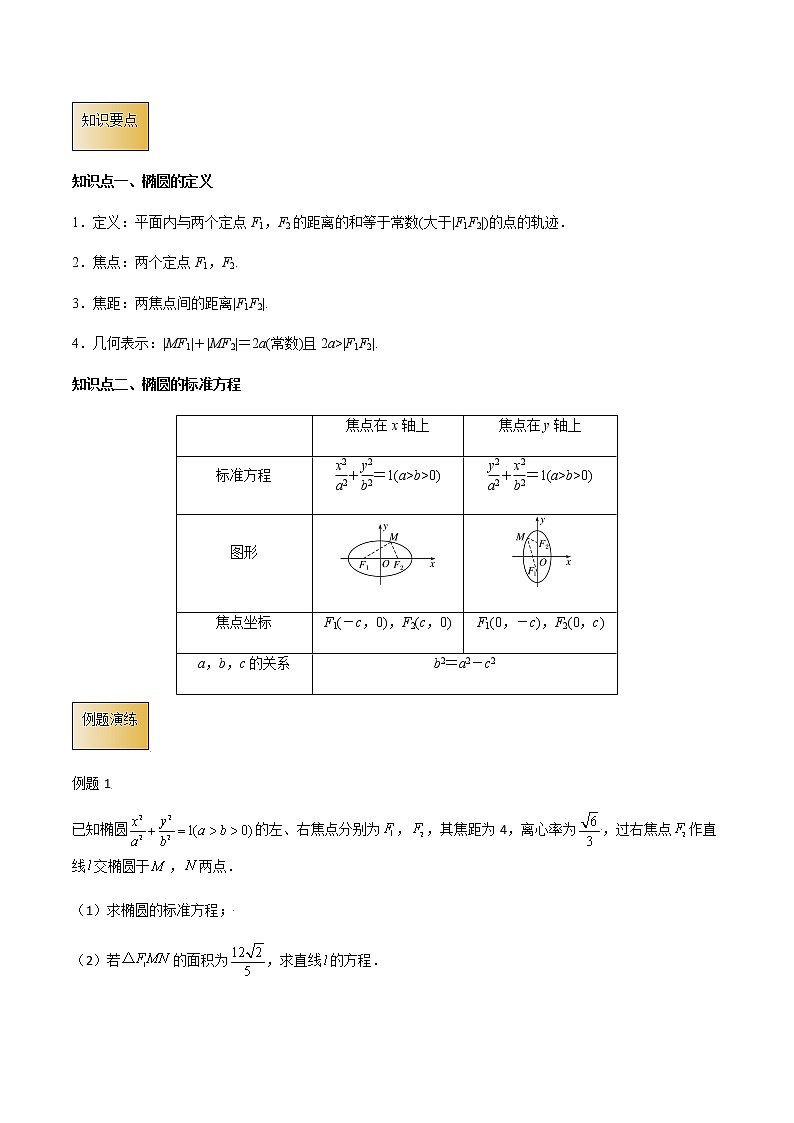
知识点二、椭圆的标准方程

例题1

已知椭圆的左、右焦点分别为，，其焦距为4，离心率为，过右焦点作直线交椭圆于，两点．

（1）求椭圆的标准方程；

（2）若的面积为，求直线的方程．

【答案】（1）；（2）或．

【详解】

（1）根据题意可得，

解得，，

所以椭圆的方程为．

（2）由（1）知，

设直线的方程为，，，

所以，得，

所以，

所以，，

所以

，

解得或，

所以直线的方程为或．

例题2

设椭圆的离心率，焦距为4．

（1）求椭圆的标准方程；

（2）过椭圆右焦点的动直线交椭圆于两点，为直线上的一点，是否存在直线与点P，使得恰好为等边三角形，若存在求出的面积，若不存在说明理由．

【答案】（1）；（2）存在；．

【详解】

解（1）；依题意，

又所以：

椭圆的标准方程为

（2）设直线，联立椭圆方程整理得

记则

所以

记AB中点为，则

要满足题目要求，则需要，

即

所以，经检验均符合愿意．

模板二、求椭圆的离心率

1.模板解决思路

（1）离心率：，也就是说，给出离心率实质是给出了的比值

（2）若点P是椭圆上一点，F1，F2椭圆的两个焦点，由于，而因此可以把其转化到△PF1F2中，利用解三角形的知识来解决离心率问题

2.模板解决步骤

①第一步根据已知条件，得到关于,b,c的关系式或方程(组).

②第二步直接求出 ,c的值;也可根据b2=c2-c2,消去b得到关于,c的方程,并化简.

③第三步求出 的值，即得离心率e.

知识点1.椭圆的简单几何性质

知识点2.求椭圆离心率及取值范围的两种方法

(1)直接法：若已知a，c可直接利用e＝求解．若已知，b或b，c可借助于2＝b2＋c2求出c或，再代入公式e＝求解．

(2)方程法：若，c的值不可求，则可根据条件建立，b，c的关系式，借助于2＝b2＋c2，转化为关于，c的齐次方程或不等式，再将方程或不等式两边同除以的最高次幂，得到关于e的方程或不等式，即可求得e的值或取值范围

例题1

已知椭圆的左､右焦点分别为､，过点的直线交椭圆于两点.

（1）若的周长为，面积的最大值为，求椭圆的标准方程；

（2）设分别为椭圆的左､右顶点，直线，的斜率分别为，若，求椭圆的离心率的取值范围.

【答案】（1）答案见解析；（2）.

【详解】

（1）由椭圆定义得：，所以，

又当点P位于短轴端点时，的面积最大，

此时，即，

又，解得①时，椭圆的标准方程为，

②时，椭圆的标准方程为.

（2）设，，，

由题意知直线斜率不为，且过，设，

联立，整理得，

所以()，且，

由题知，

则有，

将()代入整理得：

所以，

所以

例题2

已知椭圆的右焦点为，点与点是椭圆的顶点，

（1）求椭圆的离心率；

（2）设以离心率为斜率的直线经过点A，与椭圆相交于点P(点不在坐标轴上)，

（i）证明：点在以线段为直径的圆上；

（ii）若，求椭圆的方程.

【答案】（1）；（2）（i）证明见解析；（ii）.

【详解】

（1）在椭圆C中，，，故

（2）（i）由（1）知，，直线l为，设，

联立 ，化简得，

故，又，

所以P与F点横坐标相同，即，

根据直角三角形的性质易知点在以线段为直径的圆上.

（ii）由上述求得坐标即关系知：

，，，，

则

故，

椭圆方程为