

2021-2022学年广东省深圳市龙岗区宝龙学校八年级(上)期中数学试卷 解析版
展开2021-2022学年广东省深圳市龙岗区宝龙学校八年级(上)期中数学试卷
一、选择题(以下各题只有一项正确答案,请将答题卡对应选项涂黑。每小题3分,共30分)
1.(3分)下列实数中,无理数是( )
A.﹣ B.0 C.3.14159 D.
2.(3分)下列计算正确的是( )
A. B. C.3+2=5 D.=2
3.(3分)在平面直角坐标系的第四象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是( )
A.(3,﹣4) B.(﹣4,3) C.(4,﹣3) D.(﹣3,4)
4.(3分)已知点P(x,y),且+|y+4|=0,则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(3分)函数的自变量x的取值范围是( )
A.x≥2 B.x≥3 C.x≠3 D.x≥2且x≠3
6.(3分)△ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是( )
A.a2+b2=c2 B.∠A=∠B+∠C
C.∠A:∠B:∠C=3:4:5 D.a=5,b=12,c=13
7.(3分)若点A(2m,2﹣m)和点B(3+n,n)关于y轴对称,则m、n的值为( )
A.m=1,n=﹣1 B.,
C.m=﹣5,n=7 D.,
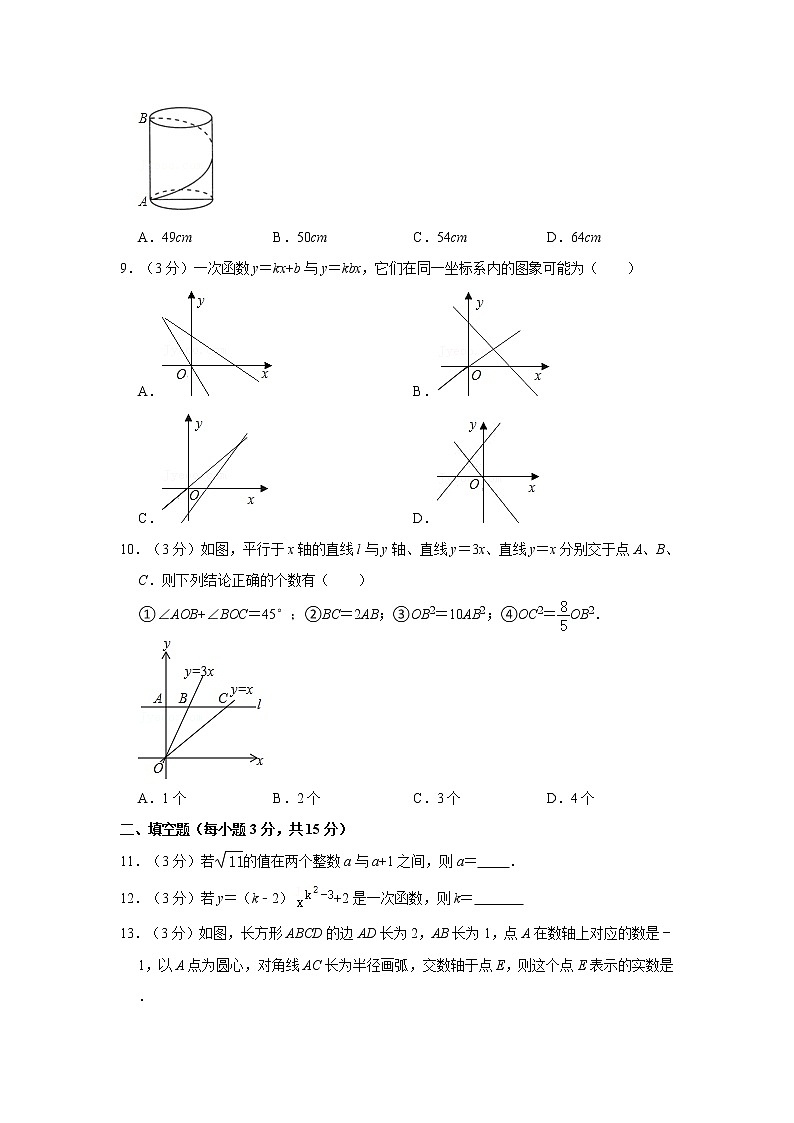
8.(3分)如图,若圆柱的底面周长是14cm,高是48cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.49cm B.50cm C.54cm D.64cm
9.(3分)一次函数y=kx+b与y=kbx,它们在同一坐标系内的图象可能为( )
A. B.
C. D.
10.(3分)如图,平行于x轴的直线l与y轴、直线y=3x、直线y=x分别交于点A、B、C.则下列结论正确的个数有( )
①∠AOB+∠BOC=45°;②BC=2AB;③OB2=10AB2;④OC2=OB2.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11.(3分)若的值在两个整数a与a+1之间,则a= .
12.(3分)若y=(k﹣2)+2是一次函数,则k=
13.(3分)如图,长方形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是﹣1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则这个点E表示的实数是 .
14.(3分)对于任意的正数m、n定义运算※为:m※n=,计算(3※2)×(8※12)的结果为 .
15.(3分)如图,一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为 .
三、解答题(第16题6分、第17题6分、第18题8分、第19题8分、第20题8分、第21题10分、第22题10分,共55分)
16.(6分)计算:(1);
(2).
17.(6分)(1)已知:2a+1的算术平方根是3,3a﹣b﹣1的立方根是2,求的值.
(2)已知10+=x+y,其中x是整数,且0<y<1,求x﹣y+的算术平方根.
18.(8分)如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在图中画出△ABC,△ABC的面积是 ;
(2)若点D与点C关于y轴对称,则点D的坐标为 ;
(3)已知Q为y轴上一点,若△ACQ的面积为8,求点Q的坐标.
19.(8分)为了鼓励居民节约用水,某市采用“阶梯水价”的方法按月计算每户家庭的水费:每月用水量不超过20吨时,按每吨2元计费;每月用水量超过20吨时,其中的20吨仍按每吨2元计费,超过部分按每吨2.8元计费,设每户家庭每月用水量为x吨时,应交水费y元.
(1)分别求出0≤x≤20和x>20时,y与x之间的函数表达式;
(2)小颖家四月份、五月份分别交水费45.6元、38元,问小颖家五月份比四月份节约用水多少吨?
20.(8分)如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,将△ABE沿AE折叠,使点B落在B'处.
(1)若∠CEB'=70°,求∠DAB'.
(2)若点B'恰好在矩形ABCD的对角线AC上,求BE的长.
21.(10分)“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a= ,b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发后至到达图书馆前,何时与小军相距100米,请求出此时小军骑行的时间.(直接写出答案)
22.(10分)如图,在平面直角坐标系中,直线y=﹣2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
(1)求点C的坐标.
(2)若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.
(3)在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.
2021-2022学年广东省深圳市龙岗区宝龙学校八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(以下各题只有一项正确答案,请将答题卡对应选项涂黑。每小题3分,共30分)
1.(3分)下列实数中,无理数是( )
A.﹣ B.0 C.3.14159 D.
【分析】根据无理数的定义(无理数是指无限不循环小数)判断即可.
【解答】解:A、不是无理数,故本选项错误;
B、不是无理数,故本选项错误;
C、不是无理数,故本选项错误;
D、是无理数,故本选项正确;
故选:D.
2.(3分)下列计算正确的是( )
A. B. C.3+2=5 D.=2
【分析】利用二次根式的加减法对A、C进行判断;根据二次根式的乘法法则对C进行判断;根据二次根式的除法法则对D进行判断.
【解答】解:A. 与不能合并,所以A选项不符合题意;
B.原式==,所以B选项符合题意;
C.3与2不能合并,所以C选项不符合题意;
D.原式==,所以D选项不符合题意.
故选:B.
3.(3分)在平面直角坐标系的第四象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是( )
A.(3,﹣4) B.(﹣4,3) C.(4,﹣3) D.(﹣3,4)
【分析】根据点到x轴的距离是纵坐标的绝对值,点到y轴的距离是横坐标的绝对值,根据第四象限内点的横坐标大于零,纵坐标小于零,可得答案.
【解答】解:由点M到x轴的距离为3,到y轴的距离为4,得
|y|=3,|x|=4,
由点位于第四象限,得
y=﹣3,x=4,
点M的坐标为(4,﹣3),
故选:C.
4.(3分)已知点P(x,y),且+|y+4|=0,则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】首先依据非负数的性质确定出x、y的值,然后再确定出所在的象限即可.
【解答】解:∵+|y+4|=0,
∴x=2,y=﹣4.
∴点P在第四象限.
故选:D.
5.(3分)函数的自变量x的取值范围是( )
A.x≥2 B.x≥3 C.x≠3 D.x≥2且x≠3
【分析】本题中,根号内的数大于等于零,分式中,分母不等于零,因此题目中要想使式子有意义,只要有x﹣2≥0且x﹣3≠0,就可以求出x的范围.
【解答】解:根据题意得:x﹣2≥0且x﹣3≠0,
解得:x≥2且x≠3.
故选:D.
6.(3分)△ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是( )
A.a2+b2=c2 B.∠A=∠B+∠C
C.∠A:∠B:∠C=3:4:5 D.a=5,b=12,c=13
【分析】根据勾股定理的逆定理及三角形内角和定理对各选项进行逐一判断即可.
【解答】解:A、∵a2+b2=c2,∴此三角形是直角三角形,故本选项不符合题意;
B、∵∠A+∠B+∠C=180°,∠A=∠B+∠C,
∴∠A=90°,
∴此三角形是直角三角形,故本选项不符合题意;
C、设∠A=3x,则∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,
∴3x+4x+5x=180°,解得x=15°,
∴∠C=5×15°=75°,
∴此三角形不是直角三角形,故本选项符合题意;
D、∵52+122=132,
∴此三角形是直角三角形,故本选项不符合题意;
故选:C.
7.(3分)若点A(2m,2﹣m)和点B(3+n,n)关于y轴对称,则m、n的值为( )
A.m=1,n=﹣1 B.,
C.m=﹣5,n=7 D.,
【分析】让两点的纵坐标相等,横坐标互为相反数列式求值即可.
【解答】解:∵点A(2m,2﹣m)和点B(3+n,n)关于y轴对称,
∴2m+3+n=0,2﹣m=n,
解得:m=﹣5,n=7,
故选:C.
8.(3分)如图,若圆柱的底面周长是14cm,高是48cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.49cm B.50cm C.54cm D.64cm
【分析】将圆柱侧面展开可得到长为48cm,宽为圆柱的底面周长14cm的矩形,根据勾股定理即可求出AB的长,即为所求.
【解答】解:如图,圆柱侧面展开图是矩形,
矩形的长为48cm,宽为圆柱的底面周长14cm,
根据勾股定理得:
AB==50(cm),
根据两点之间线段最短,可得丝线的最小长度为50cm,
故选:B.
9.(3分)一次函数y=kx+b与y=kbx,它们在同一坐标系内的图象可能为( )
A. B.
C. D.
【分析】根据一次函数的图象与系数的关系,有由一次函数y=kx+b图象分析可得k、b的符号,进而可得k•b的符号,从而判断y=kbx的图象是否正确,进而比较可得答案.
【解答】解:根据一次函数的图象分析可得:
A、由一次函数y=kx+b图象可知k<0,b>0;一次函数y=kbx的图象可知kb<0,两函数解析式均成立;
B、由一次函数y=kx+b图象可知k<0,b>0;即kb<0,与次函数y=kbx的图象可知kb>0矛盾;
C、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与次函数y=kbx的图象可知kb>0矛盾;
D、由一次函数y=kx+b图象可知k>0,b>0;即kb>0,与次函数y=kbx的图象可知kb<0矛盾.
故选:A.
10.(3分)如图,平行于x轴的直线l与y轴、直线y=3x、直线y=x分别交于点A、B、C.则下列结论正确的个数有( )
①∠AOB+∠BOC=45°;②BC=2AB;③OB2=10AB2;④OC2=OB2.
A.1个 B.2个 C.3个 D.4个
【分析】由直线y=x得出∠AOC=45°,得出①正确;
由直线y=3x和y=x得出OA=3AB,OA=AC,因此AC=3AB,BC=2AB,得出②正确;
由勾股定理得出③正确,④不正确;即可得出结论.
【解答】解:∵直线y=x,
∴∠AOC=45°,
即∠AOB+∠BOC=45°,
∴①正确;
∵平行于x轴的直线l与直线y=3x、直线y=x分别交于点B、C,
∴OA=3AB,OA=AC,
∴AC=3AB,
∴BC=2AB,
∴②正确;
∵OB2=AB2+OA2=AB2+(3AB)2=10AB2,
∴③正确;
∵OC2=OA2+AC2=(3AB)2+(3AB2)=18AB2=OB2=OB2,
∴④不正确;
结论正确的有3个,
故选:C.
二、填空题(每小题3分,共15分)
11.(3分)若的值在两个整数a与a+1之间,则a= 3 .
【分析】利用的取值范围,进而得出的取值范围进而得出答案.
【解答】解:∵的值在两个整数a与a+1之间,,
∴a=3.
故答案为:3.
12.(3分)若y=(k﹣2)+2是一次函数,则k= ﹣2
【分析】根据一次函数的定义列出方程k2﹣3=1,且k﹣2≠0,由此求得k的值.
【解答】解:依题意得:k2﹣3=1,且k﹣2≠0,
解得k=﹣2.
故答案是:﹣2.
13.(3分)如图,长方形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是﹣1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则这个点E表示的实数是 ﹣1 .
【分析】首先根据勾股定理计算出AC的长,进而得到AE的长,再根据A点表示﹣1,可得点E表示的实数.
【解答】解:∵AD长为2,AB长为1,
∴AC==,
∵A点表示﹣1,
∴点E表示的实数是﹣1.
故答案为:﹣1.
14.(3分)对于任意的正数m、n定义运算※为:m※n=,计算(3※2)×(8※12)的结果为 2 .
【分析】根据新定义把所求的式子化为二次根式的和、积的形式,根据二次根式的混合运算法则计算即可.
【解答】解:(3※2)×(8※12)
=(﹣)×(+)
=(﹣)×2(+)
=2,
故答案为:2.
15.(3分)如图,一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为 (﹣6,0)或(,0) .
【分析】根据勾股定理得到AB=5,如图1,当点A落在y轴的正半轴上时,如图2,当点A落在y轴的负半轴上时,根据勾股定理即可得到结论.
【解答】解:∵一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=5,
如图1,当点A落在y轴的正半轴上时,
设点C的坐标为(m,0),
∵将△ABC沿BC所在的直线折叠,当点A落在y轴上时,
∴A′O=3+5=8,A′C=AC=4﹣m,
∵A′C2=OC2+A′O2,
∴(4﹣m)2=m2+82,
∴m=﹣6;
如图2,当点A落在y轴的负半轴上时,
设点C的坐标为(m,0),
∵将△ABC沿BC所在的直线折叠,当点A落在y轴上时,
∴A′O=5﹣3=2,A′C=AC=4﹣m,
∵A′C2=OC2+A′O2,
∴(4﹣m)2=m2+22,
∴m=;
综上所述,当点A落在y轴上时,点C的坐标为(﹣6,0)或(,0),
故答案为:(﹣6,0)或(,0).
三、解答题(第16题6分、第17题6分、第18题8分、第19题8分、第20题8分、第21题10分、第22题10分,共55分)
16.(6分)计算:(1);
(2).
【分析】根据二次根式混合运算的法则计算即可.
【解答】解:(1)原式=2﹣﹣+=;
(2)原式=7﹣5+3﹣4+8=13﹣4.
17.(6分)(1)已知:2a+1的算术平方根是3,3a﹣b﹣1的立方根是2,求的值.
(2)已知10+=x+y,其中x是整数,且0<y<1,求x﹣y+的算术平方根.
【分析】(1)根据算术平方根和立方根的定义求出a,b的值,代入求值即可;
(2)估算出10+的范围,得到x,y的值,求出x﹣y+的值,再求算术平方根即可.
【解答】解:(1)∵2a+1的算术平方根是3,3a﹣b﹣1的立方根是2,
∴2a+1=32=9,3a﹣b﹣1=23=8,
∴a=4,b=3,
∴===4;
(2)∵1<3<4,
∴1<<2,
∴11<10+<12,
∵x是整数,且0<y<1,
∴x=11,y=10+﹣11=﹣1,
∴x﹣y+=11﹣+1+=12,
∴12的算术平方根是=2,
∴x﹣y+的算术平方根为2.
18.(8分)如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在图中画出△ABC,△ABC的面积是 4 ;
(2)若点D与点C关于y轴对称,则点D的坐标为 (﹣4,3) ;
(3)已知Q为y轴上一点,若△ACQ的面积为8,求点Q的坐标.
【分析】(1)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(2)利用关于y轴对称点的性质得出答案;
(3)利用三角形面积求法得出符合题意的答案.
【解答】解:(1)如图所示:△ABC的面积是:3×4﹣×1×2﹣×2×4﹣×2×3=4;
故答案为:4;
(2)点D与点C关于y轴对称,则点D的坐标为:(﹣4,3);
故答案为:(﹣4,3);
(3)∵Q为y轴上一点,△ACQ的面积为8,
∴AQ•4=8
AQ=4,
故Q点坐标为:(0,5)或(0,﹣3).
19.(8分)为了鼓励居民节约用水,某市采用“阶梯水价”的方法按月计算每户家庭的水费:每月用水量不超过20吨时,按每吨2元计费;每月用水量超过20吨时,其中的20吨仍按每吨2元计费,超过部分按每吨2.8元计费,设每户家庭每月用水量为x吨时,应交水费y元.
(1)分别求出0≤x≤20和x>20时,y与x之间的函数表达式;
(2)小颖家四月份、五月份分别交水费45.6元、38元,问小颖家五月份比四月份节约用水多少吨?
【分析】(1)因为月用水量不超过20吨时,按2元/吨计费,所以当0≤x≤20时,y与x的函数表达式是y=2x;因为月用水量超过20吨时,其中的20吨仍按2元/吨收费,超过部分按2.8元/吨计费,所以当x>20时,y与x的函数表达式是y=2×20+2.8(x﹣20),即y=2.8x﹣16;
(2)由题意可得:因为五月份缴费金额不超过40元,所以用y=2x计算用水量;四月份缴费金额超过40元,所以用y=2.8x﹣16计算用水量,进一步得出结果即可.
【解答】解:(1)当0≤x≤20时,y与x的函数表达式是y=2x;
当x>20时,y与x的函数表达式是y=2×20+2.8(x﹣20)=2.8x﹣16;
(2)因为小颖家五月份的水费都不超过40元,四月份的水费超过40元,
所以把y=38代入y=2x中,得x=19;
把y=45.6代入y=2.8x﹣16中,得x=22.
所以22﹣19=3吨.
答:小颖家五月份比四月份节约用水3吨.
20.(8分)如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,将△ABE沿AE折叠,使点B落在B'处.
(1)若∠CEB'=70°,求∠DAB'.
(2)若点B'恰好在矩形ABCD的对角线AC上,求BE的长.
【分析】(1)由矩形的性质得∠BAD=∠B=90°,再由折叠的性质得∠BEA=∠B′EA,∠BAE=∠B′AE,则∠BEA=∠B′EA=55°,得∠BAE=35°,则∠BAB′=70°,即可求解;
(2)由折叠的性质得BE=B′E,AB=AB′=6,∠B=∠AB′E=90°,设BE=B′E=x,则CE=BC﹣BE=8﹣x,再在Rt△CB′E中,由勾股定理得出方程,解方程即可.
【解答】解:(1)∵四边形ABCD是矩形,
∴∠BAD=∠B=90°,
由折叠的性质得:∠BEA=∠B′EA,∠BAE=∠B′AE,
∵∠CEB′=70°,
∴∠BEB′=180°﹣70°=110°,
∴∠BEA=∠B′EA=×110°=55°,
∴∠BAE=90°﹣55°=35°,
∴∠BAB′=2×35°=70°,
∴∠DAB′=∠BAD﹣∠BAB′=90°﹣70°=20°;
(2)点B'恰好在矩形ABCD的对角线AC上,如图:
在Rt△ABC中,由勾股定理得:AC===10,
由折叠的性质得:BE=B′E,AB=AB′=6,∠B=∠AB′E=90°,
∴B′C=AC﹣AB′=10﹣6=4,∠CB′E=90°,
设BE=B′E=x,
则CE=BC﹣BE=8﹣x,
在Rt△CB′E中,由勾股定理得:CE2=B′E2+B′C2,
即:(8﹣x)2=x2+42,
解得:x=3,
∴BE的长为3.
21.(10分)“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a= 10 ,b= 15 ,m= 200 ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发后至到达图书馆前,何时与小军相距100米,请求出此时小军骑行的时间.(直接写出答案)
【分析】(1)由时间=求a,a+5=b,再由B到C段的速度=求m.
(2)分别求出小军运动y与x的关系式及BC段直线解析式,联立方程求解.
(3)由120x﹣(200x﹣1500)=100或200x﹣1500﹣120x=100求解.
【解答】解:(1)由题意得a=1500÷150=10,
b=10+5=15,
m=(3000﹣1500)÷(22.5﹣15)=200(米/分),
故答案为:10,15,200.
(2)设BC所在直线解析式为y=kx+b,
将(15,1500),(22.5,3000)代入y=kx+b得:
,
解得,
∴y=200x﹣1500(15≤x≤22.5),
∵小军速度为120米/分,
∴OD所在直线解析式为y=120x,
联立方程,
解得,
3000﹣2250=750(米),
∴小军在途中与爸爸第二次相遇时,距离图书馆750米.
(3)由题意得当x<时,120x﹣(200x﹣1500)=100,
解得x==17.5,
当x>时,200x﹣1500﹣120x=100,
解得x=20.
∴爸爸自第二次出发至到达图书馆前,小军骑行时间为17.5或20分钟时,两人相距100米.
22.(10分)如图,在平面直角坐标系中,直线y=﹣2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
(1)求点C的坐标.
(2)若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.
(3)在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.
【分析】(1)联立两直线解析式成方程组,得:,即可求解;
(2)分PC=PO、PC=OC、PO=OC分别求解即可;
(3)S△OAC=×6×4=12.设M(x,y)当M在x轴下方时△MOC的面积是△AOC面积的2倍,△MOA的面积等于△AOC的面积,|y|=4;当M在x轴上方时△MOC的面积是△AOC面积的2倍,△MOA的面积等于△AOC的面积的3倍,|y|=12;即可求解.
【解答】解:(1)联立两直线解析式成方程组,得:,
解得:,
∴点C的坐标为(4,4);
(2)设点P(m,0),而点C(4,4),点O(0,0);
PC2=(m﹣4)2+16,PO2=m2,OC2=32;
当PC=PO时,(m﹣4)2+16=m2,解得:m=4;
当PC=OC时,同理可得:m=0(舍去)或8;
当PO=OC时,同理可得:m=;
故点P的坐标为:(4,0)或(8,0)或(,0)或(,0);
(3)当y=0时,有0=﹣2x+12,
解得:x=6,
∴点A的坐标为(6,0),
∴OA=6,
∴S△OAC=×6×4=12.
设M(x,y)当M在x轴下方时,△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积,|y|=4
当y=﹣4时,﹣4=﹣2x+12,x=8,
∴M(8,﹣4),
当M在x轴上方时,△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积的3倍,|y|=12;
当y=12时,12=﹣2x+12,x=0,
∴M(0,12),
综上所述,M(8,﹣4)或(0,12).
广东省深圳市龙岗区龙岭初级中学八年级(上)月考数学试卷: 这是一份广东省深圳市龙岗区龙岭初级中学八年级(上)月考数学试卷,共19页。
精品解析:广东省深圳市龙岗区宏扬学校2021-2022学年八年级上学期期中数学试卷: 这是一份精品解析:广东省深圳市龙岗区宏扬学校2021-2022学年八年级上学期期中数学试卷,文件包含精品解析广东省深圳市龙岗区宏扬学校2021-2022学年八年级上学期期中数学试卷原卷版docx、精品解析广东省深圳市龙岗区宏扬学校2021-2022学年八年级上学期期中数学试卷解析版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。
2022-2023学年广东省深圳市龙岗区联邦学校等两校八年级(上)期中数学试卷(解析版): 这是一份2022-2023学年广东省深圳市龙岗区联邦学校等两校八年级(上)期中数学试卷(解析版),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












