



高中数学上教版(2020)必修 第二册7.1 正弦函数的图像与性质优秀备课ppt课件
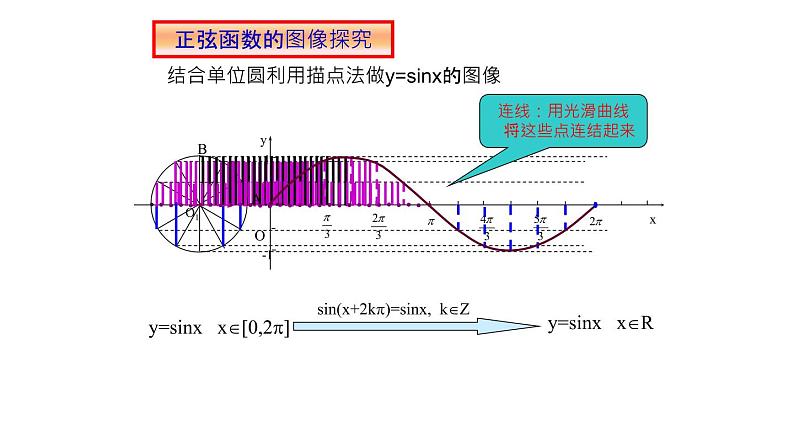
展开结合单位圆利用描点法做y=sinx的图像
y=sinx x[0,2]
y=sinx xR
sin(x+2k)=sinx, kZ
连线:用光滑曲线 将这些点连结起来
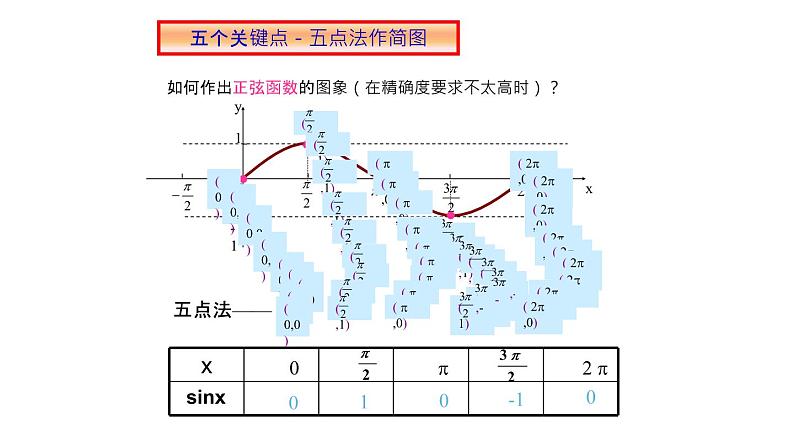
1.正弦函数的图像(1)“五点法”画图:在精确度要求不太高时,我们可以找出正弦曲线上的(0,0),________, _______,__________,(2π,0)五个关键点画出正弦函数在一个周期上的图像.
(2)正弦曲线:将函数y=sin x(x∈[0,2π])的图像向左、向右平行移动(每次平移____个单位长度),就可以得到正弦函数y=sin x(x∈R)的图像._________的图像叫作正弦曲线.
【思考】利用五点法作函数y=Asin x(A>0)的图像时,选取的五个关键点是什么?提示:依次是(0,0), ,(π,0), ,(2π,0).
如何作出正弦函数的图象(在精确度要求不太高时)?
五个关键点-五点法作简图
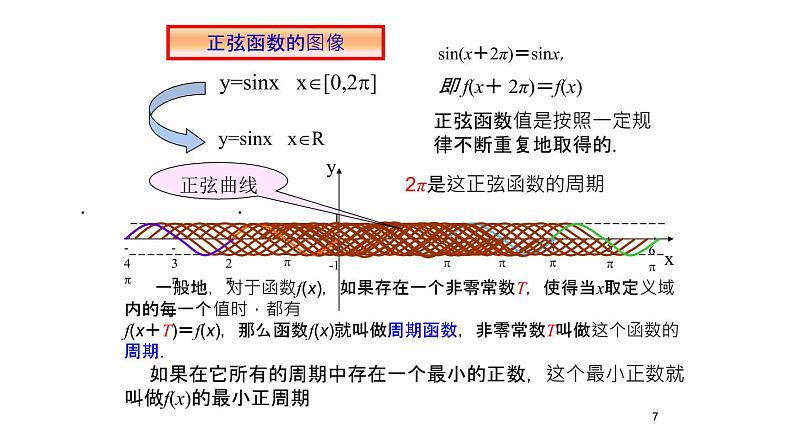
sin(x+2π)=sinx,
即 f(x+ 2π)=f(x)
正弦函数值是按照一定规律不断重复地取得的.
2π是这正弦函数的周期
一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.
如果在它所有的周期中存在一个最小的正数,这个最小正数就叫做f(x)的最小正周期
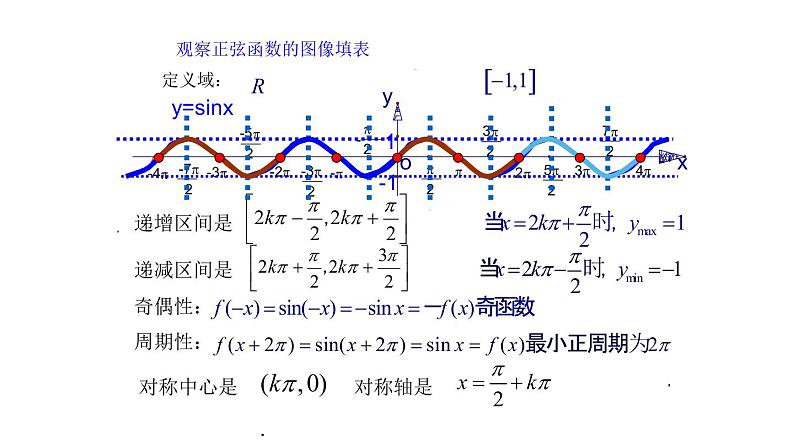
观察正弦函数的图像填表
【思考】如何求正弦函数的递增区间?提示:求一个完整的递增区间,例如, ,再在区间两个端点上加周期的整数倍,即 ,k∈Z.
【基础小测】1.辨析记忆(对的打“√”,错的打“×”)(1)用“五点法”画图时的“五点”是正弦函数图像的一个最高点,一个最低点,三个和x轴的交点.( )(2)函数y=sin x的图像关于原点对称.( )(3)正弦函数y=sin x是周期函数.( )(4)正弦函数y=sin x的最大值为1,最小值为-1.( )
提示:(1)√.由“五点法”作图的五点坐标可知(1)是正确的.(2)√.函数y=sin x为奇函数,其图像关于原点对称.(3)√.正弦函数y=sin x是周期为2π的周期函数.(4)√.根据正弦函数的性质可知.
2.点M 在函数y=sin x的图像上,则m的值为( )【解析】选B.将 代入y=sin x中,得m=
求下列三角函数的周期:
因为sin(2+z)=sinz
即 f (x+2)=f (x)
则3sin(z+2)=3sinz
即 f (x+4)=f (x)
∴周期T=4
(1)y=sin2x(x∈R)的周期为2π/2=π;
的周期为2π/(1/2)=4π.
函数 在什么区间上是增函数?
∴ 函数 在区间
类型一 “五点法”作函数的图像(直观想象)【题组训练】 1.利用“五点法”作出y=-2+sin x(x∈[0,2π])的简图.2.作出函数y=-2sin x(0≤x≤2π)的简图.
【解析】1.按五个关键点列表:
描点并将它们用光滑的曲线连接起来(如图所示)
2.按五个关键点列表:
描点并将它们用光滑的曲线连接起来(如图所示).
【解题策略】“五点法”作图中“五点”的含义
【拓展延伸】正弦曲线的简单变换(1)函数y=-sin x的图像与y=sin x的图像关于x轴对称.(2)函数y=sin x与y=sin x+k的图像间的关系.当k>0时,把y=sin x的图像向上平移k个单位得到函数y=sin x+k的图像;当k<0时,把y=sin x的图像向下平移|k|个单位得到函数y=sin x+k的图像.
【补偿训练】(1)用“五点法”画出函数y=2sin x(0≤x≤2π)的图像.(2)用“五点法”画出函数y=sin 2x(0≤x≤π)的图像.
【解析】 (1)列表:
描点得y=sin 2x(0≤x≤π)的简图,如图:
类型二 正弦函数图像的应用(直观想象) 角度1 解不等式 【典例】利用y=sin x的图像,在[0,2π]内求满足sin x≥- 的x的范围.【思路导引】画出y=sin x在[0,2π]内的图像,数形结合可解.
描点,连线如图,同时作出直线y=- 的图像.
由图像可得sin x≥- 的范围是 .
角度2 判断方程解的个数 【典例】方程|sin x|= 的根中,在[0,2]内的有( ) A.1个B.2个C.3个D.4个【思路导引】分别画出y=|sin x|与y= 的图像,求出它们在[0,2]内的交点,交点的横坐标即为|sin x|= 的根.
【解析】选A.画出y=|sin x|与y= 的图像,如图所示,在区间[0,π]内它们的交点为 , ,即|sin x|= 的两个根为 和 ,
又因为2< ,所以在区间[0,2]内|sin x|= 只有一个根 .
【变式探究】求方程lg x=sin x的实数解的个数.【解析】作出y=lg x,y=sin x在同一坐标系内的图像,则方程根的个数即为两函数图像交点的个数,由图像知方程有三个实根.
角度3 求参数的取值范围 【典例】函数f(x)=sin x+2|sin x|,x∈[0,2π]的图像与直线y=k有且仅有两个不同的交点,求实数k的取值范围.【思路导引】画出函数f(x)的图像,通过平移y=k求解k的取值范围.
【解析】y=f(x)= 作出图像,如图
因为f(x)图像与直线y=k有且仅有两个不同交点.所以1
【题组训练】 利用正弦曲线,求满足
【解析】1.(1)因为sin =-sin ,sin =-sin =-sin ,由于 且y=sin x在 上是减少的,所以sin >sin ,所以-sin <-sin ,即sin
2.y=2sin =-2sin ,令z=x- ,则y=-2sin z.因为z是x的一次函数,所以要求y=-2sin z的递增区间,即求sin z的递减区间,即2kπ+ ≤z≤2kπ+ (k∈Z).所以2kπ+ ≤x- ≤2kπ+ (k∈Z),
即2kπ+ ≤x≤2kπ+ (k∈Z),所以函数y=2sin 的递增区间为 (k∈Z).
【解题策略】1.利用函数的单调性比较大小的步骤(1)先将异名化同名,即统一为正弦函数.(2)将不是同一单调区间的角用诱导公式转化到同一单调区间.(3)利用单调性来比较大小.2.求三角函数单调区间的方法确定正弦函数单调区间的基本思想是整体换元思想.若x的系数为负,通常利用诱导公式化为正数再求解.有时还应兼顾函数的定义域.
【补偿训练】1.在下列各区间中,函数y=sin 的递增区间是( )A. B. C.[-π,0]D. 【解析】选B.由- +2kπ≤x+ ≤ +2kπ,k∈Z,得- +2kπ≤x≤ +2kπ,显然,当x∈ 时,函数是增加的.
2.比较sin 194°与cs 110°的大小.【解析】因为sin 194°=sin(180°+14°)=-sin 14°,cs 110°=cs(180°-70°)=-cs 70°=-sin(90°-70°)=-sin 20°,由于0°<14°<20°<90°,而y=sin x在 上是增加的,所以sin 14°
类型四 正弦函数的最值(值域)问题(数学运算)【典例】1.y=-2sin x,x∈ 的最大值为________,最小值为________. 2.求下列函数的值域.(1)y=3-2sin x.(2)y=-sin2x+ sin x+ .【思路导引】1.利用正弦函数的单调性求解.2.(1)利用正弦函数的范围,逐步求解.(2)转化为二次函数求最值问题.
【解析】1.y=sin x在 上是增加的,在 上是减少的,y=-2sin x在 上是减少的,在 上是增加的,当x=- 时,ymax=1;当x= 时,ymin=-2.答案:1 -2
2.(1)因为-1≤sin x≤1,所以-1≤-sin x≤1,1≤3-2sin x≤5,所以函数y=3-2sin x的值域为[1,5].(2)令t=sin x,则-1≤t≤1,y=-t2+ t+ =- +2,所以当t= 时,ymax=2.此时sin x= ,
即x=2kπ+ 或x=2kπ+ ,k∈Z.当t=-1时,ymin= .此时sin x=-1,即x=2kπ+ ,k∈Z.所以函数y=-sin2x+ sin x+ 的值域为 .
【解题策略】1.正弦函数在定区间上的值域求正弦函数在定区间上的值域时,首先要考查正弦函数在该区间上是否单调,若是单调函数,则直接代入端点值即可;若不是单调函数,则要结合图像,确定正弦函数在该区间上的最高点、最低点后再求最值.2.求正弦型函数最值的常用方法(1)形如y=asin x的函数的最值要注意对a的讨论.(2)形如y=asin2x+bsin x+c的函数可以通过换元,把函数化为二次函数求值域.提醒:换元后忽视新元范围的确定是易错点.
【跟踪训练】1.若sin x=2m+3,且x∈ ,则m的取值范围为( ) 【解析】选C.因为x∈ ,所以结合图像知sin x∈ ,即- ≤2m+3≤ .所以 即m的取值范围为 .
2.求f(x)=2sin2x+2sin x- ,x∈ 的值域.【解析】令t=sin x,则g(t)=2t2+2t- .因为x∈ ,所以 ≤sin x≤1,即 ≤t≤1,所以g(t)=2 -1,t∈ 且该函数在 上是增加的.所以f(x)min=g =1,f(x)max=g(1)= .所以f(x)=2sin2x+2sin x- ,x∈ 的值域为 .
备选类型 正弦函数的周期性与奇偶性(逻辑推理)【典例】1.求下列函数的周期:(1)y=sin x.(2)y=|sin x|.2.判断下列函数的奇偶性:(1)f(x)=xsin x.(2)f(x)=|sin x|+1.
【解析】1.(1)因为sin =sin =sin x,所以y=sin x的周期是4π.(2)作出y=|sin x|的图像,如图.
故周期为π.2.(1)因为x∈R,且关于原点对称,又f(-x)=-xsin(-x)=xsin x=f(x),所以f(x)为偶函数.(2)因为x∈R,且关于原点对称,又f(-x)=|sin(-x)|+1=f(x),所以f(x)为偶函数.
【解题策略】1.求正弦函数的周期时要注意结合图像判断,不要盲目套用结论.2.函数y=sin x为奇函数时其定义域必须关于原点对称,否则不具有奇偶性.如y=sin x,x∈[0,2π]是非奇非偶函数.
【跟踪训练】1.函数f(x)= sin 2x的奇偶性为( )A.奇函数 B.偶函数C.既是奇函数又是偶函数 D.非奇非偶函数
【解析】选A.f(x)= sin 2x,f(-x)= sin(-2x)=- sin 2x,所以f(-x)=-f(x),且定义域为R,所以f(x)= sin 2x为奇函数.
2.函数f(x)=3+sin x的最小正周期是( )A. B.πC. D.2π【解析】选D.由3+sin(2π+x)=3+sin x知f(x)的最小正周期为2π.
3.下列函数中是奇函数的是( ) A.y=-|sin x|B.y=sin(-|x|)C.y=sin|x|D.y=xsin|x|【解析】选D.利用奇偶性定义,显然y=f(x)=xsin|x|满足f(-x)=-f(x),是奇函数.
4.若0
令x=0,有2x=3sin x;令x= ,有2x<3sin x;令x= ,有2x>3sin x.
5.求函数y=3-2sin 的最值及取到最值时的自变量x的集合.【解析】因为-1≤sin x≤1,所以当sin x=-1, x=2kπ- ,k∈Z,即x=4kπ-π,k∈Z时,ymax=5,此时自变量x的集合为{x|x=4kπ-π,k∈Z};当sin x=1, x=2kπ+ ,k∈Z,即x=4kπ+π,k∈Z时,ymin=1,此时自变量x的集合为{x|x=4kπ+π,k∈Z}.
高中数学北师大版 (2019)必修 第二册5.1 正弦函数的图象与性质再认识备课课件ppt: 这是一份高中数学北师大版 (2019)必修 第二册5.1 正弦函数的图象与性质再认识备课课件ppt,共22页。PPT课件主要包含了新知初探,奇函数,补充对称性,基础检测,正弦函数的图像,正弦函数的性质,布置作业,y=sinx的性质等内容,欢迎下载使用。
上教版(2020)必修 第二册6.2 常用三角公式备课课件ppt: 这是一份上教版(2020)必修 第二册6.2 常用三角公式备课课件ppt,共21页。PPT课件主要包含了温故知新,C-等内容,欢迎下载使用。
上教版(2020)必修 第二册6.1 正弦、余弦、正切、余切备课课件ppt: 这是一份上教版(2020)必修 第二册6.1 正弦、余弦、正切、余切备课课件ppt,共26页。PPT课件主要包含了任意角三角函数的定义,1正弦sinα=,2余弦cosα=,3正切tanα=,三角函数的符号,公式一,由三角函数的定义得,P-x-y,公式二,诱导公式的推导等内容,欢迎下载使用。













