数学九年级上册24.1.2 垂直于弦的直径课文课件ppt

这是一份数学九年级上册24.1.2 垂直于弦的直径课文课件ppt，共20页。PPT课件主要包含了圆的对称性，赵州桥，作垂线段连半径，活动4，≤OM≤5，或17等内容，欢迎下载使用。

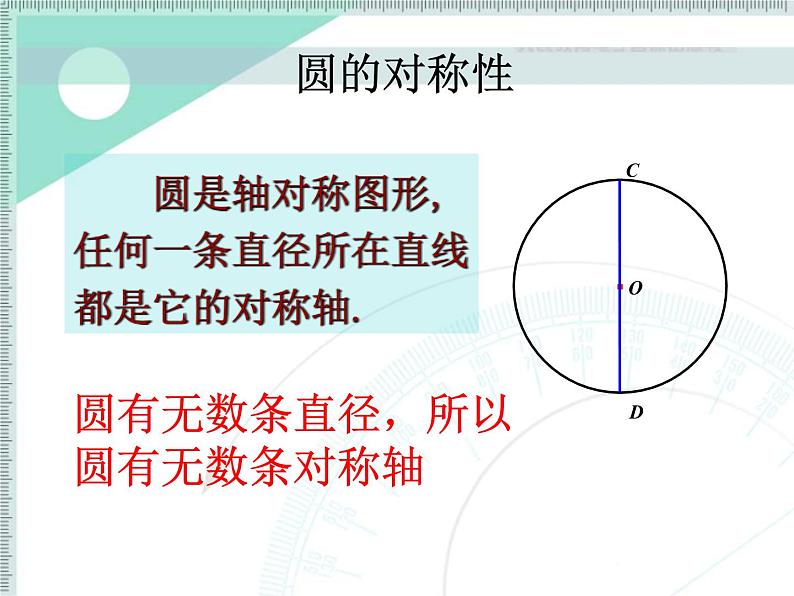
圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
圆有无数条直径，所以圆有无数条对称轴
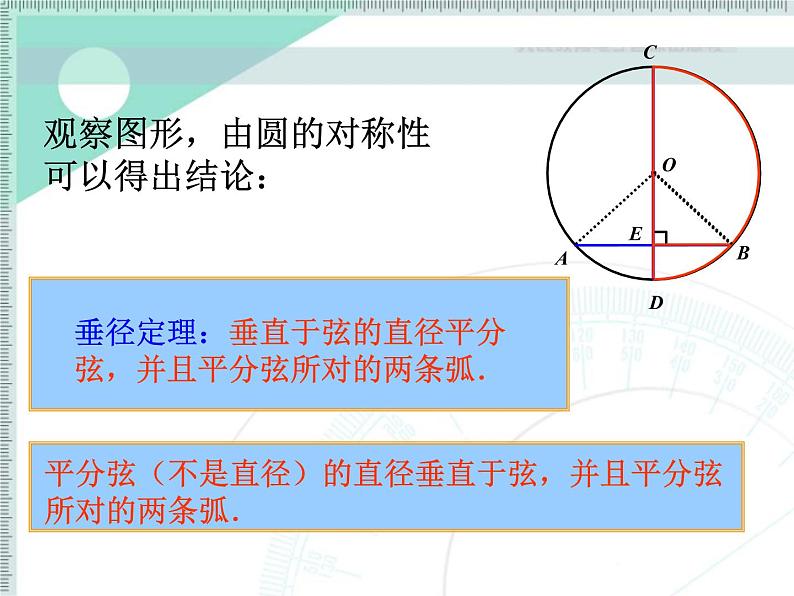
平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
观察图形，由圆的对称性可以得出结论：
“知二推三” (1)垂直于弦 (2)过圆心 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧注意:当具备了(1)(3)时,应对弦增加”不是直径”的限制.
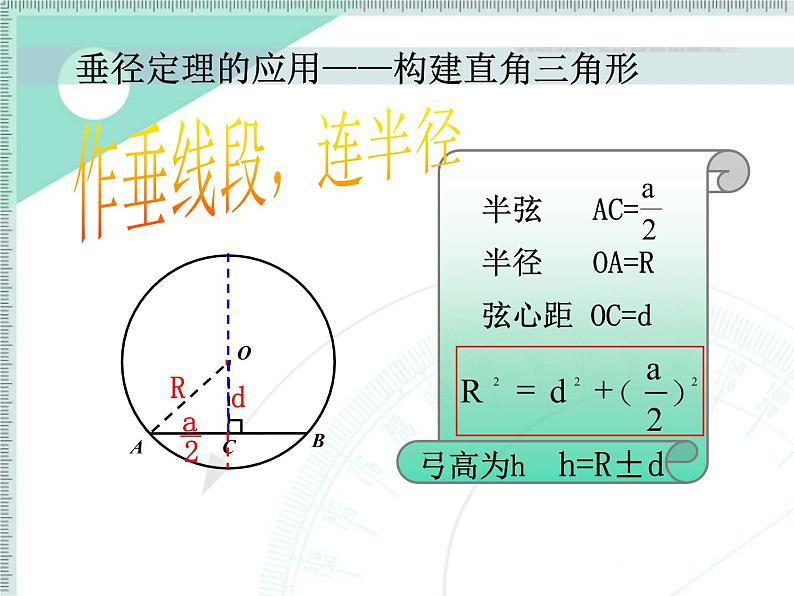
例题1：如图在⊙O中，弦AB的长为 8cm，圆心O到AB的距离为3cm，求圆0的半径。
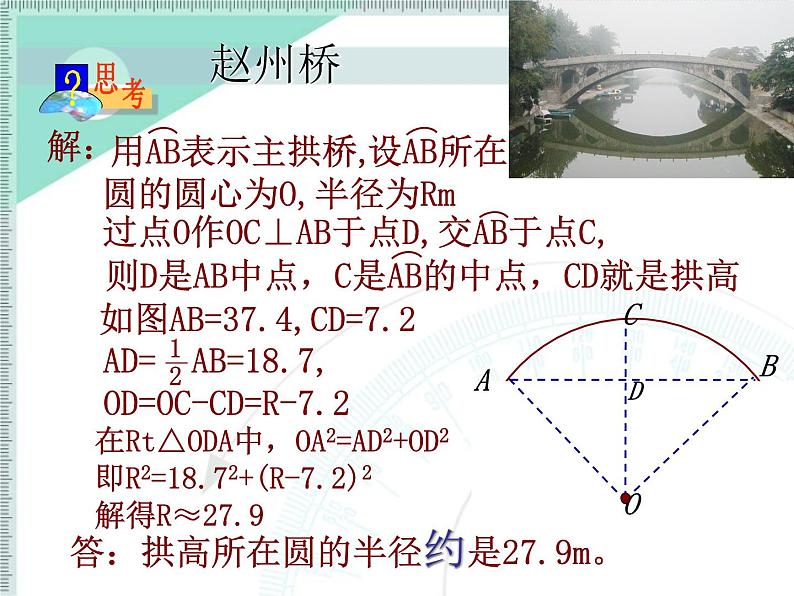
在Rt△ODA中，OA2=AD2+OD2即R2=18.72+(R-7.2)2解得R≈27.9
如图AB=37.4,CD=7.2
答：拱高所在圆的半径约是27.9m。
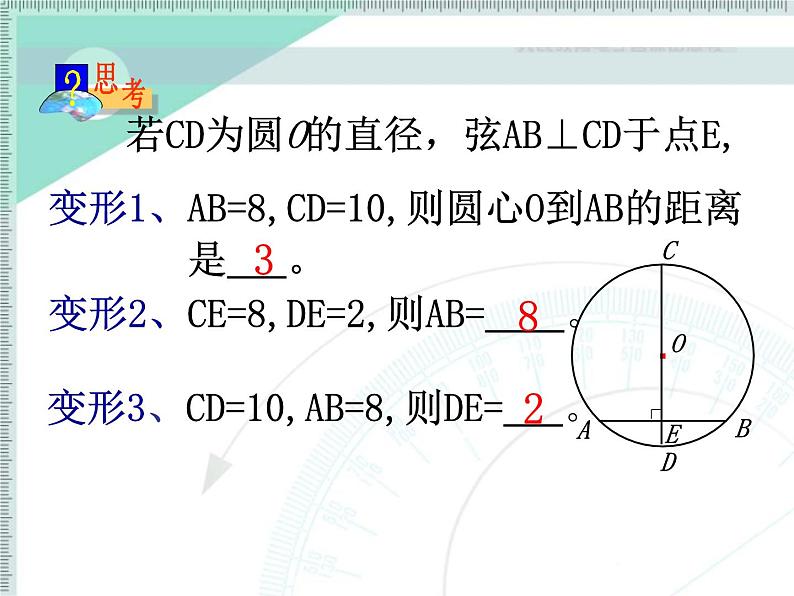
变形2、CE=8,DE=2,则AB= 。
变形1、AB=8,CD=10,则圆心O到AB的距离 是 。
变形3、CD=10,AB=8,则DE= 。
若CD为圆O的直径，弦AB⊥CD于点E,
垂径定理的应用——构建直角三角形
如图，两个圆都以点O为圆心，求证:AC=BD．
在△ABC中，∠C=900，AC=6，BC=8，以C为圆心，AC为半径的圆交斜边AB于D，求AD的长。
变形4、若⊙O的直径为10，弦AB=8，E是AB上任意一动点,则OE的最小值是 。
变形5、线段OE长的取值范围的是 。
2．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．
∴四边形ADOE为矩形，
∴ 四边形ADOE为正方形.
∵ OE⊥AC OD⊥AB
变形5、半径为5的⊙O内有一点P,且OP=3,则过点P的最短的弦长是 ，最长的弦长是 。
6．如图所示，破残的圆形轮片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D。已知：AB=24cm，CD=8cm （1）求作此残片所在的圆（不写作法，保留作图痕迹）； （2）求（1）中所作圆的半径.
7．如图， ⊙O的直径AB垂直弦CD于P，且是半径OB的中点，CD=6cm，则直径的长是（　） A． B． C． D．
8．已知AB是⊙O的直径，弦CD⊥AB，E为垂足，CD=8，OE=1，则AB=____________9．如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C， 且CD＝l，则弦AB的长是 _______
10．某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示，已知AB＝16m，半径OA＝10m，则中间柱CD的高度为 m
11．如图，在直角坐标系中，以点P为圆心的圆弧与轴交于A、B两点，已知P(4，2)和A(2，0)，则点B的坐标是_______
12．如图，⊙O的半径是5cm，P是⊙O外一点,PO=8cm，∠P=30º,则AB= cm
13．⊙O的半径为13 cm，弦AB∥CD，AB＝24cm，CD＝10cm，那么AB和CD的距离是 _________Cm
14．已知AB是圆O的弦，半径OC垂直AB，交AB于D，若AB=8，CD=2，则圆的半径为_______
15．如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心，则折痕的长为____