






人教版九年级上册24.1.2 垂直于弦的直径教学ppt课件
展开【问题1】把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
任何一条直径所在直线或经过圆心的直线都是圆的对称轴.
【问题2】圆有几条对称轴?
考点 1:垂径定理的推论1
考点2:垂径定理的推论2
考点3:垂径定理的推论3
考点4:垂径定理的推论4
【探究1】垂径定理的条件和结论分别是什么?
条件:①过圆心, ②垂直于弦.
结论:③平分弦, ④平分弦所对的劣弧, ⑤平分弦所对的优弧.
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
【探究2】如果把垂径定理结论与题设交换一条,命题是真命题吗? ①过圆心; ②垂直于弦; ③平分弦; ④平分弦所对的优弧; ⑤平分弦所对的劣弧.
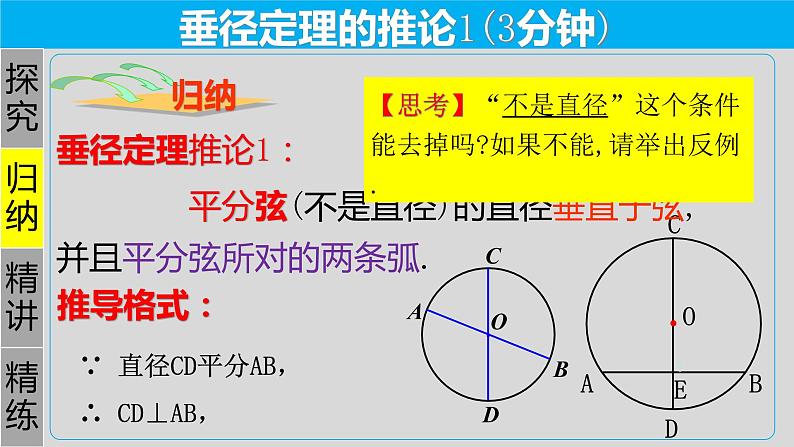
垂径定理的推论1(3分钟)
2.交换②,③得到一个新命题,这个命题是真命题吗?
条件:①过圆心, ③平分弦.
结论:②垂直于弦, ④平分弦所对的劣弧, ⑤平分弦所对的优弧.
证明:(1)连接AO,BO,则AO=BO, ∵AE=BE,∴△AOE≌△BOE(SSS), ∴∠AEO=∠BEO=90º,∴CD⊥AB. (2)由垂径定理可得AC=BC,AD=BD.
用语言叙述这个结论吗?
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
∵ 直径CD平分AB,
【思考】“不是直径”这个条件能去掉吗?如果不能,请举出反例.
垂径定理的推论2(3分钟)
3.若交换①,③一个新命题,它也是真命题吗?
条件:②垂直于弦, ③平分弦.
结论:①过圆心, ④平分弦所对的劣弧, ⑤平分弦所对的优弧.
你能用语言叙述这个结论吗?
弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
∵ AE=BE,CD⊥AB,
【例2】怎样将一个如图所示的破损的圆盘复原了吗?
方法:1.在圆弧上任取三点A、B、C;2.作线段AB、BC的垂直平分线,其交点O即为圆心;3.以点O为圆心,OC长为半径作圆.⊙O即为所求.
垂径定理的推论3(3分钟)
4.再交换一个条件和结论得到一个新命题,它也是真命题吗?
条件:②垂直于弦; ④平分弦所对的劣弧.
结论:①过圆心; ③平分弦; ⑤平分弦所对的优弧.
平分弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧.
小结:如果一条直线具有:①过圆心;②垂直于弦;③平分弦;④平分弦所对的劣弧;⑤平分弦所对的优弧;这五个条件中的两个,就可以推出另外三个性质,简称“知二推三”
垂径定理的推论4(3分钟)
证明:作直径MN⊥AB. ∵AB∥CD,∴MN⊥CD.则AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弧) AM-CM=BM-DM ∴AC=BD
夹在两平行弦之间的弧相等。
解决有关弦的问题,经常是过圆心作弦的弦心距,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.
初中数学人教版九年级上册24.1.2 垂直于弦的直径教学课件ppt: 这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径教学课件ppt,共24页。PPT课件主要包含了做一做等内容,欢迎下载使用。
人教版九年级上册24.1.2 垂直于弦的直径示范课ppt课件: 这是一份人教版九年级上册24.1.2 垂直于弦的直径示范课ppt课件,共27页。PPT课件主要包含了教学目标,复习回顾,新知探究,归纳小结,巩固练习,课堂练习,课堂总结等内容,欢迎下载使用。
初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径课文配套ppt课件: 这是一份初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径课文配套ppt课件,共36页。PPT课件主要包含了复习回顾等内容,欢迎下载使用。













