2020-2021学年北京市朝阳区七年级（上）期末数学试卷（选用）

2020-2021学年北京市朝阳区七年级（上）期末数学试卷（选用）

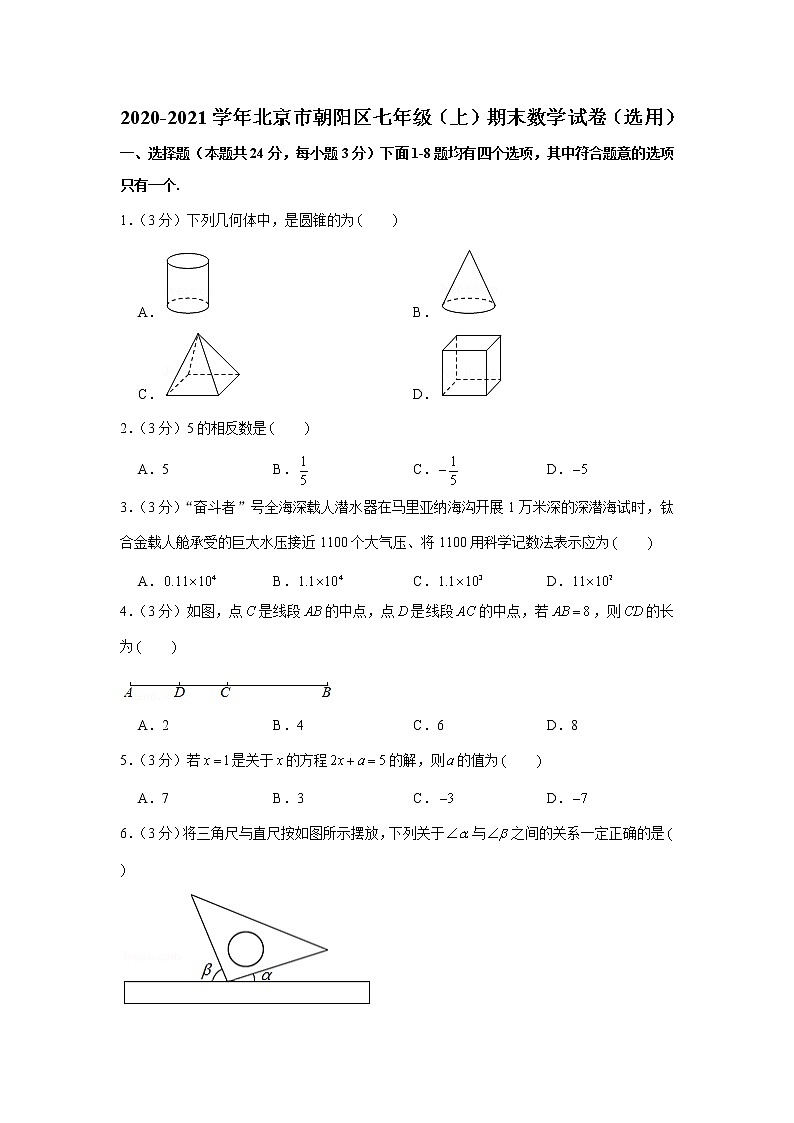
一、选择题（本题共24分，每小题3分）下面1-8题均有四个选项，其中符合题意的选项只有一个.

1．（3分）下列几何体中，是圆锥的为　　

A． B． 

C． D．

2．（3分）5的相反数是　　

A．5 B． C． D．

3．（3分）“奋斗者”号全海深载人潜水器在马里亚纳海沟开展1万米深的深潜海试时，钛合金载人舱承受的巨大水压接近1100个大气压、将1100用科学记数法表示应为　　

A． B． C． D．

4．（3分）如图，点是线段的中点，点是线段的中点，若，则的长为　　

A．2 B．4 C．6 D．8

5．（3分）若是关于的方程的解，则的值为　　

A．7 B．3 C． D．

6．（3分）将三角尺与直尺按如图所示摆放，下列关于与之间的关系一定正确的是　　

A． B． C． D．

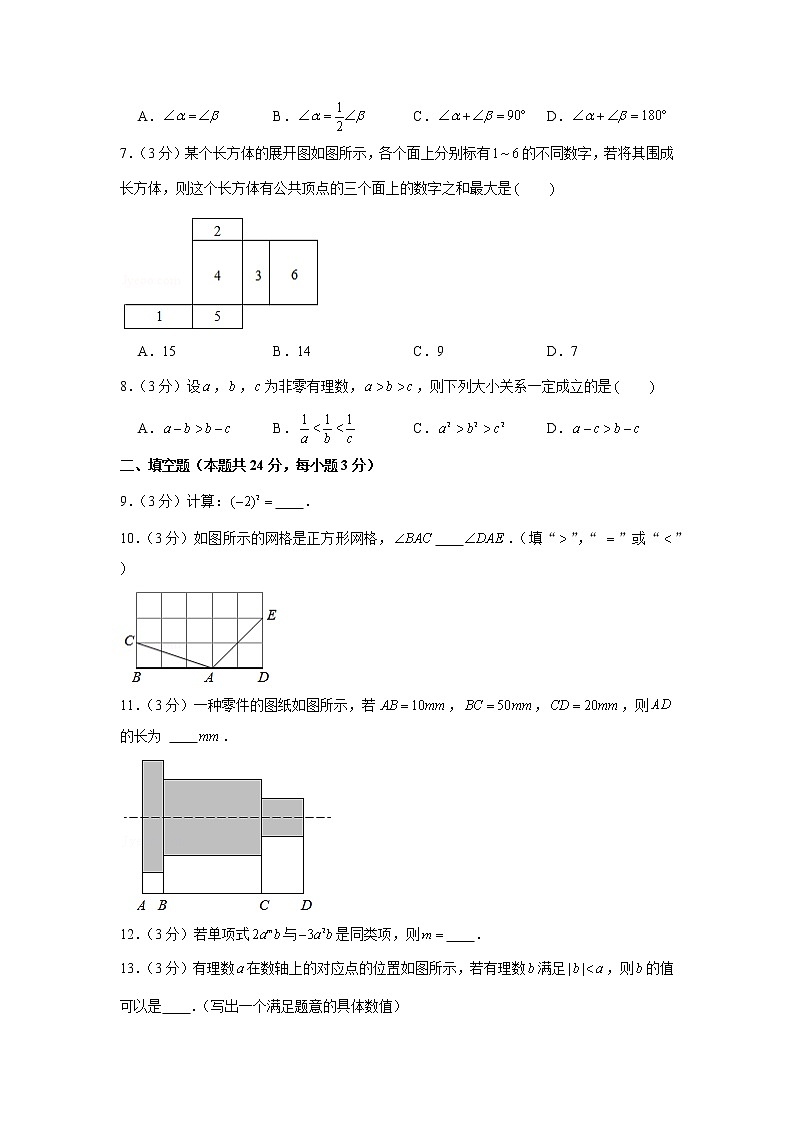
7．（3分）某个长方体的展开图如图所示，各个面上分别标有的不同数字，若将其围成长方体，则这个长方体有公共顶点的三个面上的数字之和最大是　　

A．15 B．14 C．9 D．7

8．（3分）设，，为非零有理数，，则下列大小关系一定成立的是　　

A． B． C． D．

二、填空题（本题共24分，每小题3分）

9．（3分）计算：　　．

10．（3分）如图所示的网格是正方形网格，　　．（填“”，“ ”或“”

11．（3分）一种零件的图纸如图所示，若，，，则的长为 　　．

12．（3分）若单项式与是同类项，则　　．

13．（3分）有理数在数轴上的对应点的位置如图所示，若有理数满足，则的值可以是　　．（写出一个满足题意的具体数值）

14．（3分）如图，在一条笔直的马路（直线两侧各有一个居民区（点，，如果要在这条马路旁建一个购物中心，使购物中心到这两个小区的距离之和最小，那么购物中心应建在线段与直线的交点处，这样做的依据是　　．

15．（3分）用“※”定义一种新运算：对于任意有理数和，※为常数）．例如：2※．若2※的值为3，则的值为　　．

16．（3分）小韩和同学们在一家快餐店吃饭，下表为快餐店的菜单：

小韩记录大家的点餐种类，并根据菜单一次点好，已知他们所点的餐共有11份盖饭，杯饮料和5份小菜，

（1）他们共点了 　　份餐．

（2）若他们至少需要6杯饮料，要使所花费的钱数最少，则应该点 　　份餐．

三、解答题（本题共52分，第17-24题每小题5分，第25、26题每小题5分）

17．（5分）计算：．

18．（5分）计算：．

19．（5分）计算：．

20．（5分）解方程：．

21．（5分）解方程．

22．（5分）已知，求的值．

23．（5分）近年来，我国数字经济规模不断扩张，贡献不断增强，逐渐成为驱动我国经济增长的关键．已知我国2005年与2019年数字经济增加值规模之和为38.4万亿元，2019年数字经济增加值规模比2005年数字经济增加值规模的14倍少0.6万亿元．求我国2005年数字经济增加值规模．

24．（5分）阅读材料：

数学活动课上，小智同学提出一个猜想；把一个三位正整数的百位上的与个位上的数交换位置，十位上的数不变，原数与所得数的差等于99乘原数的百位上的数与个位上的数的差．例如：．

回答问题：

（1）小智的猜想是否正确？若正确，对任意情况进行说明；若不正确，说明理由．

（2）已知一个五位正整数的万位上的数为，个位上的数为，把万位上的数与个位上的数交换位置，其余数位上的数不变，原数与所得数的差等于　　．（用含，的式子表示）

25．（6分）已知，射线在的内部，射线是靠近的三等分线，射线是靠近的三等分线．

（1）若平分，

①依题意补全图1；

②的度数为　　．

（2）当射线绕点在的内部旋转时，的度数是否改变？若不变，求的度数；若改变，说明理由．

26．（6分）在数轴上，点表示的数为1，点表示的数为3．对于数轴上的图形，给出如下定义：为图形上任意一点，为线段上任意一点，如果线段的长度有最小值，那么称这个最小值为图形关于线段的极小距离，记作；如果线段的长度有最大值，那么称这个最大值为图形关于线段的极大距离，记作．

例如：点表示的数为4，则（点，线段，（点，线段．

已知点为数轴原点，点，为数轴上的动点．

（1）（点，线段　　，（点，线段　　；

（2）若点，表示的数分别为，，（线段，线段．求的值；

（3）点从原点出发，以每秒2个单位长度沿轴正方向匀速运动；点从表示数的点出发，第1秒以每秒2个单位长度沿轴正方向匀速运动，第2秒以每秒4个单位长度沿轴负方向匀速运动，第3秒以每秒6个单位长度沿轴正方向匀速运动，第4秒以每秒8个单位长度沿轴负方向匀速运动，，按此规律运动，，两点同时出发，设运动的时间为秒，若（线段，线段小于或等于6，直接写出的取值范围．可以等于

2020-2021学年北京市朝阳区七年级（上）期末数学试卷（选用）

参考答案与试题解析

一、选择题（本题共24分，每小题3分）下面1-8题均有四个选项，其中符合题意的选项只有一个.

1．【解答】解：圆锥是由一个圆形的底面，和一个弯曲的侧面围成的，

因此选项中的几何体符合题意，

故选：．

2．【解答】解：根据相反数的定义：5的相反数是．

故选：．

3．【解答】解：1100用科学记数法表示为，

故选：．

4．【解答】解：点是线段的中点，

，

又点是线段的中点，

，

故选：．

5．【解答】解：是关于的方程的解，

，

解得：．

故选：．

6．【解答】解：，

故选：．

7．【解答】解：根据正方体的表面展开图，有数字5的正方形与有数字6的正方形相对，有数字2的正方形与有数字4的正方形相对，有数字1的正方形与有数字3的正方形相对，

所以相交于同一个顶点的三个面上的数字之和最大的为．

故选：．

8．【解答】解：、当，，时，，不符合题意；

、当，，时，，不符合题意；

、当，，时，，不符合题意；

、，，符合题意．

故选：．

二、填空题（本题共24分，每小题3分）

9．【解答】解：．

10．【解答】解：在中，，

在中，可表示，

，

，

故答案为：．

11．【解答】解：由图可知：．

故答案为：80．

12．【解答】解：单项式与是同类项，

，

故答案为：2．

13．【解答】解：因为，

又因为，

所以的值可以是1（答案不唯一）．

故答案为：1（答案不唯一）．

14．【解答】解：依据是两点之间，线段最短，

故答案为：两点之间，线段最短．

15．【解答】解：※的值为3，

※，

，

解得，

故答案为：4．

16．【解答】解：（1）三种套餐中均包含盖饭且只有餐中含小菜，有5份小菜，

餐中含5杯饮料，

只有餐中不含小菜，

他们点了份餐．

故答案为：．

（2）三种餐中均包含盖饭且只有餐中含小菜，

点了5份餐，

餐，餐都有1份盖饭，

餐，餐共有盖饭份，

餐共有，

一共花费：

，

当时，原式，

（元；

当时，原式，

（元；

当时，原式，

（元；

当时，原式，

（元；

当时，原式，

（元；

当时，原式，

（元．

综上所述，当时，所花费的钱数最少，应该点份餐．

故答案为：；3．

三、解答题（本题共52分，第17-24题每小题5分，第25、26题每小题5分）

17．【解答】解：

．

18．【解答】解：原式

．

19．【解答】解：

．

20．【解答】解：，

，

，

解得：．

21．【解答】解：去分母得：，

去括号得：，

移项得：，

合并得：，

解得：．

22．【解答】解：

，

，

，

原式．

23．【解答】解：设我国2005年数字经济增加值规模为万亿元，

根据题意，得，

解得．

答：我国2005年数字经济增加值规模为2.6万亿元．

24．【解答】解：（1）小智的猜想正确．证明如下：

设一个三位正整数的百位上的数为，十位上的数为，个位上的数为，则

该三位正整数为，新三位正整数为，

因为

，

所以小智的猜想是正确的；

（2）原数与所得数的差等于．

故答案为：．

25．【解答】解：（1）①依题意补全图1

  图1

②，

，

；

（2）的度数不变．

是靠近的三等分线，射线是靠近的三等分线，

，，

，

，

．

26．【解答】解：（1）（点，线段，（点，线段，

故答案为：1，3；

（2）点，表示的数分别为，，

点在点的右侧，，

当在的左侧时，（线段，线段，

解得：，

当在的右侧时，（线段，线段，

解得：，

综上所述，的值为或5；

（3）当时，点表示的数为0，点表示的数为，则，

当时，点表示的数为，点表示的数为，则，

当时，点表示的数为，点表示的数为，则，

解得：，

当时，点表示的数为，点表示的数为，则，

解得：，

当时，点表示的数为，点表示的数为，则或，

解得：，

当时，点表示的数为10，点表示的数为4，则，

当时，点表示的数为，点表示的数为，，

，，

，不符合题意，

综上所述，（线段，线段小于或等于6时，或．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/11/25 19:49:13；用户：初中数学1；邮箱：keda1618@xyh.com；学号：39816508