2020-2021学年1. 相似三角形教课课件ppt

这是一份2020-2021学年1. 相似三角形教课课件ppt，共42页。PPT课件主要包含了知识回顾，想一想，不一定，知识探索，∴△ADE∽△ABC，知识概括，例题解析，试一试，达标检测，解答题等内容，欢迎下载使用。
1、两个边数相同的多边形,如果各边对应_________,各角对应_______,那么这两个多边形相似。
2、相似多边形的______________成比例，________相等。
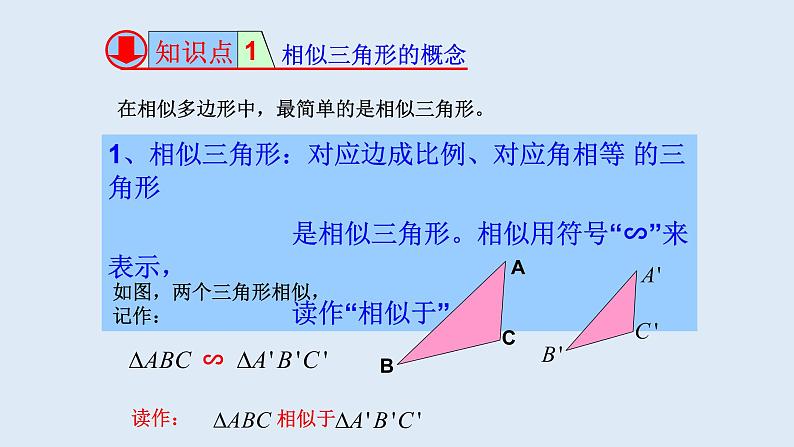
在相似多边形中，最简单的是相似三角形。
1、相似三角形：对应边成比例、对应角相等 的三角形 是相似三角形。相似用符号“∽”来表示， 读作“相似于”。
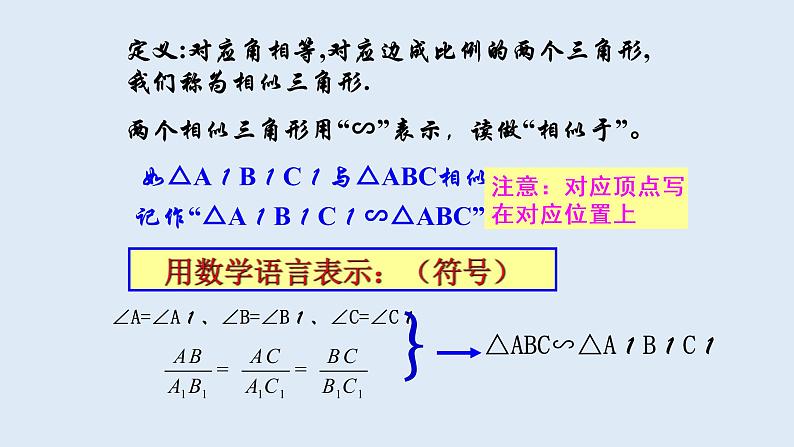
定义:对应角相等,对应边成比例的两个三角形,我们称为相似三角形.两个相似三角形用“∽”表示，读做“相似于”。
∠A=∠A１、∠B=∠B１、∠C=∠C１
用数学语言表示：（符号）
如△A１B１C１与△ABC相似,
注意：对应顶点写 在对应位置上
记作“△A１B１C１∽△ABC”
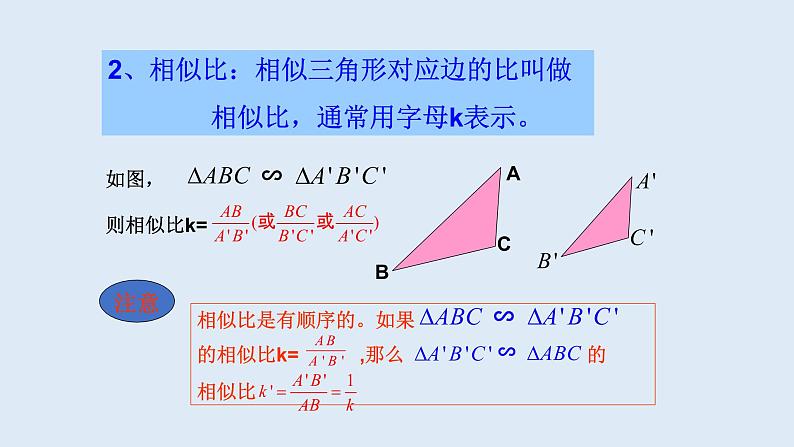
2、相似比：相似三角形对应边的比叫做 相似比，通常用字母k表示。
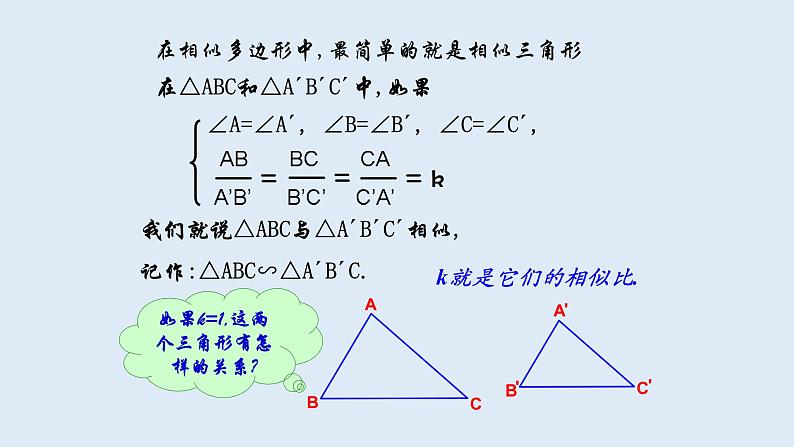
在相似多边形中,最简单的就是相似三角形
在△ABC和△A´B´C´中,如果
∠A=∠A´, ∠B=∠B´, ∠C=∠C´,
我们就说△ABC与△A´B´C´相似,记作:△ABC∽△A´B´C.
如果k=1,这两个三角形有怎样的关系?
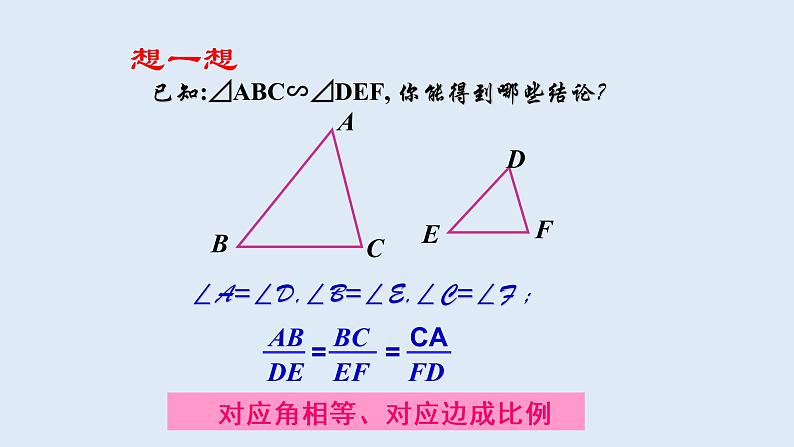
已知:⊿ABC∽⊿DEF, 你能得到哪些结论？
∠A=∠D,∠B=∠E,∠C=∠F ；
对应角相等、对应边成比例
１、两个全等三角形一定相似吗？为什么？２、两个直角三角形一定相似吗？为什么？两个等腰直角三角形呢？３、两个等腰三角形一定相似吗？为什么？两个等边三角形呢？
1.两个全等三角形 相似
2.两个等腰直角三角形 相似
3.两个等边三角形 相似
4.两个直角三角形和两个等腰三角形 相似
1、如图，正方形ABCD的边长为1，点O为对角线的交点，试指出图中的相似三角形。
∴△AOB∽△BOC ∽ △COD ∽ △DOA∽△ABC ∽△BCD ∽ △CDA ∽ △DAB.
2、如果一个三角形的三边长分别为5、12和13，与其相似的三角形的最长边长是39，那么较大三角形的周长是多少？较小三角形与较大三角形周长的比是多少？
你能发现周长之比与相似比有何关系？
较大三角形的周长=15+36+39=90
它们周长的比为：（5+12+13）：90=1:3
（1）有公共角的，公共角是对应角；
如果△ABC∽ △ADE,则∠A的对应角是_____
（2）有对顶角的，对顶角是对应角；
如果△ABC∽ △ADE,则∠BAC的对应角是________
（3）对应角所对的边是对应边，对应角所夹的边是对应边；
（4）对应边所对的角是对应角，对应边所夹的角是对应角；
如果AB对应DF,则∠C=______;
如图，DE∥BC, △ADE与△ABC是否相似？
要说明△ADE∽△ABC，根据定义，就要证明①对应角相等；②对应边成比例。
①在△ADE与△ABC中, ∠A=∠A,∵DE//BC,∴∠ADE=∠B, ∠AED=∠C.
②过点D作DF∥AC交BC于F点。
∵DE∥BC，∴DECF是平行四边形，∴CF=DE
而∠A=∠A,∠ADE=∠B, ∠AED=∠C.
如图，DE∥BC, △ADE与△ABC是否相似？
　　平行于三角形一边的直线，和其他两边（或两边的延长线）相交所构成的三角形与原三角形相似．
∵DE∥BC, ∴△ADE∽ △ABC
如图，在△ABC中，点D是边AB三等分点，DE∥BC,DE=5，求BC的长。
∴△ADE∽ △ABC（ ）
∵点D是边AB三等分点
已知：如图，AB∥EF ∥CD，
图中共有____对相似三角形。
△AOB∽ △FOE
1.如图，在△ABC中，点D是边AB的三等分点，DE//BC，DE=5.求BC的长。
一、填 一填 ：1、如果两个三角形的相似比为1，那么这两个三角形_____2、若△ABC与△A′B′C′相似，一组对应边的长为AB=3 cm，A′B′=4 cm，那么△A′B′C′与△ABC的相似比是____ 3、若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12 cm，那么A′B′C′的最大边长是_____4、已知△ABC的三条边长3cm,4cm,5cm,△ABC∽△A1B1C1，那么△A1B1C1的形状是______，又知△A1B1C1的最大边长为25cm，那么△A1B1C1的面积为
二、认真选一选1、下列命题错误的是（ ）A.两个全等的三角形一定相似 B.两个直角三角形一定相似C.两个相似三角形的对应角相等，对应边成比例D.相似的两个三角形不一定全等2、若△ABC∽△DEF,它们的周长分别为6 cm和8 cm，那么下式中一定成立的是（ ） A.3AB=4DE B.4AC=3DE C.3∠A=4∠D D.4（AB+BC+AC）=3（DE+EF+DF）3、若△ABC与△A′B′C′相似，∠A=55°,∠B=100°，那么∠C’的度数是（ ） A.55° B.100° C.250 D.不能确定4、把△ABC的各边分别扩大为原来的3倍，得到△A′B′C′，下列结论不能成立的是（ ）A.△ABC∽△A′B′C′B.△ABC与△A′B′C′的各对应角相等C.△ABC与△A′B′C′的相似比为 D.△ABC与△A′B′C′的相似比为
1.如果两个三角形全等，则它们必相似。
2.若两个三角形相似，且相似比为1，则它们必全等。
3.如果两个三角形与第三个等腰直角三角形相似， 则这两个三角形必相似。
4.相似的两个三角形一定大小不等。
1.如图，有一块呈三角形形状的草坪，其中一边的长是20m，在这个草坪的图纸上，这条边长5cm，其他两边的长度都是3.5cm。求该草坪其他两边的实际长度。
解：20m=2000cm 设其他两边的实际长度都是x cm，
所以，草坪其他两边的实际长度都是14m
知识点1　相似三角形的相关概念对应边成比例、对应角相等的三角形称为相似三角形．相似用符号“∽”表示，读作“相似于”．注意：根据相似三角形的定义判定两个三角形相似需要注意两点：一是对应边成比例；二是对应角相等，缺一不可．
1．下列命题中，正确的是(　　)A．相似三角形是全等的三角形B．一个角为30°的两个等腰三角形相似C．全等三角形都是相似三角形D．所有等腰直角三角形不一定相似
2．【教材P63练习T2变式】要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5 cm、6 cm和9 cm，另一个三角形的最短边长为2.5 cm，则它的最长边为(　　)A．3 cmB．4 cmC．4.5 cmD．5 cm3．如图，△ADE∽△ABC，相似比为2∶5，若AD＝4，则AB的长为(　　)A．12B．10C．8D．6
7．如图，在△ABC中，DE∥BC，已知CD＝1，BC＝1.8，DE＝1.5，求AD的长．
14．如图，梯形ABCD中，AB∥CD，点F在BC上，DF与AB的延长线交于点G.(1)求证：△CDF∽△BGF；(2)若BF＝2FC，过点F作EF∥CD交AD于点E，若AB＝6，EF＝4，求CD的长．