

所属成套资源:2022年中考数学基础巩固专题复习 (含答案)
2022年中考数学基础巩固专题复习(三)不等式和不等式组 (含答案)
展开
这是一份2022年中考数学基础巩固专题复习(三)不等式和不等式组 (含答案),共13页。
【知识要点】
知识点1、不等式的解:能使不等式成立的未知数的值叫做不等式的解。
知识点2、不等式的解集:一个含有未知数的不等式的解的全体叫做这个不等式的解集。
知识点3、不等式的解集在数轴上的表示:
(1)x>a:数轴上表示a的点画成空心圆圈,表示a的点的右边部分来表示;
(2)x<a:数轴上表示a的点画成空心圆圈,表示a的点的左边部分来表示;
(3)x≥a:数轴上表示a的点画成实心圆点,表示a的点及表示a的点的右边部分来表示;
(4)x≤a:数轴上表示a的点画成实心圆点,表示a的点及表示a的点的左边部分来表示。
在数轴上表示大于3的数的点应该是数3所对应点的右边。画图时要注意方向(向右)和端点(不包括数3,在对应点画空心圆圈)。如图所示:
SKIPIF 1 < 0
同样,如果某个不等式的解集为x≤-2, 那么它表示x取-2左边的点
画实心圆点。如图所示:
SKIPIF 1 < 0
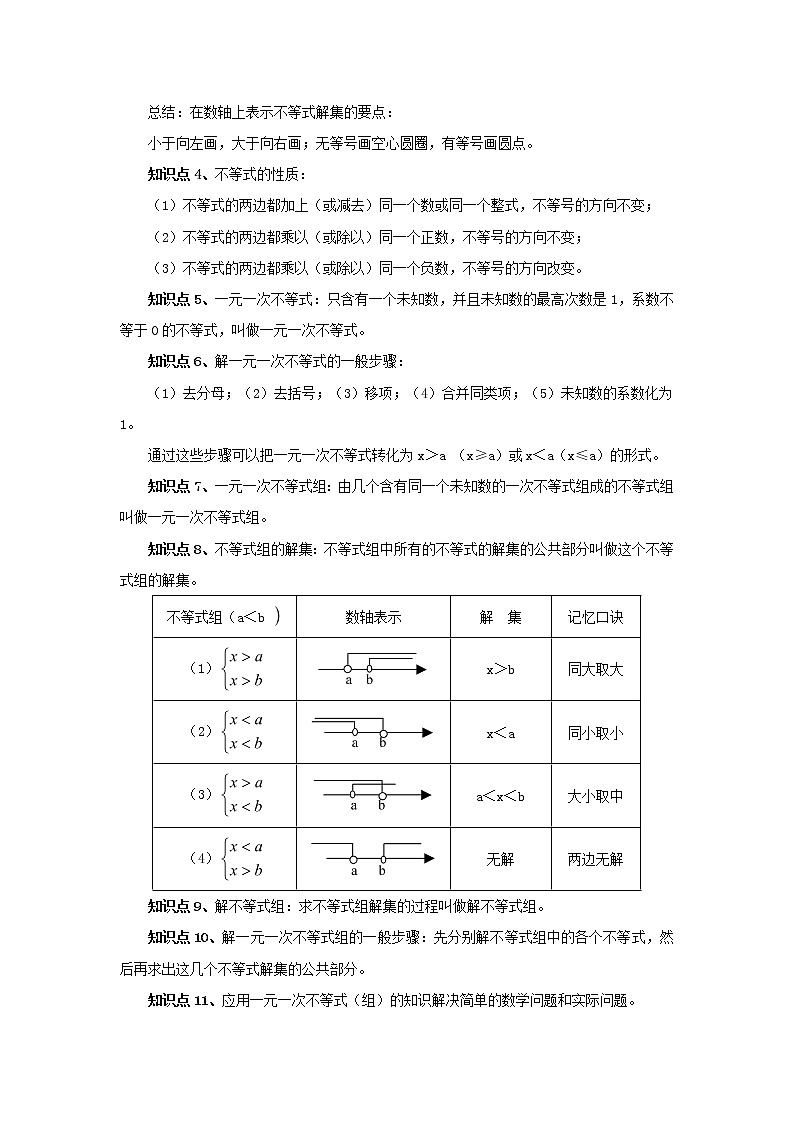
总结:在数轴上表示不等式解集的要点:
小于向左画,大于向右画;无等号画空心圆圈,有等号画圆点。
知识点4、不等式的性质:
(1)不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变;
(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
知识点5、一元一次不等式:只含有一个未知数,并且未知数的最高次数是1,系数不等于0的不等式,叫做一元一次不等式。
知识点6、解一元一次不等式的一般步骤:
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)未知数的系数化为1。
通过这些步骤可以把一元一次不等式转化为x>a (x≥a)或x<a(x≤a)的形式。
知识点7、一元一次不等式组:由几个含有同一个未知数的一次不等式组成的不等式组叫做一元一次不等式组。
知识点8、不等式组的解集:不等式组中所有的不等式的解集的公共部分叫做这个不等式组的解集。
知识点9、解不等式组:求不等式组解集的过程叫做解不等式组。
知识点10、解一元一次不等式组的一般步骤:先分别解不等式组中的各个不等式,然后再求出这几个不等式解集的公共部分。
知识点11、应用一元一次不等式(组)的知识解决简单的数学问题和实际问题。
【复习点拨】
1. 理解不等式,不等式的解等概念,会在数轴上表示不等式的解;
2. 理解不等式的基本性质,会应用不等式的基本性质进行简单的不等式变形,会解一元一次不等式;
3. 理解一元一次不等式组和它的解的概念,会解一元一次不等式组;
4. 能应用一元一次不等式(组)的知识分析和解决简单的数学问题和实际问题。
【典例解析】
例题1:(山东枣庄)x取哪些整数值时,不等式5x+2>3(x﹣1)与x≤2﹣都成立?
【考点】C7:一元一次不等式的整数解.
【分析】根据题意分别求出每个不等式解集,根据口诀:大小小大中间找,确定两不等式解集的公共部分,即可得整数值.
【解答】解:根据题意解不等式组,
解不等式①,得:x>﹣,
解不等式②,得:x≤1,
∴﹣<x≤1,
故满足条件的整数有﹣2、﹣1、0、1.
例题2:(甘肃张掖)估计与0.5的大小关系是: > 0.5.(填“>”、“=”、“<”)
【考点】2A:实数大小比较.
【分析】首先把两个数采用作差法相减,根据差的正负情况即可比较两个实数的大小.
【解答】解:∵﹣0.5=﹣=,
∵﹣2>0,
∴>0.
答:>0.5.
例题3:(·青海西宁·3分)某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )
A.103块 B.104块 C.105块 D.106块
【考点】一元一次不等式的应用.
【分析】根据题意设出未知数,列出相应的不等式,从而可以解答本题.
【解答】解:设这批手表有x块,
550×60+(x﹣60)×500>55000
解得,x>104
∴这批电话手表至少有105块,
故选C.
例题4:(江西)解不等式组:,并把解集在数轴上表示出来.
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.
【分析】分别求出每一个不等式的解集,根据解集在数轴上的表示即可确定不等式组的解集.
【解答】解:解不等式﹣2x<6,得:x>﹣3,
解不等式3(x﹣2)≤x﹣4,得:x≤1,
将不等式解集表示在数轴如下:
则不等式组的解集为﹣3<x≤1
例题5:(浙江义乌)(1)计算:(2﹣π)0+|4﹣3|﹣.
(2)解不等式:4x+5≤2(x+1)
【考点】C6:解一元一次不等式;2C:实数的运算;6E:零指数幂.
【分析】(1)原式利用零指数幂法则,绝对值的代数意义,以及二次根式性质计算即可得到结果;
(2)去括号,移项,合并同类项,系数化成1即可求出不等式的解集.
【解答】解:(1)原式=1
=﹣3;
(2)去括号,得4x+5≤2x+2
移项合并同类项得,2x≤﹣3
解得x.
例题6:.(湖北宜昌)解不等式组.
【考点】CB:解一元一次不等式组.
【分析】分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
【解答】解:,
由①得:x≥﹣2,
由②得:x<2,
故不等式组的解集为﹣2≤x<2.
例题7:(张家界)先化简(1﹣)÷,再从不等式2x﹣1<6的正整数解中选一个适当的数代入求值.
【考点】6D:分式的化简求值;C7:一元一次不等式的整数解.
【分析】先把括号里的式子进行通分,再把后面的式子根据完全平方公式、平方差公式进行因式分解,然后约分,再求出不等式的解集,最后代入一个合适的数据代入即可.
【解答】解:(1﹣)÷=×=,
∵2x﹣1<6,
∴2x<7,
∴x<,
把x=3代入上式得:
原式==4.
例题8:(甘肃张掖)解不等式组,并写出该不等式组的最大整数解.
【考点】CC:一元一次不等式组的整数解;CB:解一元一次不等式组.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解≤1得:x≤3,
解1﹣x<2得:x>﹣1,
则不等式组的解集是:﹣1<x≤3.
∴该不等式组的最大整数解为x=3.
【达标检测】
一、选择题
1. (湖南株洲)
已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>bB.a+2>b+2C.﹣a<﹣bD.2a>3b
【考点】C2:不等式的性质.
【分析】根据不等式的性质即可得到a>b,a+2>b+2,﹣a<﹣b.
【解答】解:由不等式的性质得a>b,a+2>b+2,﹣a<﹣b.
故选D.
2. (四川眉山)不等式﹣2x>的解集是( )
A.x<﹣B.x<﹣1C.x>﹣D.x>﹣1
【考点】C6:解一元一次不等式.
【分析】根据不等式的基本性质两边都除以﹣2可得.
【解答】解:两边都除以﹣2可得:x<﹣,
故选:A.
3. (·云南省昆明市·4分)不等式组的解集为( )
A.x≤2 B.x<4 C.2≤x<4 D.x≥2
【考点】解一元一次不等式组.
【分析】先求出每个不等式的解集,再根据口诀:大小小大中间找确定不等式组的解集即可.
【解答】解:解不等式x﹣3<1,得:x<4,
解不等式3x+2≤4x,得:x≥2,
∴不等式组的解集为:2≤x<4,
故选:C.
4. (山东临沂)不等式组中,不等式①和②的解集在数轴上表示正确的是( )
A.B.C.D.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式①,得:x<1,
解不等式②,得:x≥﹣3,
则不等式组的解集为﹣3≤x<1,
故选:B.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键
5. (·山东省滨州市·3分)对于不等式组下列说法正确的是( )
A.此不等式组无解
B.此不等式组有7个整数解
C.此不等式组的负整数解是﹣3,﹣2,﹣1
D.此不等式组的解集是﹣<x≤2
【考点】一元一次不等式组的整数解;解一元一次不等式组.
【分析】分别解两个不等式得到x≤4和x>﹣2.5,利用大于小的小于大的取中间可确定不等式组的解集,再写出不等式组的整数解,然后对各选项进行判断.
【解答】解:,
解①得x≤4,
解②得x>﹣2.5,
所以不等式组的解集为﹣2.5<x≤4,
所以不等式组的整数解为﹣2,﹣1,0,1,2,3,4.
故选B.
二、填空题:
6. (浙江衢州)二次根式中字母a的取值范围是 a≥2 .
【考点】72:二次根式有意义的条件.
【分析】由二次根式中的被开方数是非负数,可得出a﹣2≥0,解之即可得出结论.
【解答】解:根据题意得:a﹣2≥0,
解得:a≥2.
故答案为:a≥2.
7. (张家界)不等式组的解集是 x≥1 .
【考点】C3:不等式的解集.
【分析】直接利用不等式组的解集确定方法得出答案.
【解答】解:不等式组的解集是:x≥1.
故答案为:x≥1.
8. (湖南岳阳)不等式组的解集是 x<﹣3 .
【分析】先求出每个不等式的解集,再求出不等式组的解集即可.
【解答】解:
∵解不等式①得:x≤3,
解不等式②得:x<﹣3,
∴不等式组的解集为x<﹣3,
故答案为:x<﹣3.
【点评】本题考查了解一元一次不等式和解一元一次不等式组,能根据不等式的解集求出不等式组的解集是解此题的关键.
9. (湖南株洲)
已知“x的3倍大于5,且x的一半与1的差不大于2”,则x的取值范围是 <x≤6 .
【考点】C6:解一元一次不等式.
【分析】根据题意列出不等式组,再求解集即可得到x的取值范围.
【解答】解:依题意有,
解得<x≤6.
故x的取值范围是<x≤6.
故答案为:<x≤6.
10. (·黑龙江龙东·3分)不等式组有3个整数解,则m的取值范围是 2<x≤3 .
【考点】一元一次不等式组的整数解.
【分析】首先确定不等式组的整数解,然后根据只有这三个整数解即可确定.
【解答】解:不等式的整数解是0,1,2.则m的取值范围是2<x≤3.
故答案是:2<x≤3.
(·陕西·3分)不等式﹣x+3<0的解集是 x>6 .
【考点】解一元一次不等式.
【分析】移项、系数化成1即可求解.
【解答】解:移项,得﹣x<﹣3,
系数化为1得x>6.
故答案是:x>6.
三、解答题
11. (年江苏扬州)解不等式组,并求出它的所有整数解.
【考点】CC:一元一次不等式组的整数解;CB:解一元一次不等式组.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式2x+3≥0,得:x≥﹣1.5,
解不等式5﹣x>0,得:x<3,
则不等式组的解集为﹣1.5≤x<3,
∴不等式组的整数解为﹣1、0、1、2.
12. 解不等式:.
【考点】解一元一次不等式.
【分析】根据去分母,去括号,移项,合并同类项,系数化为1等步骤解不等式
【解答】解:
SKIPIF 1 < 0
∴不等式组的解集为 SKIPIF 1 < 0
13. (·黑龙江龙东·10分)某中学开学初到商场购买A、B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元,已知购买一个B种品牌的足球比购买一个A钟品牌的足球多花30元.
(1)求购买一个A种品牌、一个B种品牌的足球各需多少元.
(2)学校为了响应习总书记“足球进校园”的号召,决定再次购进A、B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高4元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买的B种品牌足球不少于23个,则这次学校有哪几种购买方案?
(3)请你求出学校在第二次购买活动中最多需要多少资金?
【考点】一元一次不等式组的应用;二元一次方程组的应用.
【分析】(1)设A种品牌足球的单价为x元,B种品牌足球的单价为y元,根据“总费用=买A种足球费用+买B种足球费用,以及B种足球单价比A种足球贵30元”可得出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)设第二次购买A种足球m个,则购买B中足球(50﹣m)个,根据“总费用=买A种足球费用+买B种足球费用,以及B种足球不小于23个”可得出关于m的一元一次不等式组,解不等式组可得出m的取值范围,由此即可得出结论;
(3)分析第二次购买时,A、B种足球的单价,即可得出那种方案花钱最多,求出花费最大值即可得出结论.
【解答】解:(1)设A种品牌足球的单价为x元,B种品牌足球的单价为y元,
依题意得:,解得:.
答:购买一个A种品牌的足球需要50元,购买一个B种品牌的足球需要80元.
(2)设第二次购买A种足球m个,则购买B中足球(50﹣m)个,
依题意得:,
解得:25≤m≤27.
故这次学校购买足球有三种方案:
方案一:购买A种足球25个,B种足球25个;
方案二:购买A种足球26个,B种足球24个;
方案三:购买A种足球27个,B种足球23个.
(3)∵第二次购买足球时,A种足球单价为50+4=54(元),B种足球单价为80×0.9=72(元),
∴当购买方案中B种足球最多时,费用最高,即方案一花钱最多.
∴25×54+25×72=3150(元).
答:学校在第二次购买活动中最多需要3150元资金.
3.(·湖北荆门·5分)解不等式组.
【考点】解一元一次不等式组.
【分析】首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
【解答】解①得x>﹣,
解②得x≤0,
则不等式组的解集是﹣<x≤0.
14. (·重庆市B卷·4分)如果关于x的分式方程﹣3=有负分数解,且关于x的不等式组的解集为x<﹣2,那么符合条件的所有整数a的积是( )
A.﹣3B.0C.3D.9
【考点】解一元一次不等式组;解分式方程.
【专题】计算题;分式方程及应用;一元一次不等式(组)及应用.
【分析】把a看做已知数表示出不等式组的解,根据已知解集确定出a的范围,分式方程去分母转化为整式方程,将a的整数解代入整式方程,检验分式方程解为负分数确定出所有a的值,即可求出之积.
【解答】解:,
由①得:x≤2a+4,
由②得:x<﹣2,
由不等式组的解集为x<﹣2,得到2a+4≥﹣2,即a≥﹣3,
分式方程去分母得:a﹣3x﹣3=1﹣x,
把a=﹣3代入整式方程得:﹣3x﹣6=1﹣x,即x=﹣,符合题意;
把a=﹣2代入整式方程得:﹣3x﹣5=1﹣x,即x=﹣3,不合题意;
把a=﹣1代入整式方程得:﹣3x﹣4=1﹣x,即x=﹣,符合题意;
把a=0代入整式方程得:﹣3x﹣3=1﹣x,即x=﹣2,不合题意;
把a=1代入整式方程得:﹣3x﹣2=1﹣x,即x=﹣,符合题意;
把a=2代入整式方程得:﹣3x﹣1=1﹣x,即x=1,不合题意;
把a=3代入整式方程得:﹣3x=1﹣x,即x=﹣,符合题意;
把a=4代入整式方程得:﹣3x+1=1﹣x,即x=0,不合题意,
∴符合条件的整数a取值为﹣3;﹣1;1;3,之积为9,
故选D
【点评】此题考查了解一元一次不等式组,以及解分式方程,熟练掌握运算法则是解本题的关键.
15. (重庆B)若数a使关于x的不等式组有且仅有四个整数解,且使关于y的分式方程+=2有非负数解,则所以满足条件的整数a的值之和是( )
A.3B.1C.0D.﹣3
【分析】先解不等式组,根据不等式组有且仅有四个整数解,得出a≤3,再解分式方程+=2,根据分式方程有非负数解,得到a≥﹣2,进而得到满足条件的整数a的值之和.
【解答】解:解不等式组,可得,
∵不等式组有且仅有四个整数解,
∴﹣≥﹣1,
∴a≤3,
解分式方程+=2,可得y=(a+2),
又∵分式方程有非负数解,
∴y≥0,
即(a+2)≥0,
解得a≥﹣2,
∴﹣2≤a≤3,
∴满足条件的整数a的值为﹣2,﹣1,0,1,2,3,
∴满足条件的整数a的值之和是3,
故选:A.
【点评】本题主要考查了分式方程的解,解题时注意:使分式方程中令等号左右两边相等且分母不等于0的未知数的值,这个值叫方程的解.
不等式组(a<b SKIPIF 1 < 0
数轴表示
解 集
记忆口诀
(1) SKIPIF 1 < 0
SKIPIF 1 < 0
x>b
同大取大
(2) SKIPIF 1 < 0
SKIPIF 1 < 0
x<a
同小取小
(3) SKIPIF 1 < 0
SKIPIF 1 < 0
a<x<b
大小取中
(4) SKIPIF 1 < 0
SKIPIF 1 < 0
无解
两边无解
相关试卷
这是一份不等式与不等式组专题复习(可用于中考 含答案),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份初中数学中考复习 专题09 不等式与不等式组(解析版),共23页。试卷主要包含了不等式的解,不等式的解集,不等式的性质,5,b=0,4,等内容,欢迎下载使用。
这是一份初中数学中考复习 专题03 不等式与不等式组(解析版),共33页。









