2021年福建省三明市九年级上学期数学期中试卷 (1)含答案

这是一份2021年福建省三明市九年级上学期数学期中试卷 (1)含答案，共15页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

 九年级上学期数学期中试卷
一、单项选择题
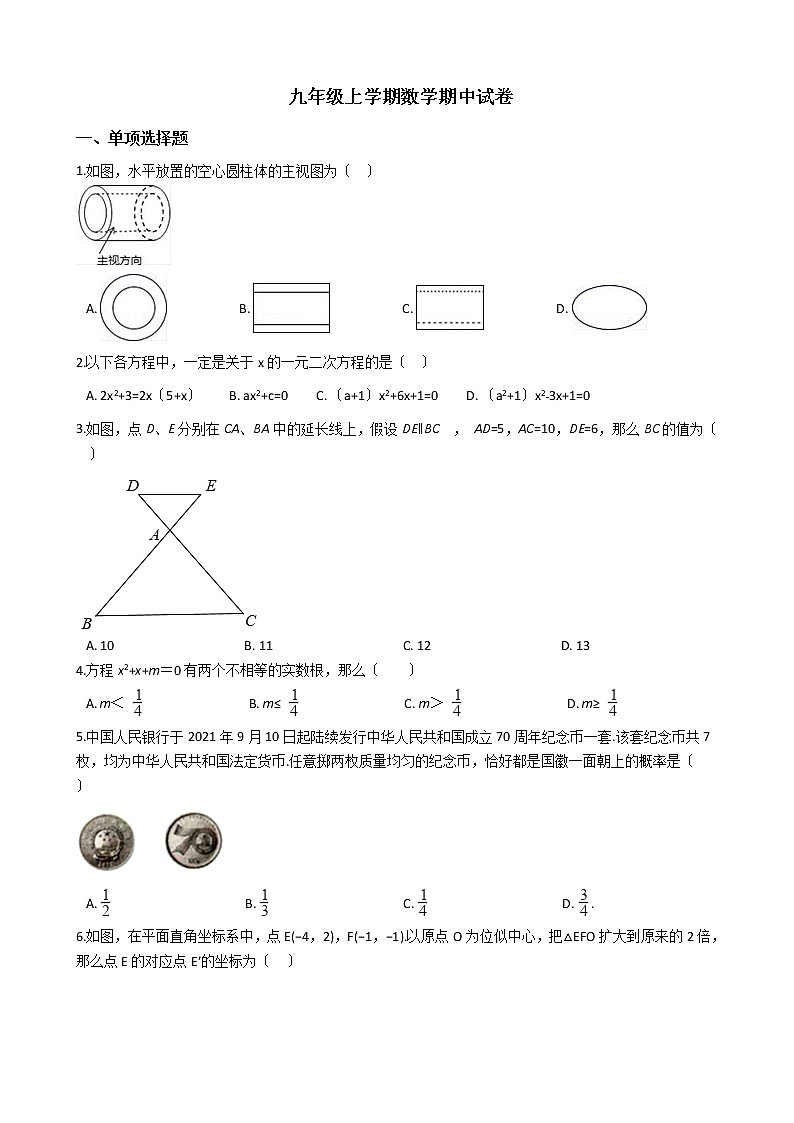
1.如图，水平放置的空心圆柱体的主视图为〔   〕

A.                       B.                       C.                       D. 
2.以下各方程中，一定是关于x的一元二次方程的是〔   〕
A. 2x2+3=2x〔5+x〕        B. ax2+c=0        C. 〔a+1〕x2+6x+1=0        D. 〔a2+1〕x2﹣3x+1=0
3.如图，点D、E分别在CA、BA中的延长线上，假设DE∥BC ， AD=5，AC=10，DE=6，那么BC的值为〔   〕

A. 10                                         B. 11                                         C. 12                                         D. 13
4.方程x2+x+m＝0有两个不相等的实数根，那么〔　　〕
A. m＜                                 B. m≤                                 C. m＞                                 D. m≥
5.中国人民银行于2021年9月10日起陆续发行中华人民共和国成立70周年纪念币一套.该套纪念币共7枚，均为中华人民共和国法定货币.任意掷两枚质量均匀的纪念币，恰好都是国徽一面朝上的概率是〔    〕
    
A.                                          B.                                          C.                                          D. .
6.如图，在平面直角坐标系中，点E(−4，2)，F(−1，−1).以原点O为位似中心，把△EFO扩大到原来的2倍，那么点E的对应点E′的坐标为〔    〕

A. (−8，4)                   B. (8，−4)                   C. (8，4)或(−8，−4)                   D. (−8，4)或(8，−4)
7.以下命题中，正确的选项是〔       〕
A. 菱形的对角线相等                                              B. 平行四边形既是轴对称图形，又是中心对称图形
C. 正方形的对角线不能相等                                   D. 正方形的对角线相等且互相垂直
8.目前，支付宝平台入驻了不少的理财公司，推出了一些理财产品.李阿姨用10000元本金购置了一款理财产品，到期后自动续期，两期结束后共收回本息10926元设此款理财产品每期的平均收益率为x，那么根据题意可得方程〔    〕
A.                                     B. 
C.                                    D. 
9.太原是我国生活垃圾分类的46个试点城市之一，垃圾分类的强制实施也即将提上日程根据规定，我市将垃圾分为了四类可回收垃圾、餐厨垃圾有害垃圾和其他垃圾现有投放这四类垃圾的垃圾桶各1个，假设将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶，投放正确的概率是〔    〕
              
A.                                         B.                                         C.                                         D. 
10.如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，那么四边形AECF形状的变化依次为〔   〕

A. 平行四边形→正方形→平行四边形→矩形           B. 平行四边形→菱形→平行四边形→矩形
C. 平行四边形→正方形→菱形→矩形                      D. 平行四边形→菱形→正方形→矩形
二、填空题
11. ＝ 〔b+d≠0〕，那么 的值为________ ．
12.方程 的两个根是等腰三角形的底和腰，那么这个等腰三角形周长是________．
13.菱形的面积为24，一条对角线长为6，那么这个菱形的另一条对角线长是________．
14.在同一时刻，身高1.6m的小强的影长是1.2m，旗杆的影长是15m，那么旗杆高为________.
15.x1 ， x2是方程x2-3x-1=0的两根，那么 =________．
16.如图，把矩形ABCD沿EF翻转，点B恰好落在AD边的B′处，假设AE=2，DE=6，∠EFB=60°，那么矩形ABCD的面积是 ________

三、解答题
17.解方程：x2﹣5x+6＝0
18.解方程： 2(x－3)2＝x2－9
19.如图，□ABCD的对角线AC，BD相交于点O，EF过点O且与AD，BC分别相交于点E，F．求证：OE=OF．

20.如图，在正方形ABCD中，点P是对角线AC上一点，连接PB、PD，点E在BC的延长线上，且PE＝PB．

求证：
〔1〕△BCP ≌△DCP；
〔2〕∠DPE ＝∠ABC．
21.百货商店销售某种冰箱，每台进价2500元．市场调研说明：当每台售价为2900元时，平均每天能售出8台；每台售价每降低10元，平均每天能多售出1台．(销售利润＝销售价－进价)
〔1〕如果每台冰箱降价100元，那么每台冰箱的销售利润为________元，平均每天可销售冰箱________台；
〔2〕商店想要使这种冰箱平均每天的销售利润到达5600元，且尽可能地减少冰箱库存，每台冰箱应降价多少元？
22.△ABC如下列图，点D ， E ， F分别在边AB ， BC ， AC上，四边形BEFD是菱形．

〔1〕请你在图中作出正确的菱形BEFD；〔要求尺规作图，并保存作图痕迹〕
〔2〕证明你所画的四边形BEFD是菱形．
23.为了解某校落实新课改精神的情况，现以该校九年级二班的同学参加课外活动的情况为样本，对其参加“球类〞、“绘画类〞、“舞蹈类〞、“音乐类〞、“棋类〞活动的情况进行调查统计，并绘制了如下列图的统计图．

〔1〕参加音乐类活动的学生人数为________人，参加球类活动的人数的百分比为________；
〔2〕请把图2〔条形统计图〕补充完整；
〔3〕该校学生共800人，那么参加棋类活动的人数约为________；
〔4〕该班参加舞蹈类活动的4位同学中，有1位男生〔用E表示〕和3位女生〔分别用F ， G ， H表示〕，先准备从中选取两名同学组成舞伴，请用列表或画树状图的方法求恰好选中一男一女的概率．
24.如图，在矩形ABCD中，点的P在AD上，AB＝2，AP＝1，PE⊥PF ， 点E在AB上，点F在BC上，连接EF ．

〔1〕当点E与点B重合时，点F恰好与点C重合〔如图2〕，求PC的长；
〔2〕将直角∠EPF从图2中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止，在这个过程中，请解答以下问题：
①判断  的值是否发生变化，并说明理由；
②直接写出从开始到停止，线段EF的中点经过的路径的长．
25.如图1，在△ABC中，AD⊥BC，DE⊥AB ， DF⊥AC．

〔1〕假设AD 2 ＝BD·DC，
①求证：∠BAC ＝90°；
②连接EF，假设AB ＝4，DC ＝6，求EF．
〔2〕如图2，假设AD ＝4，BD ＝2，DC ＝4，求EF．

答案解析局部
一、单项选择题
1.【答案】 C
【解析】【解答】水平放置的空心圆柱的主视图是矩形，中间有两条画虚线，
故答案为：C．

【分析】根据三视图的定义逐项判定即可。
2.【答案】 D
【解析】【解答】解：A、由2x2+3=2x〔5+x〕得到：10x﹣3=0，不是一元二次方程，故本选项错误；
B、当a=0时，ax2+c=0不是一元二次方程，故本选项错误；
C、当a+1=0时，〔a+1〕x2+6x+1=0不是一元二次方程，故本选项错误；
D、由a2+1＞0知〔a2+1〕x2﹣3x+1=0是一元二次方程，故本选项正确；
应选：D．
【分析】根据一元二次方程的定义进行判断．
3.【答案】 C
【解析】【解答】解：∵DE∥BC，
∴∠E=∠B，∠D=∠C，
∴△EAD∽△CAB，
∴AC：AD=BC：DE，
∵AD=5，AC=10，DE=6，
∴10：5=BC：6．
∴BC=12．
故答案为：C．

【分析】根据DE∥BC，证出△EAD∽△CAB，，再利用相似三角形的性质列出比例式求解即可。
4.【答案】 A
【解析】【解答】解：∵方程x2+x+m＝0有两个不相等的实数根，
∴1-4m>0，
∴m< ．
故答案为：A．
【分析】根据∆>0列不等式求解即可．
5.【答案】 C
【解析】【解答】解：掷一枚质量均匀的纪念币，恰好是国徽一面朝上的概率是 ，
∴掷两枚质量均匀的纪念币，恰好都是国徽一面朝上的概率是： ；
故答案为：C.
【分析】根据等可能事件的可能性，计算概率即可得到答案.
6.【答案】 D
【解析】【解答】∵以原点O为位似中心，把△EFO扩大到原来的2倍，点E〔−4，2〕，
∴点E的对应点E'的坐标为〔−4×2，2×2〕或〔4×2，−2×2〕，即〔−8，4〕或〔8，−4〕，
故答案为：D．

【分析】根据相似图形的性质求解即可。
7.【答案】 D
【解析】【解答】解：A.菱形的对角线不一定相等， A 不符合题意；
B.平行四边形不是轴对称图形，是中心对称图形，B 不符合题意；
C. 正方形的对角线相等，C不符合题意；
D.正方形的对角线相等且互相垂直，D 符合题意；
故答案为：D．
【分析】根据菱形，平行四边形，正方形的性质定理判断即可．
8.【答案】 B
【解析】【解答】解：根据题意，设此款理财产品每期的平均收益率为x，那么
；
故答案为：B.
【分析】根据题意，找出等量关系列出方程，即可得到答案.
9.【答案】 C
【解析】【解答】解：由列表法，得：

∴共有12种等可能的结果数，其中将两包垃圾随机投放到其中的两个垃圾箱中，能实现对应投放的结果为1种，
∴投放正确的概率为： ；
故答案为：C.
【分析】根据题意，由列表法得到投放的所有结果，然后正确的只有1种，即可求出概率.
10.【答案】 B
【解析】【解答】解：观察图形可知，四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形.
故答案为：B.
【分析】根据对称中心的定义，根据矩形的性质，可得四边形AECF形状的变化情况.
二、填空题
11.【答案】
【解析】【解答】∵ ＝
∴
∴
故答案为

【分析】根据条件求出ab、cd之间的关系，再代入计算即可。
12.【答案】 10
【解析】【解答】解方程： ，
得 ， ，
当2为腰，4为底时，不能构成等腰三角形；
当4为腰，2为底时，能构成等腰三角形，周长为 ．
故答案为：10．

【分析】先求出一元二次方程的解，在根据等腰三角形的性质及三角形三边的关系求解即可。
13.【答案】 8
【解析】【解答】解：如下列图：∵S菱形ABCD＝24，

∴ BD·AC＝24，
∵AC＝6，
∴ BD·6＝24，
∴BD＝8，
故答案为：8．

【分析】利用菱形的性质：菱形的面积等于对角线乘积的一半求解即可。
14.【答案】 20
【解析】【解答】解：根据题意可得：设旗杆高为x.
根据在同一时刻身高与影长成比例可得： = ，
故x=20m.
故答案为20.
【分析】利用在同一时刻身高与影长成比例计算.
15.【答案】 ﹣3
【解析】【解答】∵ ， 是方程 的两根，∴ 、 ，∴ = = =﹣3．故答案为﹣3．
【分析】将分式进行运算，根据一元二次方程根与系数的关系进行作答即可。
16.【答案】
【解析】【解答】如图，连接BE，

∵在矩形ABCD中，AD∥BC，∠EFB=60°，
∴∠AEF=180°-∠EFB=180°－60°=120°，∠DEF=∠EFB=60°.
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处，∴∠BEF=∠DEF=60°.
∴∠AEB=∠AEF-∠BEF=120°－60°=60°. ∴∠ABE=30°.
∴在Rt△ABE中，AB= 2 .
∵AE=2，DE=6，∴AD=AE+DE=2+6=8.
∴矩形ABCD的面积=AB•AD=2 ×8=16 .
故答案为：D.

【分析】根据翻折及矩形的性质可得：∠EFB=60°，可证出∠DEF=∠EFB=60°，在Rt△ABE中，利用30°.所对的直角边等于斜边的一半求出AB，再求出AD，最后利用矩形的面积计算即可。
三、解答题
17.【答案】 利用因式分解法求解可得．
解：∵x2﹣5x+6＝0，
∴〔x﹣2〕〔x﹣3〕＝0，
那么x﹣2＝0或x﹣3＝0，
解得x1＝2，x2＝3．
【解析】【分析】利用因式分解的方法解出方程即可.
18.【答案】 解：2(x－3)2＝x2－9
2(x-3)2-(x+3)(x-3)=0
(x-3)(2x-6-x-3)=0
x1=3，x2=9．
【解析】【分析】移项，利用因式分解法求解即可。
19.【答案】 证明：∵四边形ABCD是平行四边形，
∴OA=OC，AD∥BC，
∴∠OAE=∠OCF，
在△OAE和△OCF中，
 
∴△AOE≌△COF〔ASA〕，
∴OE=OF．

【解析】【分析】利用平行四边形的性质得到角、边相等，再利用“ASA〞证明△AOE≌△COF，得出结论。
20.【答案】 〔1〕证明：∵四边形ABCD是正方形
∴BC=DC，∠ACB ＝∠ACD ，∠ABC ＝ 90°
又∵PC = PC
∴△BCP ≌△DCP．


〔2〕证明：∵PE＝PB，
∴∠E ＝∠PBE ，
∵△BCP ≌△DCP ，
∴∠PBE ＝∠PDC ，
∴∠E ＝∠PDC ，
∵∠E ＋∠1 ＝ 90°，∠1 ＝ ∠2
∴∠PDC ＋∠2 ＝ 90°
即∠DPE ＝ 90°
∴∠DPE ＝∠ABC．
【解析】【分析】〔1〕根据正方形的四条边都相等可得BC=DC，对角线平分一组对角得角相等，再利用“SAS〞证明全等即可；〔2〕根据全等三角形对应边、角相等，再根据平行线的性质证明即可。
21.【答案】 〔1〕300；18
〔2〕解：设每台冰箱应降价x元，
由题意得： ，
解得 ，
当 时，每天可销售冰箱的数量为 〔台〕，
当 时，每天可销售冰箱的数量为 〔台〕，
因为商店想要尽可能地减少冰箱库存，
所以 ，
答：每台冰箱应降价200元．
【解析】【解答】〔1〕每台冰箱的销售利润为 〔元〕，
平均每天可销售冰箱的数量为 〔台〕，
故答案为：300，18；

【分析】〔1〕利用降价后的销售价减去进价可得每台冰箱的销售利润，降价100元可增加10台，再加上8台即可；〔2〕根据“总利润=每台的销售利润销售量〞建立方程求解即可。
22.【答案】 〔1〕解：如图，BEFD就是正确的菱形．


〔2〕证明：由〔1〕可知，
BF是∠ABC的角平分线
∴∠ABF =∠CBF
∵DE是线段BF的垂直平分线
∴DB = DF，EB = EF
∴∠DBF =∠DFB，∠EBF =∠EFB
∴∠CBF =∠DFB，∠ABF =∠EFB
∴DF∥BC，EF∥AB
∴四边形BEFD是平行四边形
又∵DB =DF
∴四边形BEFD是菱形．
【解析】【分析】〔1〕作三角形ABC的角平分线交AC于点F，再作线段BF的垂直平分线交AB于点D，交BC于点E，连接DF、EF即可；〔2〕根据角平分线的性质得到∠ABF =∠CBF，再根据垂直平分线的性质及角的转换得到∠CBF =∠DFB，∠ABF =∠EFB，证出四边形BEFD是平行四边形，再根据DB=DF，证出菱形。
23.【答案】 〔1〕7；30%
〔2〕解：补全条形图如下：


〔3〕140
〔4〕解：画树状图如下：

共有12种情况，选中一男一女的有6种，
那么P〔选中一男一女〕= ．
【解析】【解答】解：〔1〕本次调查的总人数为10÷25%=40〔人〕，
∴参加音乐类活动的学生人数为40×17.5%=7人，参加球类活动的人数的百分比为 ×100%=30%，
故答案为：7，30%；〔3〕该校学生共600人，那么参加棋类活动的人数约为800× =140，
故答案为：140；

【分析】〔1〕先根据绘画类人数及其百分率求出总人数，再求其它即可；〔2〕根据〔1〕中的结果作图即可；〔3〕总人数乘以棋类活动的百分比即可；〔4〕利用树状图列出所有情况，再利用概率公式求解即可。
24.【答案】 〔1〕解：如图2所示，
∵四边形ABCD是矩形
∴∠ABC =∠A = 90°
∴∠ABP＋∠PBC = 90°
∵PE⊥PF，
∴∠BPC = 90°
∴∠PCB＋∠PBC = 90°
∴∠ABP =∠PCB
∴△ABP ∽△PCB 
∴
在Rt△ABP中，
∵AB＝2，AP＝1，
∴BP＝
∴
∴PC＝2

〔2〕解：① 的值不会发生变化，理由如下：
如图3所示，

将直角从图2中的位置开始，绕点P顺时针旋转的过程中，BPC = 90°保持不变，
∴∠EPB＋∠BPF = 90°，∠CPF＋∠BPF = 90°
∴∠EPB =∠CPF
在△EBP和△FCP中，
 
∴△EBP ∽△FCP
∴   
②取EF的中点Q，连接BQ，PQ，PB，如图3．

∵∠EBF=∠EPF=90°，点Q为EF的中点，
∴QP= EF=QB，
∴点Q在线段PB的垂直平分线上；
∴点Q经过的路线是一条线段．
如图4，

当点E在点B处时，点Q在BC中点Q1处；
当点E在点A处时，点Q在PB的中点Q2处．
根据三角形中位线定理得Q1Q2= PC= ．
所以从开始到停止，线段EF的中点Q所经过的路线长Q1Q2为 ．
【解析】【分析】〔1〕先证明△ABP ∽△PCB，再根据相似三角形的性质列出比例式求解即可；〔2〕①利用旋转的性质得到角相等，证出△EBP ∽△FCP，列出比例式求解即可；②取EF的中点Q，根据直角三角形斜边上的中线等于斜边的一半可得QP=QB，从而得到点Q在线段PB的垂直平分线上，再找出点Q的终点与起点，最后利用三角形饿中位线求解即可。
25.【答案】 〔1〕解：①证明：∵AD⊥BC，
∴∠ADB＝∠CDA＝90°．
∵AD 2 ＝BD·DC，
∴ ．
∴△ABD ∽ △CAD．
∴∠BAD ＝∠C．
又∵∠B +∠BAD＝90° ，
∴∠B +∠C ＝90°．
∴∠BAC ＝ 90°．
②∵DE⊥AB，DF⊥AC，∠BAC＝90°．
∴∠EAF＝∠AED＝∠AFD＝90°．
∴四边形AEDF是矩形．
∴EF＝AD．
∵∠BAC＝90°，AD⊥BC，
∴AB2＝BD BC．
∵AB ＝4，DC ＝6，
即42＝BD 〔BD＋6〕．
解得BD＝2．
∴Rt△ABD中，AD＝ ＝ ．
∴EF＝ ；

〔2〕解：∵在Rt△ABD中，AD ＝4，BD ＝2，
∴AB＝ ．
∵AD＝4，DC＝4，DF⊥AC，
∴AC＝ ． 
∴AF＝ AC＝ ．
∵DE⊥AB，DF⊥AC，AD⊥BC，
∴AD2＝AE AB，AD2＝AF AC．
∴AE AB＝AF AC．
即 ．
又∵∠EAF＝∠CAB，
∴△AEF∽△ACB．
∴ ．
∴ ．
解得EF＝ ．
【解析】【分析】〔1〕①根据∠ADB＝∠CDA＝90°．， 可得△ABD ∽ △CAD．，再利用相似三角形的性质求解即可；②先判断四边形AEDF是矩形，得到EF=AD，利用射影定理求出BD，再利用勾股定理求解EF；〔2〕先证出△AEF∽△ACB，再列比例式求解即可。