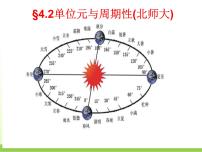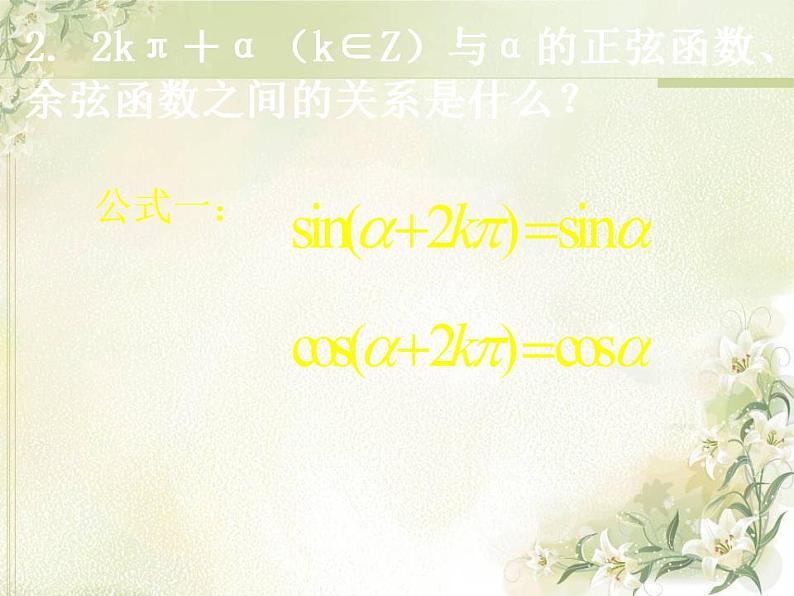
高中数学北师大版必修44.3单位圆与诱导公式课堂教学ppt课件

这是一份高中数学北师大版必修44.3单位圆与诱导公式课堂教学ppt课件，共26页。PPT课件主要包含了公式二等内容，欢迎下载使用。

一、教学目标 1、会利用单位圆研究正弦、余弦函数的诱导公式。2、在利用单位圆的对称性推导诱导公式中，进一步培养几何方法研究代数问题的意识。3、观察正弦、余弦函数值的变化规律，再次体会对称性在研究问题中的价值。
教学重点难点：教学重点：正弦函数、余弦函数诱导公式的推导教学难点：正弦函数、余弦函数诱导公式的推导
1.单位圆中任意角α的正弦、余弦是怎样定义的？
2. 2kπ＋α（k∈Z）与α的正弦函数、余弦函数之间的关系是什么？
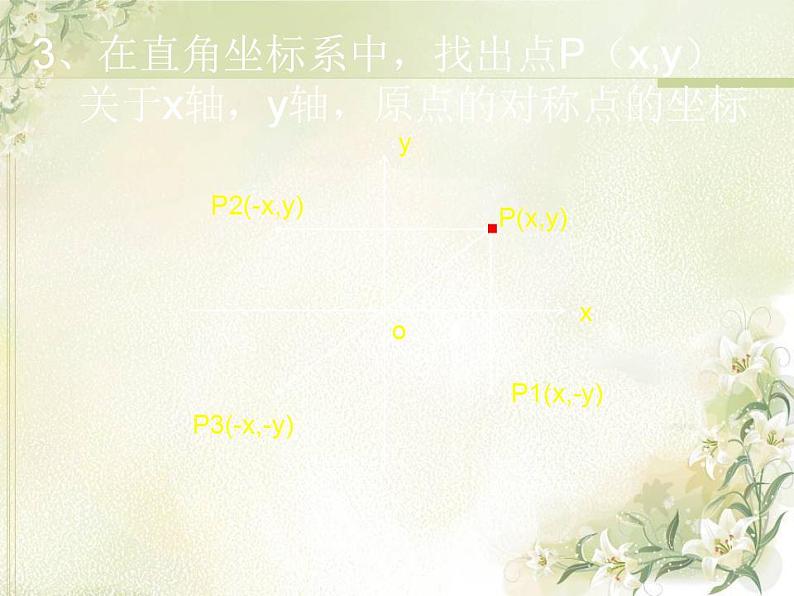
3、在直角坐标系中，找出点P（x,y） 关于x轴，y轴，原点的对称点的坐标
4.利用公式一，可将任意角的三角函数值，转化为00～3600范围内的三角函数值.其中锐角的三角函数可以查表计算，而对于900～3600范围内的三角函数值，如何转化为锐角的三角函数值，是我们需要研究和解决的问题.
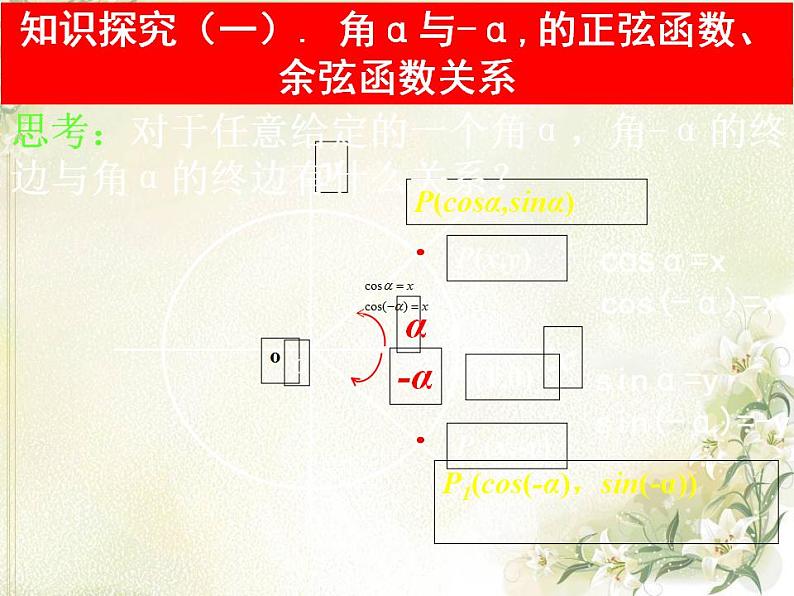
知识探究（一）. 角α与-α,的正弦函数、余弦函数关系
P(csα,sinα)
P1(cs(-α)，sin(-α))
思考：对于任意给定的一个角α，角-α的终边与角α的终边有什么关系？
csα=xcs(-α)=x
sinα=ysin(-α)=-y
sin(-α) = -sinα cs(-α) = csα
思考：对于任意给定的一个角α，角α＋π、α-π的终边与角α的终边有什么关系？
知识探究（二）：角α与α±π的正.余弦函数关系
思考：设角α的终边与单位圆交于点P（x，y），则角α＋π、α-π的终边与单位圆的交点坐标如何？
思考：根据正弦函数、余弦的函数定义，sin（α＋π） 、cs（α＋π）、sin（α-π） 、cs（α-π）、的值分别是什么？
sin(α＋π)=-y
sin(α-π)=-y
思考：对比sinα，csα的值，π＋α的正弦、余弦函数与α的正弦、余弦函数有什么关系？
sin(α+π) = -sinα cs(α+π) = -csα
sin(α-π) = -sinα cs(α-π) = -csα
知识探究（三）：角α与π-α的正弦、余弦函数关系
P1(cs(π-α)，sin(π-α))
思考：对于任意给定的一个角α，π-α的终边与α的终边有什么关系？
sin(π-α) = sinα cs(π-α) = -csα
例1 求下列各三角函数的值：
求值步骤：负化正，大化小，化成锐角再求值
练习2：（1）已知csx＝ ，求cs(π+x)的值.
（2）已知cs(π+x)= ，求cs(π－x)的值.
1.利用圆的对称性及角终边的对称性探索诱导公式的方法
3.利用诱导公式一～四，可以求任意角的正弦、余弦函数，其基本思路是：
这是一种化归与转化的数学思想.
布置作业： P20练习：1，2.写在书本上 P24：8.（2）写在作业本上