高中数学高教版（中职）拓展模块3.3.1 离散型随机变量课前预习课件ppt

这是一份高中数学高教版（中职）拓展模块3.3.1 离散型随机变量课前预习课件ppt，共25页。PPT课件主要包含了复习引入，新课引入，离散型随机变量，练一练，数学应用，概率分布列等内容，欢迎下载使用。

定义3：在一定条件下可能发生也可能不发生 的事件叫随机事件。
定义1：在一定条件下必然要发生的事件叫 必然事件。
定义2：在一定条件下不可能发生的事件叫 不可能事件。
按事件结果发生与否来进行分类 :
①求一个事件概率的基本方法是通过大量的重复试验。
事件A的概率： 一般地，在大量重复进行同一试验时，事件A发生的频率 m/n 总是接近于某个常数，在它附近摆动。这个常数叫做事件 A 的概率，记作 P(A)。
②当频率在某个常数附近摆动时，这个常数叫做事件A的概率。
③概率是频率的稳定值，而频率是概率的近似值。
④概率反映了随机事件发生的可能性的大小。
⑤随机事件A在n次试验中发生m次，则0≤m ≤n 因此 0≤P（A）≤1 。
⑥必然事件的概率是1，不可能事件的概率是0
1、什么是随机事件？什么是基本事件？
在一定条件下可能发生也可能不发生的事件，叫做随机事件。试验的每一个可能的结果称为基本事件。
问题1:某人射击一次,可能出现:
问题2:某次产品检查,在可能含有次品的 100 件产品中，任意抽取 4 件，
那么其中含有次品可能是: 0件，1件，2件，3件，4件.
即,可能出现的结果可以由: 0, 1, 2, 3, 4 表示.
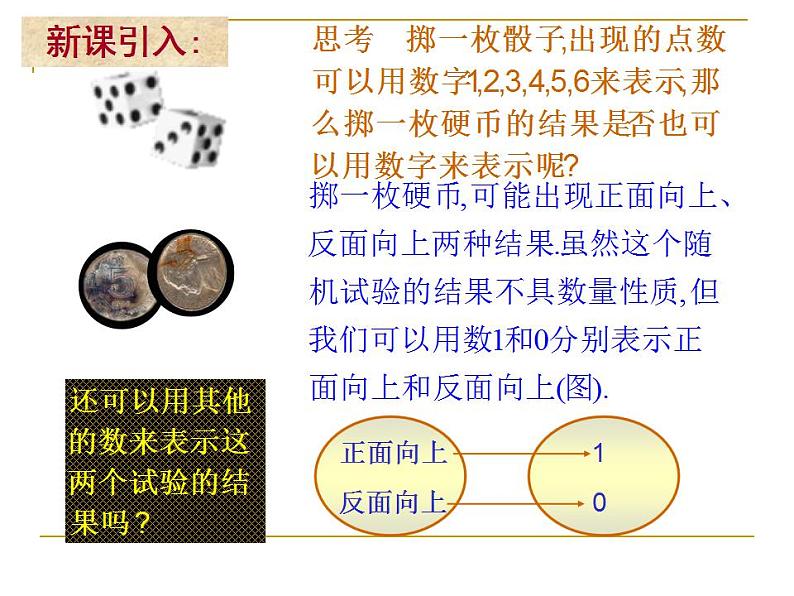
如果随机试验的结果可以用一个变量来表示，（或随着试验结果变化而变化的变量），那么这样的变量叫做随机变量．
②每次试验总是恰好出现这些结果中的一个，但在一次试验之前却不能肯定这次试验会出现哪一个结果．
①试验的所有可能结果可以用一个数来表示；
在上面例子中，随机试验有下列特点:
随机变量常用希腊字母X、Y、ξ、η等表示。
1. 随机变量
在问题1中:某人射击一次,命中的环数为ξ.
ξ=0,表示命中 0 环
ξ=1,表示命中 1 环
ξ=10,表示命中 10 环;
在问题2中:产品检查任意抽取 4件, 含有的次品数为η;
η=0,表示含有 0 个次品;
η=1,表示含有 1 个次品;
η=2,表示含有 2 个次品;
η=4,表示含有 4 个次品;
问题：1、对于上述试验，可以定义不同的随机变量来表示这个试验结果吗？2、在掷骰子试验中，如果我们仅关心掷出的点数是否为偶数，应如何定义随机变量？
3、任何随机试验的所有结果都可以用数字表示吗？
本质是建立了一个从试验结果到实数的对应关系。
在上面的射击、产品检验等例子中，对于随机变量可能取的值，我们可以按一定次序一一列出，
这样的随机变量叫做离散型随机变量．
所有取值可以一一列出的随机变量，称为离散型随机变量。
如果随机变量可能取的值是某个区间的一切值，这样的随机变量叫做连续型随机变量.
某林场树木最高达30m,那么这个林场的树木高度的情况有哪些?
(0，30]内的一切值
写出下列各随机变量可能的取值.
（1）从10张已编号的卡片（从1号到10号）中任取1张，被取出的卡片的号数 ．
（2）一个袋中装有5个白球和5个黑球，从中任取3个，其中所含白球数 ．
（3）抛掷两个骰子，所得点数之和　．
（4）接连不断地射击，首次命中目标需要的射击次数 ．　
（5）某一自动装置无故障运转的时间　．
（6）某林场树木最高达50米，此林场树木的高度　．
（7）新生婴儿的性别，抽查的结果可能是男，也可能是女，如果用0表示男婴，用1表示女婴，那么抽查的结果Z是0与1中的某个数.
Ｚ＝０，表示新生婴儿是男婴；
Ｚ＝１，表示新生婴儿是女婴．
例1（1）掷一枚质地均匀的硬币一次，用X表示掷得正面的次数，则随机变量X的可能取值有哪些？
随机事件“掷一枚硬币，反面向上”可用随机变量简单表示为{X=0}。其概率为:P({X=0})=P{掷一枚硬币，反面向上}=0.5简记为P(X=0)=0.5{X=1}的概率可以表示为:P({X=1})=P{掷一枚硬币，正面向上}=0.5简记为P(X=1)=0.5故随机变量X的取值构成集合{0，1}
（2）一实验箱中装有标号为1，2，3，3，4的五只白鼠，从中任取一只，记取到白鼠的标号为Y，则随机变量Y的可能取值有哪些？
解：随机变量Y可能值有4种，它的取值集合为{1，2，3，4}
例1的结果用表格描述：
一般地，假定随机变量X有n个不同的取值，它们分别是x1,x2, …,xn且P(X=xi)=pi, （i=1,2, …,n）则称为随机变量X 的分布列，简称为X的分布列.
此表叫概率分布表，它和分布列都叫做概率分布。
可以一一列出，也可写出通项
（1）Pi≥0(i=1,2,…,n)（2）P1+p2+ …+pn=1
例2: 从装有6只白球和4 只红球的口袋中任取一只白球，用X表示“取到的白球个数”，即
求随机变量X的概率分布.
P（X=0）=P（X=1）=
解:根据分布列的性质,针尖向下的概率是(1—p)，于是，随机变量X的分布列是：
像上面这样的分布列称为两点分布列。如果随机变量X的分布列为两点分布列，就称X服从两点分布，而称p=P(X=1)为成功概率。
P(0P（X=1）+P（X=2）
=1/2+1/6=2/3
=P(抽得的两件全为次品)
2 设有一批产品20件，其中有3件次品，从中任意抽取2件，如果用X表示取得的次品数，求随机变量X的分布律及事件“至少抽得一件次品”的概率。
解：X的可能取值为 0，1，2
=P(抽得的两件全为正品)
=P(只有一件为次品)
而“至少抽得一件次品”={X≥1}
= {X=1}{X=2}
P{X≥1}= P{X=1}+P{X=2}
注意：{X=1}与{X=2}是互不相容的！
3.随机变量ξ的分布列为
解:(1)由离散型随机变量的分布列的性质有
（1）求常数a;（2）求P(1<ξ<4)
(2)P(1<ξ<4)=P(ξ=2)+P(ξ=3)=0.12+0.3=0.42
4、下列A、B、C、D四个表，其中能成为随机变量 的分布列的是（ ）