






高中数学沪教版高中三年级 第一学期16.2排列授课ppt课件
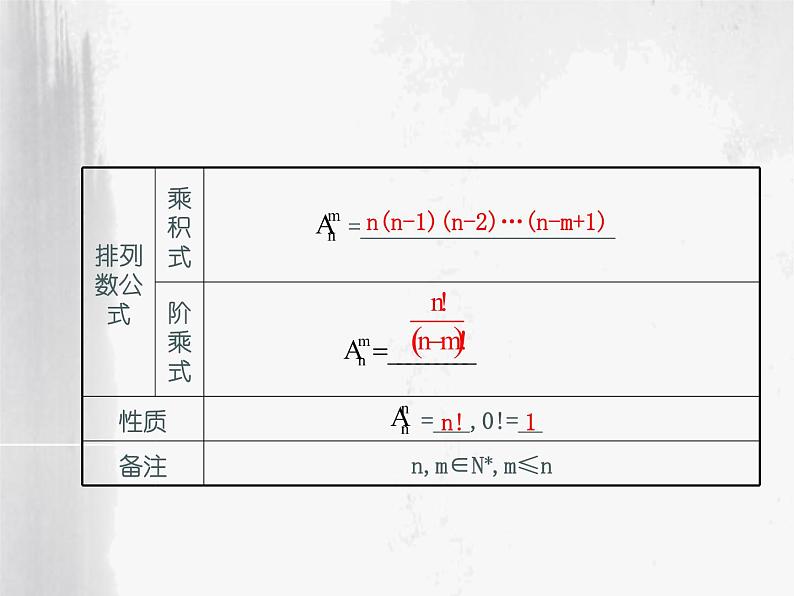
展开n(n-1)(n-2)…(n-m+1)
判断:(正确的打“√”,错误的打“×”)(1)对于式子 中的x可以取小于或等于3的任意整数.( )(2)排列数 是有n个因式的乘积.( )(3)0!规定等于1,但它不能按阶乘的含义来解释.( )(4) (n∈N*且n<55)( )
提示:(1)错误.x≤3且x∈N*.(2)错误.从n-m+1到n共有m个因式相乘.(3)正确.0!=1只是一种规定.(4)错误.(55-n)(56-n)…(69-n)共有15个因式相乘,故原式等于 (n∈N*且n≤54).答案:(1)× (2)× (3)√ (4)×
【知识点拨】1.排列与排列数的区别“排列”和“排列数”是两个不同的概念,一个排列是指“从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列”,它不是一个数,而是具体的一个排列(也就是具体的一件事);排列数是指“从n个不同的元素中取出m(m≤n)个元素的所有排列的个数”,它是一个数.
比如从3个元素a,b,c中取出2个元素,按照一定的顺序排成一列,有如下几种:ab,ac,ba,bc,ca,cb,每一种都是一个排列,共有6种,而数字6就是排列数,符号 表示排列数,在此例中
2.准确理解排列数公式(1)公式中的n,m应该满足n,m∈N*,m≤n,当m>n时不成立.(2)排列数有两个公式,第一个公式右边是若干数的连乘积,其特点是:第一个因数是n(下标),后面的每一个因数都比它前面的因数少1,最后一个因数为n-m+1(下标-上标+1),共有m(上标)个连续自然数相乘.
(3)排列数的第二个公式是阶乘的形式,所以又叫排列数的阶乘式.它是一个分式的形式,分子是下标n的阶乘,分母是下标减上标的阶乘,即(n-m)的阶乘.(4)特别地,规定0!=1.这只是一种规定,不能按阶乘的含义作解释.
类型一 排列数的计算问题 【典型例题】1.(2013·洛阳高二检测)乘积m(m+1)(m+2)(m+3)…(m+20)可表示为( )2.计算:
【解题探究】1.排列数 是几个因式的乘积?最大、最小数分别是什么?2.题2(2)中 能否均用 表示?探究提示:1.从n-m+1到n共有m个因式相乘,其中最小数为n-m+1,最大数为n.2.能.
【解析】1.选D.因为m,m+1,m+2,…,m+20中最大的数为m+20,且共有m+20-m+1=21个因式. 所以m(m+1)·(m+2)…(m+20)=
2.(1)(2)方法一:
【互动探究】在题1中,若将乘积改为m(m-1)(m-2)(m-3)…(m-20)(m>20),则结果如何?【解析】因为m(m-1)(m-2)…(m-20)中最大数为m,且共有m-(m-20)+1=21(个)因式,所以m(m-1)(m-2)…(m-20)=
【拓展提升】排列数的计算方法(1)排列数的计算主要是利用排列数的乘积公式进行,应用时注意:连续正整数的积可以写成某个排列数,其中最大的是排列元素的总个数,而正整数(因式)的个数是选取元素的个数,这是排列数公式的逆用.
(2)应用排列数公式的阶乘形式时,一般写出它们的式子后,再提取公因式,然后计算,这样往往会减少运算量.(3)当计算的式子中含有多个排列数时,一般先利用阶乘的性质将其他排列数用最小的排列数表示,再计算.
类型二 与排列数有关的方程、不等式及证明问题【典型例题】 1.(1)已知 则n=______.(2)不等式 的解集为______.2.求证:
【解题探究】1.如何利用排列数公式将题1(1)(2)中的方程、不等式转化为n或x的代数方程、不等式求解?2.如何选择排列数公式由题2中待证式左端过渡到右端?探究提示:1.利用排列数公式的乘积式或阶乘式进行转化.2.对 分别用排列数公式的阶乘形式过渡到右端.
【解析】1.(1)因为 所以2n(2n-1)(2n-2)=10n(n-1)(n-2),即n2-9n+8=0,解得n=1或n=8,因为n≥3,所以n=8.答案:8
(2)由 得3≤x≤8,x∈N*.由 得化简得x2-19x+84<0,解得7
2.排列数的化简与证明技巧应用排列数公式可以对含有排列数的式子进行化简和证明,化简的过程中要对排列数进行变形,并要熟悉排列数之间的内在联系.解题时要灵活地运用如下变式:①n!=n(n-1)!;②③n·n!=(n+1)!-n!;④
【变式训练】1.解方程:【解题指南】首先明确x≥3且x∈N*,由排列数公式列出方程,解方程即可.
【解析】由已知得所以x≥3,x∈N*.又由 得(2x+1)·2x·(2x-1)(2x-2)=140x(x-1)(x-2),化简得,4x2-35x+69=0,解得 (舍),所以方程的解为x=3.
类型三 利用排列与排列数解简单计数应用题 【典型例题】1.从1,2,…,8中任取3个数组成无重复数字的三位数,共有______个.2.(2013·兰州高二检测)一条铁路原有n个车站,为了适应客运需要,新增加了m(m>1)个车站,客运车票增加了62种,问原有多少个车站?现有多少个车站?
【解题探究】1.每一个三位数对应怎样的一个排列?所求三位数的个数是怎样的一个排列数?2.每一种车票对应怎样的一个排列?探究提示:1.每一个三位数对应从8个不同元素任取3个元素的一个排列,故所求三位数的个数为2.每一种车票对应从n个或(n+m)个不同元素,任取2个元素的一个排列.
【解析】1.按顺序,有百位、十位、个位3个位置,8个数字中取出3个依次排列,有 个.答案:336
2.因为原有车站n个,所以原有客运车票有 种,又现有(n+m)个车站,现有客运车票 种.所以 所以(n+m)(n+m-1)-n(n-1)=62,所以 所以 即62>m2-m.所以m2-m-62<0.又m>1,从而得出 所以1
2.解简单的排列应用题的思路(1)认真分析题意,看能否把问题归结为排列问题,即是否有顺序.(2)如果是的话,再进一步分析,这里n个不同的元素指的是什么,以及从n个不同的元素中任取m(m≤n)个元素的每一种排列对应的是什么事件.(3)运用排列数公式求解.
【变式训练】有5个不同的科研小课题,从中选3个由高二(4)班的3个学习兴趣小组进行研究,每组一个课题,共有多少种不同的安排方法?【解析】从5个不同的课题中选3个,由3个兴趣小组进行研究,每种选法对应于从5个不同元素中选出3个元素的一个排列.因此不同的安排方法有 (种).
【易错误区】忽视排列数中的隐含条件致误【典例】已知 则n为( )A.7,8,9,10,11,12 B.8,9 C.7,8 D.7
【解析】选C.由排列数公式得,所以即所以
化简为n2-19n+78<0,所以6
【类题试解】不等式 的解集为______.【解析】由题意可得所以解得n=3或n=4,所以原不等式的解集是{3,4}.答案:{3,4}
1.乘积5×6×7×…×20等于( )【解析】选B.根据题意,由于乘积5×6×7×…×20表示的是从20到5的连续16个自然数的乘积,则可知表示的为
2.从5本不同的书中选出2本送给2名同学,每人一本,共有多少种给法( )A.5种 B.10种 C.20 种 D.60 种【解析】选C.由排列数定义知,共有 (种).
3.若 则x=( )【解析】选B.因为所以
4.满足 的n的解集为______.【解析】由 得 且n∈N*,所以n的解集为{n|n>4且n∈N*}.答案:{n|n>4且n∈N*}
5.方程 的解x=______.【解析】 =(x-3)(x-4)+(x-3)=x2-6x+9=4,所以x2-6x+5=0,解得x=5或x=1(舍).答案:5
高中16.2排列图文课件ppt: 这是一份高中16.2排列图文课件ppt,共16页。PPT课件主要包含了基本概念,课堂练习等内容,欢迎下载使用。
高中数学沪教版高中三年级 第一学期16.2排列示范课课件ppt: 这是一份高中数学沪教版高中三年级 第一学期16.2排列示范课课件ppt,共7页。
高中数学沪教版高中三年级 第一学期16.2排列图文课件ppt: 这是一份高中数学沪教版高中三年级 第一学期16.2排列图文课件ppt,共44页。PPT课件主要包含了一定的顺序,相同排列,画出下列树形图,误区警示,列举如下等内容,欢迎下载使用。













