

2020-2021学年河南省南阳市高三(下)5月月考数学(理)试卷 (1)北师大版
展开1. 已知集合A=x|x2−2x≤0,B=x|1
2. 设复数z满足z2+i=2−i,则z在复平面内对应的点位于( )
A.第一象限B.第二象限C.第三象限D.第四象限
3. 在△ABC中,BC=17,AC=3,csA=13,则△ABC的面积为( )
A.42B.2C.4D.92
4. 生物入侵指生物由原生存地侵入到另一个新的环境,从而对入侵地的生态系统造成危害的现象.若某入侵物种的个体平均繁殖数量为Q,一年四季均可繁殖,繁殖间隔T为相邻两代间繁殖所需的平均时间.在物种入侵初期,可用对数模型Kn=λlnn来描述该物种累计繁殖数量n与入侵时间K(单位:天)之间的对应关系,且Q=Tλ+1,在物种入侵初期,基于现有数据得出Q=9,T=80.据此,累计繁殖数量比现有数据增加3倍所需要的时间约为( )
(ln2≈0.69,ln3≈1.10)
A.6.9天B.11.0天C.13.8天D.22.0天
5. 某几何体的三视图如图所示,则该几何体最长棱与最短棱所在直线夹角的余弦值为( )
A.8210B.225C.210D.3210
6. 家庭开支是指一般生活开支的人均细分.如图所示的是2017年和2020年小王的家庭收入用于各项支出的比例分配图,其中房贷每年的还款数额相同.根据以上信息,判断下列结论中正确的是( )
A.小王一家2020年的家庭收入比2017年增加了1倍
B.小王一家2020年用于其他方面的支出费用是2017年的2倍
C.小王一家2020年用于饮食的支出费用相比2017年明显增加
D.小王一家2020年用于娱乐的费用比2017年增加了7%
7. 已知非零向量a→,b→满足|b→|=2|a→|,且a→−b→⊥3a→+2b→,则a→与b→的夹角为( )
A.45∘B.135∘C.60∘D.120∘
8. 三星堆遗址,位于四川省广汉市,距今约三千到五千年.2021年2月4日,在三星堆遗址祭祀坑区4号坑发现了玉琮.玉琮是一种内圆外方的筒型玉器,是一种古人用于祭祀的礼器.假定某玉琮中间内空,形状对称,如图所示,圆筒内径长2cm,外径长3cm,筒高4cm,中部为棱长是3cm的正方体的一部分,圆筒的外侧面内切于正方体的侧面,则该玉琮的体积为( )
A.27−7π4cm3B.24+π4cm3C.36−9π4cm3D.18+7π4cm3
9. 把函数y=2sin2x的图象向左平移π3个单位长度,再将所得图象向上平移1个单位长度,可得到函数fx的图象,则( )
A.fx=2sin2x+π3+1B.fx的最小正周期为2π
C.fx的图象关于直线x=π6对称D.fx在π6,5π12上单调递减
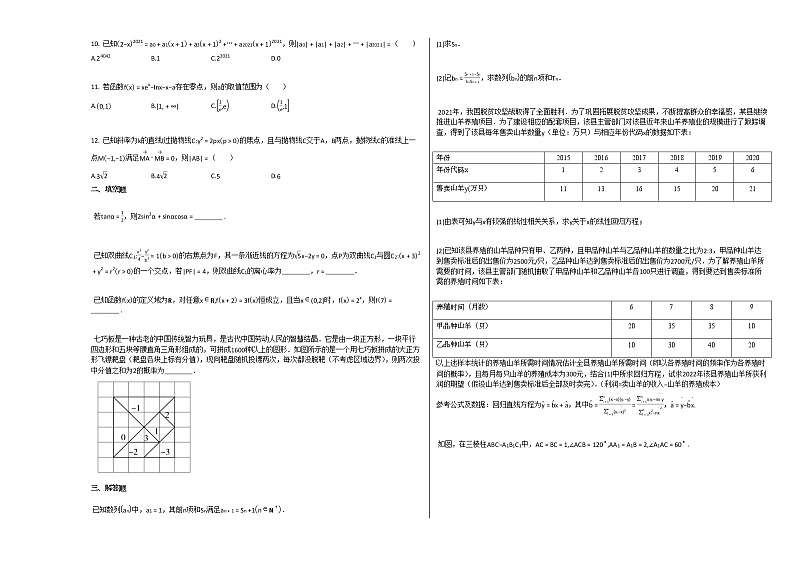
10. 已知2−x2021=a0+a1x+1+a2x+12+⋯+a2021x+12021,则|a0|+|a1|+|a2|+⋯+|a2021|=( )
A.24042B.1C.22021D.0
11. 若函数fx=xex−lnx−x−a存在零点,则a的取值范围为( )
A.0,1B.[1,+∞)C.1e,eD.1e,1
12. 已知斜率为k的直线l过抛物线C:y2=2pxp>0的焦点,且与抛物线C交于A,B两点,抛物线C的准线上一点M−1,−1满足MA→⋅MB→=0,则|AB|=( )
A.32B.42C.5D.6
二、填空题
若tanα=12,则2sin2α+sinαcsα=________ .
已知双曲线C1:x24−y2b2=1b>0的右焦点为F,其一条渐近线的方程为5x−2y=0,点P为双曲线C1与圆C2:x+32+y2=r2r>0的一个交点,若|PF|=4,则双曲线C1的离心率为________,r=________.
已知函数fx的定义域为R,对任意x∈R,fx+2=3fx恒成立,且当x∈(0,2]时,fx=2x,则f7=________ .
七巧板是一种古老的中国传统智力玩具,是古代中国劳动人民的智慧结晶.它是由一块正方形,一块平行四边形和五块等腰直角三角形组成的,可拼成1600种以上的图形.如图所示的是一个用七巧板拼成的大正方形飞镖靶盘(靶盘各块上标有分值),现向靶盘随机投镖两次,每次都没脱靶(不考虑区域边界),则两次投中分值之和为2的概率为________.
三、解答题
已知数列an中,a1=1,其前n项和Sn满足an+1=Sn+1n∈N∗.
(1)求Sn.
(2)记bn=Sn+1−SnSnSn+1,求数列bn的前n项和Tn.
2021年,我国脱贫攻坚战取得了全面胜利.为了巩固拓展脱贫攻坚成果,不断提高群众的幸福感,某县继续推进山羊养殖项目.为了建设相应的配套项目,该县主管部门对该县近年来山羊养殖业的规模进行了跟踪调查,得到了该县每年售卖山羊数量y(单位:万只)与相应年份代码x的数据如下表:
(1)由表可知y与x有较强的线性相关关系,求y关于x的线性回归方程;
(2)已知该县养殖的山羊品种只有甲、乙两种,且甲品种山羊与乙品种山羊的数量之比为2:3,甲品种山羊达到售卖标准后的出售价为2500元/只,乙品种山羊达到售卖标准后的出售价为2700元/只.为了解养殖山羊所需要的时间,该县主管部门随机抽取了甲品种山羊和乙品种山羊各100只进行调查,得到要达到售卖标准所需的养殖时间如下表:
以上述样本统计的养殖山羊所需时间情况估计全县养殖山羊所需时间(即以各养殖时间的频率作为各养殖时间的概率),且每月每只山羊的养殖成本为300元,结合(1)中所求回归方程,试求2022年该县养殖山羊所获利润的期望(假设山羊达到售卖标准后全部及时卖完).(利润=卖山羊的收入−山羊的养殖成本)
参考公式及数据:回归直线方程为y=bx+a,其中b=i=1n(xi−x¯)(yi−y¯)i=1n(xi−x¯)2=i=1nxiyi−nx¯ y¯i=1nxi2−nx¯2,a=y¯−bx¯.
如图,在三棱柱ABC−A1B1C1中,AC=BC=1,∠ACB=120∘,AA1=A1B=2,∠A1AC=60∘ .
(1)证明:平面ABC⊥平面A1ACC1;
(2)若CP→=13CC1→,求二面角P−A1B−A的余弦值.
已知椭圆E:x2a2+y2b2=1a>b>0的离心率为12,椭圆上的点离右焦点F的最短距离为1.
(1)求椭圆E的方程;
(2)直线l(斜率不为0)经过F点,与椭圆E交于A,B两点,问x轴上是否存在一定点P,使得|PA||PB|=|AF||BF|?若存在,求出P点的坐标;若不存在,请说明理由.
已知函数fx=2alnx−x+12x2.
(1)若a=12,求曲线y=fx在点(1,f(1))处的切线方程;
(2)若fx的两个极值点为x1,x2,且x2>e2x1,不等式fx1−fx2>bx12−x22恒成立,求实数b的取值范围.
在直角坐标系xOy中,直线l的参数方程为x=1−t,y=−1+2t(t为参数),以原点O为极点,x轴非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2=12sin2θ+3 .
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)已知点P1,−1,直线l与曲线C交于A,B两点,求1|PA|+1|PB| .
已知函数fx=|x−2t|−|x+t|t>0.
(1)当t=1时,求不等式fx≥1的解集;
(2)若t2≥fx对任意的x∈R恒成立,M=t+t+8t−1,求M的最小值.
参考答案与试题解析
2020-2021学年河南省南阳市高三(下)5月月考数学(理)试卷
一、选择题
1.
【答案】
B
【考点】
一元二次不等式的解法
并集及其运算
【解析】
本题考查集合的并集.
【解答】
解:因为A={x|0≤x≤2},B={x|1
故选B.
2.
【答案】
D
【考点】
复数的代数表示法及其几何意义
复数代数形式的乘除运算
【解析】
无
【解答】
解:因为z=2−i2+i=3−4i5=35−45i,
所以z在复平面内对应的点位于第四象限.
故选D.
3.
【答案】
A
【考点】
同角三角函数间的基本关系
余弦定理
三角形的面积公式
【解析】
本题考查余弦定理,考查运算求解能力.
【解答】
解:∵BC=17,AC=3,csA=13,
由余弦定理得BC2=AB2+AC2−2AB⋅ACcsA,
∴AB2−2AB−8=0,
∴AB=4,
又∵csA=13,
∴sinA=223,
∴ S△ABC=12AB⋅AC⋅sinA=12×4×3×223=42.
故选A.
4.
【答案】
C
【考点】
函数的求值
【解析】
本题考查函数的性质,考查信息提取能力及运算求解能力.
【解答】
解:∵Q=Tλ+1,Q=9,T=80.
∴9=80λ+1.
解得λ=10.
设初始时间为K1.
初始累计繁殖数量为n,累计繁殖数量增加3倍后的时间为K2.
则K2−K1=λln4n−λlnn=λln4=20ln2≈13.8天.
故选C.
5.
【答案】
D
【考点】
简单空间图形的三视图
两直线的夹角
【解析】
本题考查三视图,考查空间想象能力与运算求解能力.
【解答】
解:该几何体是三棱锥,将该三棱锥放入长方体中.
如图,由三视图可知长方体的长、宽,高分别为3,4,5.
计算可得最长棱PB=52,最短棱AB=3.
因为AB⊥PA,
所以最长棱与最短棱所在直线夹角的余弦值为3210.
故选D .
6.
【答案】
C
【考点】
扇形统计图
【解析】
无
【解答】
解:A,因为小王家房贷每年的还款数额相同,
设为a,则2017年总收入为53a,2020年总收入为52a.
因此小王家2020年的家庭收入比2017年增加56a,
即增加了50%,所以A错误.
B,因为小王家2017年和2020年用于其他方面的支出费用分别为110a和310a,所以B错误.
C,因为小王家2017年和2020年用于饮食的费用分别为512a,58a,明显增加,所以C正确.
D,因为小王家2017年和2020年的总收入不一样,所以D错误.
故选C.
7.
【答案】
B
【考点】
平面向量数量积的运算
数量积表示两个向量的夹角
数量积判断两个平面向量的垂直关系
【解析】
本题考查平面向量的数量积,考查运算求解能力 .
【解答】
解:∵ |b→|=2|a→|,a→−b→⊥3a→+2b→,
∴ a→−b→⋅3a→+2b→=3a→2−a→⋅b→−2b→2
=−a→2−a→⋅b→=0,
∴ a→2=−a→⋅b→,
设a→与b→的夹角为θ,
csθ=a→⋅b→|a→|⋅|b→|=−22.
∵ θ∈[0∘,180∘],
∴ θ=135∘.
故选B.
8.
【答案】
A
【考点】
组合几何体的面积、体积问题
【解析】
此题暂无解析
【解答】
解:由图可知,组合体的体积为V=π×4×[(32)2−12]+3×3×3−π×3×(32)2=27−7π4cm3.
故选A.
9.
【答案】
D
【考点】
函数y=Asin(ωx+φ)的图象变换
正弦函数的图象
正弦函数的单调性
【解析】
本题考查三角函数的图象及其性质,考查运算求解能力.
【解答】
解:将其图象向左平移π3个单位长度得到y=2sin[2x+π3]=2sin2x+2π3的图象,
再向上平移1个单位长度可得到fx=2sin2x+2π3+1的图象,故A、B错误.
令2x+2π3=π2+kπ,k∈Z,
得x=−π12+kπ2,
当k=0时,x=−π12,
当k=1时,x=5π12,故C错误.
令π2+2kπ≤2x+2π3≤3π2+2kπ,k∈Z,
得−π12+kπ≤x≤5π12+kπ,k∈Z,
∴fx在[π6,5π12]上单调递减,故D正确.
故选D.
10.
【答案】
A
【考点】
二项式系数的性质
二项展开式的特定项与特定系数
【解析】
本题考查二项式定理,考查运算求解能力.
【解答】
解:因为2−x2012=3−x+12012的展开式中,a0,a2,a4,⋯,a2020都大于零,
而a1,a3,a5,⋯,a2021都小于零,
所以|a0|+|a1|+|a2|+⋯+|a2021|=a0+a2+a4⋯+a2020−a1+a3+a5+⋯+a2021.
令x=−2,则a0−a1+a2−a3+a4−a5+⋯+a2020−a2021=42021.
所以|a0|+|a1|+|a2|+⋯+|a2012|=24042.
故选A.
11.
【答案】
B
【考点】
利用导数研究与函数零点有关的问题
【解析】
本题考查导数在函数中的应用.
【解答】
解:f′(x)=ex+xex−1x−1=(x+1)ex−1x,
因为x>0,
所以x+1>0.
令g(x)=ex−1x,
因为g(x)在(0,+∞)上单调递增,
所以∃x0∈(0,+∞),g(x0)=0,即x0+lnx0=0.
当x∈(0,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0.
所以f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,
所以f(x)min=f(x0)=x0ex0−lnx0−x0−a=1−a.
要使f(x)存在零点,只需f(x)min≤0,即a≥1.
故选B.
12.
【答案】
C
【考点】
抛物线的性质
抛物线的标准方程
圆锥曲线的综合问题
【解析】
本题考查抛物线的性质,考查化归与转化的数学思想及运算求解能力.
【解答】
解:由题意知,抛物线C的准线为x=−1,即p2=1,得p=2,
所以抛物线C的方程为y2=4x,其焦点为F(1,0),
因为直线l过抛物线的焦点F1,0,所以直线l的方程为y=kx−1 .
因为MA→⋅ MB→=0,
所以M在以AB为直径的圆上.
设点Ax1,y1,Bx2,y2,
联立方程组y12=4x1,y22=4x2,
两式相减可得y1−y2x1−x2=4y1+y2=k .
设AB的中点为Qx0,y0,
则y0=2k,
因为点Qx0,y0在直线l上.
所以x0=2k2+1.
所以点Q2k2+1,2k是以AB为直径的圆的圆心.
由抛物线的定义知,圆Q的半径r=AB2=x1+x2+22=2x0+22=2k2+2,
因为|QM|2=2k2+22+2k+12=r2,
所以(2k2+2)2+(2k+1)2=2k2+22,
解得k=−2,
所以弦长|AB|=2r=22k2+2=224+2=5 .
故选C .
二、填空题
【答案】
45
【考点】
同角三角函数基本关系的运用
三角函数的恒等变换及化简求值
【解析】
本题考查三角恒等变换,考查运算求解能力.
【解答】
解:∵tanα=12,
∴2sin2α+sinαcsα=2sin2α+sinαcsαsin2α+cs2α=2tan2α+tanαtan2α+1=45.
故答案为:45.
【答案】
32,8
【考点】
双曲线的渐近线
双曲线的标准方程
双曲线的离心率
圆锥曲线的综合问题
【解析】
本题考查双曲线的离心率及圆的方程,老查化归与转化的数学思想.
【解答】
解:设F2为双曲线C1:x24−y2b=1的左焦点,
因为a=2,—条渐近线的方程为5x−2y=0,
所以b=5,
故离心率1+ba2=32.
圆C2的圆心为双曲线C1的左焦点,连接PF2,
因为|PF|=4.
所以P在双曲线的右支上,
由|PF2|− |PF|=2a=4,
得r=|PF2|=8 .
故答案为:32;8.
【答案】
54
【考点】
抽象函数及其应用
函数的求值
函数的周期性
【解析】
本题考查函数的性质,考查运算求解能力.
【解答】
解:∵fx+2=3fx,
∴f7=3f5=32f(3)=33f(1)=54 .
故答案为:54.
【答案】
564
【考点】
几何概型计算(与长度、角度、面积、体积有关的几何概型)
【解析】
本题考查相互独立事件的概率,考查逻辑推理与数学运算的核心素养 .
【解答】
解:由图可知,P(−1)=14,P(−2)=18,
P(−3)=18,P(0)=14,
P(1)=18,P(2)=116,P(3)=116,
所以两次投中分值之和为2的概率为116×14×2+116×14×2+18×18=564 .
故答案为:564.
三、解答题
【答案】
解:(1)当n≥2时,an=Sn−1+1 ,
∴an+1−an=Sn−Sn−1=an,
即an+1=2ann≥2 ,
在an+1=Sn+1中,
令n=1,
可得a2=a1+1,
∵a1=1,
∴a2=2a1 ,
故{an}是首项为1,公比为2的等比数列,
其通项公式为an=2n−1 ,
∴Sn=an+1−1=2n−1.
(2)∵bn=Sn+1−SnSnSn+1=1Sn−1Sn+1=12n−1−12n+1−1 ,
∴Tn=(1−13)+(13−17)+⋯+(12n−1−12n+1−1)=1−12n+1−1.
【考点】
数列递推式
等比数列的通项公式
数列的求和
【解析】
无
无
【解答】
解:(1)当n≥2时,an=Sn−1+1 ,
∴an+1−an=Sn−Sn−1=an,
即an+1=2ann≥2 ,
在an+1=Sn+1中,
令n=1,
可得a2=a1+1,
∵a1=1,
∴a2=2a1 ,
故{an}是首项为1,公比为2的等比数列,
其通项公式为an=2n−1 ,
∴Sn=an+1−1=2n−1.
(2)∵bn=Sn+1−SnSnSn+1=1Sn−1Sn+1=12n−1−12n+1−1 ,
∴Tn=(1−13)+(13−17)+⋯+(12n−1−12n+1−1)=1−12n+1−1.
【答案】
解:(1)∵x¯=1+2+3+4+5+66=3.5,
y¯=11+13+16+15+20+216=16 ,
∴b=−2.5×(−5)+(−1.5)×(−3)+(−0.5)×0+0.5×(−1)+1.5×4+2.5×5(−2.5)2+(−1.5)2+(−0.5)2+0.52+1.52+2.52
=3517.5=2,
可得a=16−2×3.5=9 ,
∴y与x之间的线性回归方程为y=2x+9.
(2)由(1)可知,当x=8时,可得y=25,
其中甲品种山羊有25×25=10万只,乙品种山羊有25×35=15万只,
由频率估计概率,可得甲品种山羊达到售卖标准需要的养殖时间为6个月,7个月,8个月和
9个月的概率分别为0.2,0.35,0.35和0.1,
∴甲品种山羊要达到售卖标准需要养殖时间的期望为6×0.2+7×0.35+8×0.35+9×0.1=7.35(月).
由频率估计概率,可得乙品种山羊达到售卖标准需要的养殖时间为6个月,7个月,8个月和9个月的概率分别为0.1,0.3,0.4和0.2,
∴乙品种山羊要达到售卖标准需要养殖时间的期望为6×0.1+7×0.3+8×0.4+9×0.2=7.7(月)
养殖每只甲品种山羊利润的期望为2500−7.35×300=2500−2205=295 (元),
养殖每只乙品种山羊利润的期望为2700−7.7×300=2700−2310=390(元),
故2022年该县售卖的山羊所获利润的期望为10×295+15×390=8800(万元).
【考点】
求解线性回归方程
用频率估计概率
离散型随机变量的期望与方差
【解析】
无
无
【解答】
解:(1)∵x¯=1+2+3+4+5+66=3.5,
y¯=11+13+16+15+20+216=16 ,
∴b=−2.5×(−5)+(−1.5)×(−3)+(−0.5)×0+0.5×(−1)+1.5×4+2.5×5(−2.5)2+(−1.5)2+(−0.5)2+0.52+1.52+2.52
=3517.5=2,
可得a=16−2×3.5=9 ,
∴y与x之间的线性回归方程为y=2x+9.
(2)由(1)可知,当x=8时,可得y=25,
其中甲品种山羊有25×25=10万只,乙品种山羊有25×35=15万只,
由频率估计概率,可得甲品种山羊达到售卖标准需要的养殖时间为6个月,7个月,8个月和
9个月的概率分别为0.2,0.35,0.35和0.1,
∴甲品种山羊要达到售卖标准需要养殖时间的期望为6×0.2+7×0.35+8×0.35+9×0.1=7.35(月).
由频率估计概率,可得乙品种山羊达到售卖标准需要的养殖时间为6个月,7个月,8个月和9个月的概率分别为0.1,0.3,0.4和0.2,
∴乙品种山羊要达到售卖标准需要养殖时间的期望为6×0.1+7×0.3+8×0.4+9×0.2=7.7(月)
养殖每只甲品种山羊利润的期望为2500−7.35×300=2500−2205=295 (元),
养殖每只乙品种山羊利润的期望为2700−7.7×300=2700−2310=390(元),
故2022年该县售卖的山羊所获利润的期望为10×295+15×390=8800(万元).
【答案】
(1)证明:连接A1C,在△A1AC中,A1A=2,AC=1,∠A1AC=60∘,
由余弦定理得A1C=3,
所以A1C2+AC2=A1A2,
所以A1C⊥AC .
同理A1C⊥BC .
又因为BC∩AC=C,
所以A1C⊥平面ABC.
因为A1C⊂平面A1ACC1,
所以平面ABC⊥平面A1ACC1 .
(2)解:以C为坐标原点,CA→的方向为x轴的正方向,建立如图所示的空间直角坐标系C−xyz,
则A(1,0,0),B(−12,32,0),C(0,0,0,0),A1(0,0,3),P−13,0,33 .
AA1→=−1,0,3,AB→=−32,32,0,A1B→=−12,32,−3,
A1P→=−13,0,−233 .
设平面A1AB的法向量为m→=x1,y1,z1,
则 m→⋅AA1→=−x1+3z1=0,m→⋅AB→=−32x1+32y1=0,
令z1=1,得m→=3,3,1 .
设平面PA1B的法向量为n→=x2,y2,z2,
则n→⋅A1B→=−12x2+32y2−3z2=0,n⋅A1P→=−13x2−233z2=0,
令z2=1,得n→=−23,0,1,
所以csm→,n→=m→⋅n→|m→||n→|=−6+113×13=−513 .
因为二面角P−A1B−A为锐角,
所以二面角P−A1B−A的余弦值为513 .
【考点】
平面与平面垂直的判定
用空间向量求平面间的夹角
【解析】
此题暂无解析
【解答】
(1)证明:连接A1C,在△A1AC中,A1A=2,AC=1,∠A1AC=60∘,
由余弦定理得A1C=3,
所以A1C2+AC2=A1A2,
所以A1C⊥AC .
同理A1C⊥BC .
又因为BC∩AC=C,
所以A1C⊥平面ABC.
因为A1C⊂平面A1ACC1,
所以平面ABC⊥平面A1ACC1 .
(2)解:以C为坐标原点,CA→的方向为x轴的正方向,建立如图所示的空间直角坐标系C−xyz,
则A(1,0,0),B(−12,32,0),C(0,0,0,0),A1(0,0,3),P−13,0,33 .
AA1→=−1,0,3,AB→=−32,32,0,A1B→=−12,32,−3,
A1P→=−13,0,−233 .
设平面A1AB的法向量为m→=x1,y1,z1,
则 m→⋅AA1→=−x1+3z1=0,m→⋅AB→=−32x1+32y1=0,
令z1=1,得m→=3,3,1 .
设平面PA1B的法向量为n→=x2,y2,z2,
则n→⋅A1B→=−12x2+32y2−3z2=0,n⋅A1P→=−13x2−233z2=0,
令z2=1,得n→=−23,0,1,
所以csm→,n→=m→⋅n→|m→||n→|=−6+113×13=−513 .
因为二面角P−A1B−A为锐角,
所以二面角P−A1B−A的余弦值为513 .
【答案】
解:(1)∵e=ca=12,
∴a=2c,
∵椭圆上的点离右焦点F的最短距离为a−c=1 ,
∴a=2,c=1,b=3,
∴椭圆E的方程为x24+y23=1 .
(2)当P与F重合时,显然符合题意,
当P与F不重合时,设直线l的方程为x=my+1,A(x1,y1),B(x2,y2),P(t,0) ,
联立方程组x=my+1,3x2+4y2=12,
得3m2+4y2+6my−9=0,
则y1+y2=−6m3m+4,y1y2=−93m2+4,
∵|PA||PB|=|AF||BF|.
∴PF为∠APB的角平分线,
∴kPA+kPB=y1x1−t+y2x2−t=0 ,
即y1x2−t+y2x1−t=0 ,
整理得2my1y2+1−ty1+y2=0,
即2m⋅−93m2+4+1−t−6m3m2+4=0 ,
解得t=4,
故存在P1,0,P4,0满足题意.
【考点】
椭圆的标准方程
椭圆的定义和性质
椭圆的离心率
圆锥曲线的综合问题
【解析】
无
无
【解答】
解:(1)∵e=ca=12,
∴a=2c,
∵椭圆上的点离右焦点F的最短距离为a−c=1 ,
∴a=2,c=1,b=3,
∴椭圆E的方程为x24+y23=1 .
(2)当P与F重合时,显然符合题意,
当P与F不重合时,设直线l的方程为x=my+1,A(x1,y1),B(x2,y2),P(t,0) ,
联立方程组x=my+1,3x2+4y2=12,
得3m2+4y2+6my−9=0,
则y1+y2=−6m3m+4,y1y2=−93m2+4,
∵|PA||PB|=|AF||BF|.
∴PF为∠APB的角平分线,
∴kPA+kPB=y1x1−t+y2x2−t=0 ,
即y1x2−t+y2x1−t=0 ,
整理得2my1y2+1−ty1+y2=0,
即2m⋅−93m2+4+1−t−6m3m2+4=0 ,
解得t=4,
故存在P1,0,P4,0满足题意.
【答案】
解:(1)当a=12时,f(x)=lnx−x+12x2,
f′(x)=1x−1+x=x2−x+1x.
因为f′(1)=1,f(1)=−12,
所以所求切线方程为y−(−12)=1×(x−1),即2x−2y−3=0.
(2)因为f′(x)=x2−2ax+2ax,
所以x1,x2是方程x2−2ax+2a=0的两个正根.
令g(x)=x2−2ax+2a,
则Δ=4a2−8a>0,a>0,g(0)=2a>0,解得a>2.
因为x1+x2=x1x2=2a,
所以f(x2)−f(x1)
=2alnx2−2ax2+12x22−2alnx1−2ax1+12x12
=x1x2lnx2x1−12(x22−x12).
由f(x1)−f(x2)>b(x12−x22),
可得f(x2)−f(x1)−b(x22−x12)
=x1x2lnx2x1−12+b(x22−x12)<0.
因为x1x2>0,
所以lnx2x1−12+bx2x1−x1x2<0,
即12+bx2x1−x1x2−lnx2x1>0恒成立.
令t=x2x1,
因为x2>e2x1,
所以t>e2,
则12+bt−1t−lnt>0,
整理得12+b>lntt−1t=tlntt2−1.
令ℎ(t)=tlntt2−1,t>e2,
则ℎ′(t)=(lnt+1)(t2−1)−2t2lnt(t2−1)2,
=(t2−1)−(t2+1)lnt(t2−1)2<0,
所以ℎ(t)在(e2,+∞)上单调递减,
所以ℎ(t)<ℎ(e2)=2e2e4−1.
由b+12≥2e2e4−1,
解得b≥2e2e4−1−12=−e4+4e2+12(e4−1),
故b的取值范围是−e4+4e2+12(e4−1),+∞.
【考点】
利用导数研究曲线上某点切线方程
利用导数研究不等式恒成立问题
【解析】
无
无
【解答】
解:(1)当a=12时,f(x)=lnx−x+12x2,
f′(x)=1x−1+x=x2−x+1x.
因为f′(1)=1,f(1)=−12,
所以所求切线方程为y−(−12)=1×(x−1),即2x−2y−3=0.
(2)因为f′(x)=x2−2ax+2ax,
所以x1,x2是方程x2−2ax+2a=0的两个正根.
令g(x)=x2−2ax+2a,
则Δ=4a2−8a>0,a>0,g(0)=2a>0,解得a>2.
因为x1+x2=x1x2=2a,
所以f(x2)−f(x1)
=2alnx2−2ax2+12x22−2alnx1−2ax1+12x12
=x1x2lnx2x1−12(x22−x12).
由f(x1)−f(x2)>b(x12−x22),
可得f(x2)−f(x1)−b(x22−x12)
=x1x2lnx2x1−12+b(x22−x12)<0.
因为x1x2>0,
所以lnx2x1−12+bx2x1−x1x2<0,
即12+bx2x1−x1x2−lnx2x1>0恒成立.
令t=x2x1,
因为x2>e2x1,
所以t>e2,
则12+bt−1t−lnt>0,
整理得12+b>lntt−1t=tlntt2−1.
令ℎ(t)=tlntt2−1,t>e2,
则ℎ′(t)=(lnt+1)(t2−1)−2t2lnt(t2−1)2,
=(t2−1)−(t2+1)lnt(t2−1)2<0,
所以ℎ(t)在(e2,+∞)上单调递减,
所以ℎ(t)<ℎ(e2)=2e2e4−1.
由b+12≥2e2e4−1,
解得b≥2e2e4−1−12=−e4+4e2+12(e4−1),
故b的取值范围是−e4+4e2+12(e4−1),+∞.
【答案】
解:(1)由x=1−t,y=−1+2t得2x+y−1=0,
即直线l的普通方程为2x+y−1=0.
由ρ2=12sin2θ+3,得ρ2sin2θ+3ρ2=12.
∵y=ρsinθ,x2+y2=ρ2,3x2+4y2=12,
故曲线C的直角坐标方程为x24+y23=1.
(2)直线l的参数方程为x=1−t,y=−1+2t(t为参数),
化为标准形式x=1−55t,y=−1+255t(t为参数),
代入3x2+4y2=12,得19t2−225t−25=0.
设A,B对应的参数分别为t1,t2,
则t1+t2=22519,t1t2=−2519<0.
可知t1,t2异号,
所以1|PA|+1|PB|=|PA|+|PB||PA||PB|=|t1|+|t2||t1t2|=|t1−t2||t1t2|.
因为|t1−t2|=t1+t22−4t1t2=123019,
所以1|PA|+1|PB|=123025.
【考点】
参数方程与普通方程的互化
椭圆的极坐标方程与直角坐标方程的互化
参数方程的优越性
【解析】
无
无
【解答】
解:(1)由x=1−t,y=−1+2t得2x+y−1=0,
即直线l的普通方程为2x+y−1=0.
由ρ2=12sin2θ+3,得ρ2sin2θ+3ρ2=12.
∵y=ρsinθ,x2+y2=ρ2,3x2+4y2=12,
故曲线C的直角坐标方程为x24+y23=1.
(2)直线l的参数方程为x=1−t,y=−1+2t(t为参数),
化为标准形式x=1−55t,y=−1+255t(t为参数),
代入3x2+4y2=12,得19t2−225t−25=0.
设A,B对应的参数分别为t1,t2,
则t1+t2=22519,t1t2=−2519<0.
可知t1,t2异号,
所以1|PA|+1|PB|=|PA|+|PB||PA||PB|=|t1|+|t2||t1t2|=|t1−t2||t1t2|.
因为|t1−t2|=t1+t22−4t1t2=123019,
所以1|PA|+1|PB|=123025.
【答案】
解:(1)当t=1时,fx=|x−2|−|x+1| .
当x<−1时,−x+2+x+1=3≥1恒成立,所以x<−1 ;
当1≤x≤2时,由−x+2−x−1≥1,x≤0,所以−1≤x≤0 ;
x≥2时,x−2−x−1≥1不成立 .
所以不等式fx≥1的解集为(−∞,0].
(2)因为t2≥f(x)对任意的x∈R恒成立,所以t2≥fxmax .
因为fx=|x−2t|−|x+t|≤|x−2t−x−t|=3|t|,
所以t2≥3|t|.
因为t>0,所以t≥3 .
M=t+t+8t−1=t−1+9t−1+2≥29+2=8 .
当且仅当t−1=9t−1,即t=4时取等号,
所以M的最小值为8.
【考点】
绝对值不等式
三角不等式
基本不等式
函数恒成立问题
【解析】
【解答】
解:(1)当t=1时,fx=|x−2|−|x+1| .
当x<−1时,−x+2+x+1=3≥1恒成立,所以x<−1 ;
当1≤x≤2时,由−x+2−x−1≥1,x≤0,所以−1≤x≤0 ;
x≥2时,x−2−x−1≥1不成立 .
所以不等式fx≥1的解集为(−∞,0].
(2)因为t2≥f(x)对任意的x∈R恒成立,所以t2≥fxmax .
因为fx=|x−2t|−|x+t|≤|x−2t−x−t|=3|t|,
所以t2≥3|t|.
因为t>0,所以t≥3 .
M=t+t+8t−1=t−1+9t−1+2≥29+2=8 .
当且仅当t−1=9t−1,即t=4时取等号,
所以M的最小值为8.年份
2015
2016
2017
2018
2019
2020
年份代码x
1
2
3
4
5
6
售卖山羊y(万只)
11
13
16
15
20
21
养殖时间(月数)
6
7
8
9
甲品种山羊(只)
20
35
35
10
乙品种山羊(只)
10
30
40
20
2020-2021学年河南省南阳市高三(上)1月月考数学(理)试卷北师大版: 这是一份2020-2021学年河南省南阳市高三(上)1月月考数学(理)试卷北师大版,共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年河南省南阳市高三(上)9月考前适应性考试数学(理)试卷北师大版: 这是一份2020-2021学年河南省南阳市高三(上)9月考前适应性考试数学(理)试卷北师大版,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年河南省南阳市高三(上)11月月考数学(理)试卷北师大版: 这是一份2020-2021学年河南省南阳市高三(上)11月月考数学(理)试卷北师大版,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












