2022届新高考一轮复习苏教版 第6章 第3讲 平面向量的数量积及平面向量的应用 课件（63张）

这是一份2022届新高考一轮复习苏教版 第6章 第3讲 平面向量的数量积及平面向量的应用 课件（63张），共60页。PPT课件主要包含了栏目导航，基础整合自测纠偏，素养微专直击高考，重难突破能力提升，配套训练，∠AOB，acosθ，bcosθ，λa·b，a·λb等内容，欢迎下载使用。

|a||b|·cs θ　
3．平面向量数量积的运算律(1)交换律：a·b＝b·a；(2)数乘结合律：(λa)·b＝________＝________；(3)分配律：a·(b＋c)＝________.
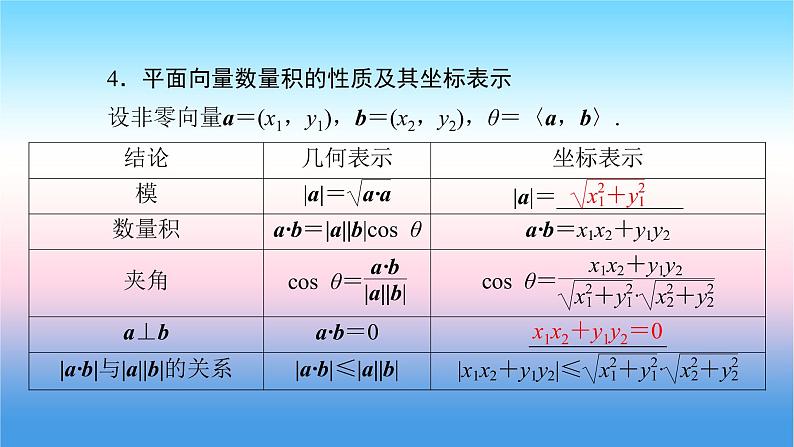
4．平面向量数量积的性质及其坐标表示设非零向量a＝(x1，y1)，b＝(x2，y2)，θ＝〈a，b〉.
x1x2＋y1y2＝0　
【常用结论】1．平面向量数量积运算的常用公式(1)(a＋b)·(a－b)＝a2－b2；(2)(a±b)2＝a2±2a·b＋b2.2．两个向量a，b的夹角为锐角⇔a·b＞0且a，b不共线；两个向量a，b的夹角为钝角⇔a·b＜0且a，b不共线．
3．(2019年哈尔滨模拟)已知向量a＝(k,6)，b＝(－2,3)，且a⊥b，则k的值是(　　)A．－4B．－3C．4D．9【答案】D
5．(教材改编)已知|a|＝5，|b|＝4，a与b的夹角θ＝120°，则向量b在向量a方向上的投影为________．【答案】－2　
6．(2020年郑州模拟)已知a＝(1,1)，b＝(2，m)，a⊥(a－b)，则|b|＝______.【答案】2　【解析】因为已知a＝(1,1)，b＝(2，m)，a⊥(a－b)，所以a·(a－b)＝a2－a·b＝0，所以a2＝a·b，即2＝2＋m，所以m＝0，所以b＝(2,0)，则|b|＝2.
对于实数a，b，c有(a·b)·c＝a·(b·c)，但对于向量a，b，c而言，(a·b)·c＝a·(b·c)不一定成立，即不满足向量结合律．这是因为(a·b)·c表示一个与c共线的向量，而a·(b·c)表示一个与a共线的向量，而a与c不一定共线，所以(a·b)·c＝a·(b·c)不一定成立．
【答案】(1)√　(2)√　(3)×　(4)×　(5)×　(6)×
【解题技巧】1．求两个向量的数量积有三种方法：利用定义、利用向量的坐标运算、利用数量积的几何意义．2．解决涉及几何图形的向量数量积运算问题时，可先利用向量的加减运算或数量积的运算律化简再运算．但一定要注意向量的夹角与已知平面角的关系是相等还是互补．
【答案】(1)A　(2)B　
【解题技巧】1．题目条件给出向量的坐标中含有三角函数的形式，运用向量共线或垂直或等式成立得到三角函数的关系式，然后求解．2．给出用三角函数表示的向量坐标，要求的是向量的模或者其他向量的表达形式，解题思路是经过向量的运算，利用三角函数在定义域内的有界性，求得值域等．
【解题技巧】物理学中的受力分析、速度分解与合成，特别是进行正交分解，充分体现了平面向量基本定理的思想内涵，使复杂的问题简单化、特殊化，从而便于解决．
【变式精练】4．已知F＝(2,3)作用一物体，使物体从A(2,0)移动到B(4,0)，则力F对物体所做的功为________．【答案】4　
图形化策略，指解决向量问题时，利用图形语言翻译已知条件和所求结论，借助图形思考解决问题，利用此种策略方法，各种数量关系在图形中非常明了，能起到事半功倍的作用．代数化策略，指解决向量问题时，利用代数语言翻译已知条件和所求结论，借助代数运算解决所面临的问题，通过平面向量基本定理演变而来的代数运算和坐标化的代数运算．
思想方法类——求解平面向量数量积最值问题的两种策略
【解题技巧】方法一用了图形化策略，采用坐标化思想，将所求的模赋予明显的几何意义，利用数形结合思想求解最值或直接弄清所求的模表示的几何意义，结合动点表示的图形求解．方法二和方法三用了代数化策略，利用平方技巧找到向量的模的表达式，把所求的模表示成某个变量的函数，用最值方法求解．