2021-2022学年江苏省南京市高三（上）零模考前数学试卷

这是一份2021-2022学年江苏省南京市高三（上）零模考前数学试卷，共23页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

1．（5分）已知复数z＝1+i，设复数w＝，则w的虚部是（ ）
A．﹣1B．1C．iD．﹣i
2．（5分）已知a，b为非零实数，则“a＜b”是“”的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件
3．（5分）在△ABC中，＝，++＝，＝λ，则λ＝（ ）
A．B．1C．2D．3
4．（5分）棱长为a的正方体ABCD﹣A1B1C1D1中，点E，F，G分别为棱AB，CC1，C1D1的中点，则过E，F，G三点的平面截正方体所得截面面积为（ ）
A．B．C．D．
5．（5分）若θ为锐角，cs（）＝，则tanθ+＝（ ）
A．B．C．D．
6．（5分）将正整数12分解成两个正整数的乘积有1×12，2×6，3×4三种，其中3×4是这三种分解中两数差的绝对值最小的，我们称3×4为12的最佳分解．当p×q（p，q∈N*）是正整数n的最佳分解时，我们定义函数f（n）＝|p﹣q|，例如f（12）＝|4﹣3|＝1，则＝（ ）
A．21011﹣1B．21011 C．21010﹣1D．21010
7．（5分）过点M（p，0）作倾斜角为150°的直线与抛物线C：y2＝2px（p＞0）交于两点A，B，若|AB|＝2，则|AM|•|BM|的值为（ ）
A．4B．4C．2D．4
8．（5分）已知a＞1，b＞1，且＝，则下列结论一定正确的是（ ）
A．ln（a+b）＞2B．ln（a﹣b）＞0C．2a+1＜2bD．2a+2b＜23
二、多项选择题（本大题共4小题，每题5分，共20分每题全选对的得5分，部分选对的得2分，有选错的得0分）
9．（5分）已知函数f（x）＝2sin（ωx+φ）（ω＞0，0＜φ＜π）图象的一条对称轴为x＝，f（）＝且f（x）在（，）内单调递减，则以下说法正确的是（ ）
A．（﹣，0）是其中一个对称中心
B．
C．f（x）在（﹣，0）单调递增
D．f（﹣）＝﹣1
10．（5分）在△ABC中，角A，B，C所对的边分别为a，b，c，且C＝，将△ABC分别绕边a，b，c所在的直线旋转一周，形成的几何体的体积分别记为Va，Vb，Vc，侧面积分别记为Sa，Sb，Sc，则（ ）
A．Va+Vb≥2VcB．Sa+Sb≥2Sc
C．D．
11．（5分）设集合S，T，S⊆N*，T⊆N*，S，T中至少有2个元素，且S，T满足：
①对于任意的x，y∈S，若x≠y，则xy∈T；
②对于任意的x，y∈T，若x＜y，则∈S．下列命题正确的是（ ）
A．若S有4个元素，则S∪T有7个元素
B．若S有4个元素，则S∪T有6个元素
C．若S有3个元素，则S∪T有5个元素
D．若S有3个元素，则S∪T有4个元素
12．（5分）甲、乙两人进行围棋比赛，共比赛2n（n∈N*）局，且每局甲获胜的概率和乙获胜的概率均为．如果某人获胜的局数多于另一人，则此人赢得比赛．记甲赢得比赛的概率为P（n），则（ ）
A．B．
C．D．P（n）的最大值为
三、填空题（本大题共4小题，每题5分，共20分）
13．（5分）已知f（x）＝tanx（ex+e﹣x）+6，f（t）＝8，则f（﹣t）＝ ．
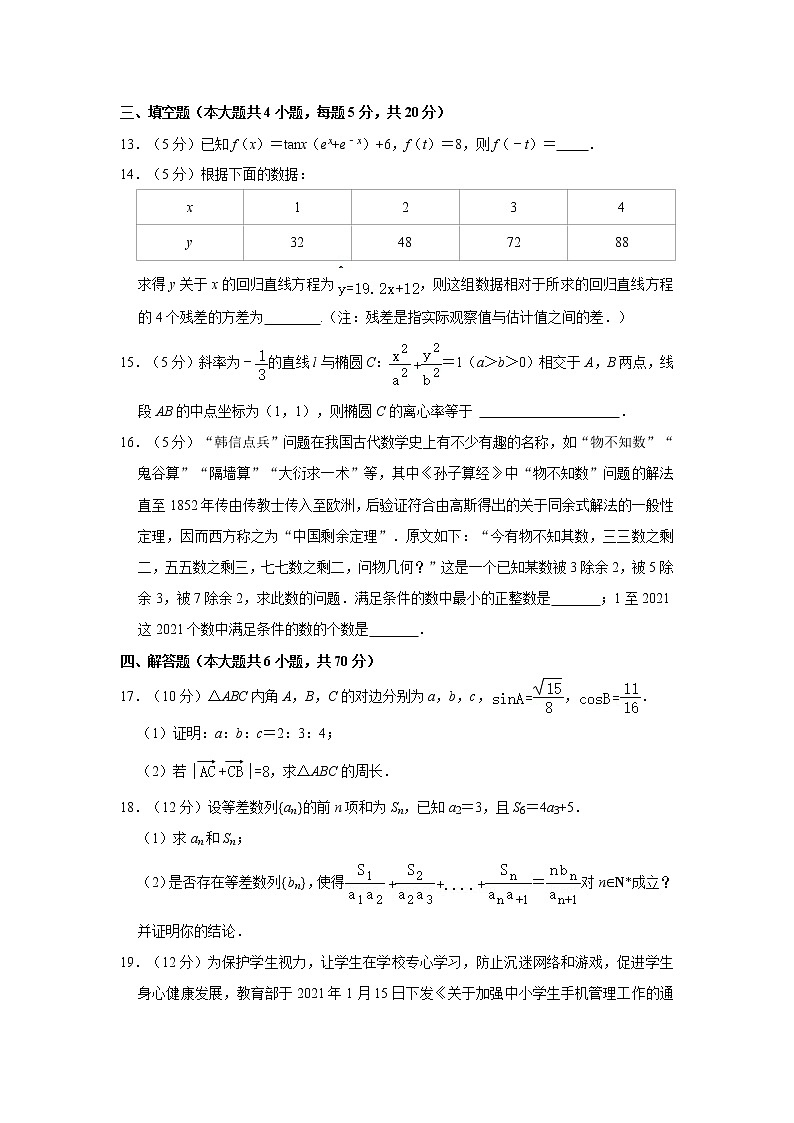
14．（5分）根据下面的数据：
求得y关于x的回归直线方程为，则这组数据相对于所求的回归直线方程的4个残差的方差为 .（注：残差是指实际观察值与估计值之间的差．）
15．（5分）斜率为﹣的直线l与椭圆C：＝1（a＞b＞0）相交于A，B两点，线段AB的中点坐标为（1，1），则椭圆C的离心率等于 ．
16．（5分）“韩信点兵”问题在我国古代数学史上有不少有趣的名称，如“物不知数”“鬼谷算”“隔墙算”“大衍求一术”等，其中《孙子算经》中“物不知数”问题的解法直至1852年传由传教士传入至欧洲，后验证符合由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”．原文如下：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”这是一个已知某数被3除余2，被5除余3，被7除余2，求此数的问题．满足条件的数中最小的正整数是 ；1至2021这2021个数中满足条件的数的个数是 ．
四、解答题（本大题共6小题，共70分）
17．（10分）△ABC内角A，B，C的对边分别为a，b，c，，．
（1）证明：a：b：c＝2：3：4；
（2）若，求△ABC的周长．
18．（12分）设等差数列{an}的前n项和为Sn，已知a2＝3，且S6＝4a3+5．
（1）求an和Sn；
（2）是否存在等差数列{bn}，使得＝对n∈N*成立？并证明你的结论．
19．（12分）为保护学生视力，让学生在学校专心学习，防止沉迷网络和游戏，促进学生身心健康发展，教育部于2021年1月15日下发《关于加强中小学生手机管理工作的通知》，对中小学生的手机使用和管理作出了相关的规定．某研究型学习小组调查研究“中学生使用智能手机对学习的影响”，现对我校80名学生调查得到统计数据如下表，记A为事件：“学习成绩优秀且不使用手机”；B为事件：“学习成绩不优秀且不使用手机”，且已知事件A的频率是事件B的频率的2倍．
（1）运用独立性检验思想，判断是否有99.5%的把握认为中学生使用手机对学习成绩有影响？
（2）采用分层抽样的方法从这80名学生中抽出6名学生，并安排其中3人做书面发言，记做书面发言的成绩优秀的学生数为X，求X的分布列和数学期望．
参考数据：，其中n＝a+b+c+d．
20．（12分）如图，四棱柱ABCD﹣A1B1C1D1中，面ABB1A1⊥面ABCD，面ADD1A1⊥面ABCD，点E、M、N分别是棱AA1、BC、CD的中点．
（1）证明：AA1⊥面ABCD．
（2）若四边形ABCD是边长为2的正方形，且AA1＝AD，面EMN∩面ADD1A1＝直线l，求直线l与B1C所成角的余弦值．
21．（12分）已知双曲线E：﹣＝1（a＞0，b＞0）过点D（3，1），且该双曲线的虚轴端点与两顶点A1，A2的张角为120°．
（1）求双曲线E的方程；
（2）过点B（0，4）的直线1与双曲线E左支相交于点M，N，直线DM，DN与y轴相交于P，Q两点，求|BP|+|BQ|的取值范围．
22．（12分）已知函数f（x）＝（x﹣1）（aex﹣1）在x＝1处的切线方程为y＝（e﹣1）（x﹣1）．
（1）求a的值；
（2）若方程f（x）＝b有两个不同实根x1、x2，证明：．
2021-2022学年江苏省南京市高三（上）零模考前数学试卷
参考答案与试题解析
一、单项选择题（本大题共8小题，每题5分，共40分）
1．（5分）已知复数z＝1+i，设复数w＝，则w的虚部是（ ）
A．﹣1B．1C．iD．﹣i
【分析】利用复数的运算法则、共轭复数的定义、虚部的定义即可得出．
【解答】解：复数z＝1+i，
复数w＝＝＝＝＝﹣1﹣i，
则w的虚部是﹣1，
故选：A．
2．（5分）已知a，b为非零实数，则“a＜b”是“”的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件
【分析】构造函数f（x）＝x|x|，利用函数的奇偶性和单调性判断即可．
【解答】解：设f（x）＝x|x|，则f（x）为奇函数且在（0，+∞），（﹣∞，0）上为增函数，
∴a＜b⇔a|a|＜b|b|⇔＜，
∴a＜b是的充要条件，
故选：C．
3．（5分）在△ABC中，＝，++＝，＝λ，则λ＝（ ）
A．B．1C．2D．3
【分析】由题意可得点D为BC的中点，由向量的线性运算可得+＝，从而可得2＝，即可求得λ的值．
【解答】解：因为＝，所以点D为BC的中点，
因为++＝，
所以+＝﹣＝，即2＝，
所以λ＝2．
故选：C．
4．（5分）棱长为a的正方体ABCD﹣A1B1C1D1中，点E，F，G分别为棱AB，CC1，C1D1的中点，则过E，F，G三点的平面截正方体所得截面面积为（ ）
A．B．C．D．
【分析】取BC中点P，A1D1中点M，AA1中点N，连结EP、PF、FG、GM、MN、NE，推导出过E，F，G三点的平面截正方体所得截面为正六边形EPFGMNE，由此能求出过E，F，G三点的平面截正方体所得截面面积．
【解答】解：取BC中点P，A1D1中点M，AA1中点N，连结EP、PF、FG、GM、MN、NE，
则EP∥MG，PF∥MN，GF∥EN，
且EP＝PF＝FG＝GM＝MN＝HE＝＝，
∴六边形EPFGMNE是正六边形，
∴过E，F，G三点的平面截正方体所得截面为正六边形EPFGMNE，
∴过E，F，G三点的平面截正方体所得截面面积为：
6×（）＝．
故选：C．
5．（5分）若θ为锐角，cs（）＝，则tanθ+＝（ ）
A．B．C．D．
【分析】由θ为锐角，cs（）＝，运用三角函数的同角公式，可得，进而可得 的值，再结合正切函数的两角差公式，即可求解．
【解答】解：∵θ为锐角，cs（）＝，
又∵，
∴，
∴，
∵＝，
∴．
故选：B．
6．（5分）将正整数12分解成两个正整数的乘积有1×12，2×6，3×4三种，其中3×4是这三种分解中两数差的绝对值最小的，我们称3×4为12的最佳分解．当p×q（p，q∈N*）是正整数n的最佳分解时，我们定义函数f（n）＝|p﹣q|，例如f（12）＝|4﹣3|＝1，则＝（ ）
A．21011﹣1B．21011 C．21010﹣1D．21010
【分析】n为偶数时，f（2i）＝0；n为奇数时，f（2i）＝2，把数列{f（2i）}的前2021项和转化为等比数列求和即可．
【解答】解：当i＝2时，f（22）＝f（2×2）＝|2﹣2|＝0，
当i＝4时，f（24）＝f（22×22）＝22﹣22＝0，…，
所以i为偶数时，f（2i）＝0；
当i＝1时，f（21）＝f（1×2）＝2﹣1＝1，
当i＝3时，f（23）＝f（2×22）＝|22﹣2|＝1×2，…，
所以i为奇数时，f（2i）＝2，
所以＝f（2）+f（22）+f（23）+f（24）+…+f（22021）
＝f（2）+f（23）+…+f（22019）+f（22021）
＝20+21+…+21011
＝
＝21011﹣1．
故选：A．
7．（5分）过点M（p，0）作倾斜角为150°的直线与抛物线C：y2＝2px（p＞0）交于两点A，B，若|AB|＝2，则|AM|•|BM|的值为（ ）
A．4B．4C．2D．4
【分析】由题意可得，直线AB的方程为，联立直线与抛物线方程，整理可得，再结合韦达定理和两点之间的距离公式，即可求解．
【解答】解：由题意可得，直线AB的方程为，
联立直线与抛物线方程，整理可得，
设A（x1，y1），B（x2，y2），
由韦达定理可得，y1+y2＝，y1y2＝﹣2p2，
又∵，
∴|AB|＝＝＝＝＝2，
∴，
∵点M（p，0），A（x1，y1），B（x2，y2），
∴|AM|•|BM|＝＝4|y1y2|＝8p2＝4．
故选：A．
8．（5分）已知a＞1，b＞1，且＝，则下列结论一定正确的是（ ）
A．ln（a+b）＞2B．ln（a﹣b）＞0C．2a+1＜2bD．2a+2b＜23
【分析】令f（x）＝，x∈（0，+∞），利用导数研究函数的单调性即可判断出结论．
【解答】解：令f（x）＝，x∈（0，+∞），
f′（x）＝，
可得x＞1时，函数f（x）单调递增，
∵a＞1，b＞1，且＝＝+，，
∴﹣＝∈（0，），
∴a＞b+1，
∴Ln（a﹣b）＞0，因此B正确；
∴ln（a+b）＞ln（2b+1）＞ln3，ln（a+b）＞2不一定成立，因此A不正确；
2a+1＞2b+2＞2b，因此C不正确；
2a+2b＞2b+1+2b＝3×2b．因此2a+2b＜23不一定成立，因此不正确．
故选：B．
二、多项选择题（本大题共4小题，每题5分，共20分每题全选对的得5分，部分选对的得2分，有选错的得0分）
9．（5分）已知函数f（x）＝2sin（ωx+φ）（ω＞0，0＜φ＜π）图象的一条对称轴为x＝，f（）＝且f（x）在（，）内单调递减，则以下说法正确的是（ ）
A．（﹣，0）是其中一个对称中心
B．
C．f（x）在（﹣，0）单调递增
D．f（﹣）＝﹣1
【分析】分别根据三角函数对称轴、对称中心、单调性的性质，以及将x＝代入f（x），即可求解．
【解答】解：由题意可得f（x）关于x＝对称，f（）＝且f（x）在（，）内单调递减，
∴，
∴，故B选项错误，
∵，
∴，
∴（﹣，0）是其中一个对称中心，故A选项正确，
∵，k∈Z
∴，k∈Z
∴当k＝0时，f（x）在 上单调递增，故C选项错误，
，故D选项正确，
故选：AD．
10．（5分）在△ABC中，角A，B，C所对的边分别为a，b，c，且C＝，将△ABC分别绕边a，b，c所在的直线旋转一周，形成的几何体的体积分别记为Va，Vb，Vc，侧面积分别记为Sa，Sb，Sc，则（ ）
A．Va+Vb≥2VcB．Sa+Sb≥2Sc
C．D．
【分析】如图所示，过点C作CD⊥AB，垂足为D，设CD＝h，则h＝．分别计算出体积Va，Vb，Vc，侧面积Sa，Sb，Sc.通过作差即可比较出大小关系．
【解答】解：如图所示，过点C作CD⊥AB，垂足为D，设CD＝h，则h＝，c2＝a2+b2．
由题意可得：Va＝×πb2×a，Vb＝πa2b，Vc＝π×c＝π，
∴Va+Vb﹣2Vc＝ab（a+b﹣）≥ab（2﹣）＝ab（2﹣）＞0，因此A正确；
+＝（+），＝＝（+），
∴+＝，因此C正确．
侧面积分别记为Sa＝πbc，Sb＝πac，Sc＝．
Sa+Sb﹣2Sc＝π[bc+ac﹣]＝π≥0，因此B正确；
+＝（+）＝，＝•（a2+b2），
+﹣＝＜0，∴+＜，因此D不正确．
故选：ABC．
11．（5分）设集合S，T，S⊆N*，T⊆N*，S，T中至少有2个元素，且S，T满足：
①对于任意的x，y∈S，若x≠y，则xy∈T；
②对于任意的x，y∈T，若x＜y，则∈S．下列命题正确的是（ ）
A．若S有4个元素，则S∪T有7个元素
B．若S有4个元素，则S∪T有6个元素
C．若S有3个元素，则S∪T有5个元素
D．若S有3个元素，则S∪T有4个元素
【分析】利用特殊集合排除选项，推出结果即可．
【解答】解：取：S＝{1，2，4}，则T＝{2，4，8}，S∪T＝{1，2，4，8}，4个元素，排除C．
S＝{2，4，8}，则T＝{8，16，32}，S∪T＝{2，4，8，16，32}，5个元素，排除D；
S＝{2，4，8，16}则T＝{8，16，32，64，128}，S∪T＝{2，4，8，16，32，64，128}，7个元素，排除B；
故选：A．
12．（5分）甲、乙两人进行围棋比赛，共比赛2n（n∈N*）局，且每局甲获胜的概率和乙获胜的概率均为．如果某人获胜的局数多于另一人，则此人赢得比赛．记甲赢得比赛的概率为P（n），则（ ）
A．B．
C．D．P（n）的最大值为
【分析】若甲、乙比赛4局甲获胜，则甲在4局比赛中至少胜3局，利用相互独立事件概率乘法公式能求出P（2）；若甲、乙比赛6局甲获胜，则甲在6局比赛中至少胜4局，利用相互独立事件概率乘法公式能求出P（3）；在2n局比赛中甲获胜，则甲胜的局数至少为n+1局，利用相互独立事件概率乘法公式得P（n）＝+•••+＝；由P（n）＝，知当n＝1时，P（n）取最小值．
【解答】解：若甲、乙比赛4局甲获胜，则甲在4局比赛中至少胜3局，
∴P（2）＝＝，故A错误；
若甲、乙比赛6局甲获胜，则甲在6局比赛中至少胜4局，
∴P（3）＝＝，故B正确；
在2n局比赛中甲获胜，则甲胜的局数至少为n+1局，
∴P（n）＝+•••+
＝（）•（）2n
＝＝，故C正确；
∵P（n）＝，∴当n＝1时，P（n）取最小值，故D错误．
故选：BC．
三、填空题（本大题共4小题，每题5分，共20分）
13．（5分）已知f（x）＝tanx（ex+e﹣x）+6，f（t）＝8，则f（﹣t）＝ 4 ．
【分析】由已知代入可得f（﹣x）+f（x）＝12，然后代入即可求解．
【解答】解：f（x）＝tanx（ex+e﹣x）+6，f（t）＝8，
所以f（﹣x）+f（x）＝tanx（ex+e﹣x）+6﹣tanx（ex+e﹣x）+6＝12，
因为f（t）＝8，
所以f（﹣t）＝4．
故答案为：4．
14．（5分）根据下面的数据：
求得y关于x的回归直线方程为，则这组数据相对于所求的回归直线方程的4个残差的方差为 3.2 .（注：残差是指实际观察值与估计值之间的差．）
【分析】先求出估计值，然后求出残差，求出残差的平均数，利用方差的计算公式求解即可．
【解答】解：将x＝1，2，3，4代入回归方程可得的值依次为31.2，50.4，69.6，88.8，
所以残差分别为：0.8，﹣2.4，2.4，﹣0.8，
则残差的平均数为0，
所以残差的方差为．
故答案为：3.2．
15．（5分）斜率为﹣的直线l与椭圆C：＝1（a＞b＞0）相交于A，B两点，线段AB的中点坐标为（1，1），则椭圆C的离心率等于 ．
【分析】利用点差法，结合（1，1）是线段BA的中点，斜率为﹣，即可求出椭圆C的离心率．
【解答】解：设A（x1，y1），B（x2，y2），
则+＝1①，+＝1②，
因为（1，1）是线段AB的中点，
所以（x1+x2）＝1，（y1+y2）＝1，
因为直线AB的方程为y＝﹣（x﹣1）+1，
所以y1﹣y2＝﹣（x1﹣x2），
①②两式相减可得（x12﹣x22）+（y12﹣y22）＝0，
所以（x1﹣x2）（x1+x2）+（y1﹣y2）（y1+y2）＝0，
所以2×（x1﹣x2）+2×（y1﹣y2）＝0，
所以有＝，
所以e2＝1﹣＝，
所以e＝，
故答案为：．
16．（5分）“韩信点兵”问题在我国古代数学史上有不少有趣的名称，如“物不知数”“鬼谷算”“隔墙算”“大衍求一术”等，其中《孙子算经》中“物不知数”问题的解法直至1852年传由传教士传入至欧洲，后验证符合由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”．原文如下：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”这是一个已知某数被3除余2，被5除余3，被7除余2，求此数的问题．满足条件的数中最小的正整数是 23 ；1至2021这2021个数中满足条件的数的个数是 20 ．
【分析】推导出满足条件的一个数为15×2+21×3+70×2＝233，用 233 除以 3，5，7 三个数的最小公倍数 105，得到余数 23，由此求出将1至2021这2021个数中满足条件的数．
【解答】解：从3和5的公倍数中找出被7 除余1 的最小数15，
从3和7的公倍数中找出被 5 除余1 的最小数21，
最后从5和7的公倍数中找出除3 余1 的最小数70，
用15乘以2（2为最终结果除以7 的余数），
用21乘以3（3为最终结果除以5 的余数），
同理，用70乘以2（2为最终结果除以3 的余数），
然后把三个乘积相加，
即15×2+21×3+70×2＝233，
用 233 除以 3，5，7 三个数的最小公倍数 105，得到余数 23，
同理可得余下的数（前后两个数的差为105）
∴将1至2017这2017个数中满足条件的数依次为：
23，128，233，338，443，548，653，758，863，968，1073，1178，1283，1388，1493，
1598，1703，1808，1913，2018共有20个，
故答案为：23，20．
四、解答题（本大题共6小题，共70分）
17．（10分）△ABC内角A，B，C的对边分别为a，b，c，，．
（1）证明：a：b：c＝2：3：4；
（2）若，求△ABC的周长．
【分析】（1）利用同角三角函数基本关系式可求sinB，csA，利用两角和的正弦公式可求sinC的值，进而根据正弦定理即可证明．
（2）由（1）利用两角和的余弦公式可求csC的值，将已知等式平方，设a＝2t，b＝3t，c＝4t，利用平面向量数量积的运算即可求解．
【解答】解：（1）证明：，
∴A＜B，A为锐角，，
∴，
由正弦定理可得，得证．
（2）由（1）知，
∵，
∴，
设a＝2t，b＝3t，c＝4t，则，解得t＝2，
∴△ABC的周长为9t＝18．
18．（12分）设等差数列{an}的前n项和为Sn，已知a2＝3，且S6＝4a3+5．
（1）求an和Sn；
（2）是否存在等差数列{bn}，使得＝对n∈N*成立？并证明你的结论．
【分析】（1）根据等差数列的通项公式和求和公式即可求出首项和公差，可得通项公式和求和公式；
（2）存在等差数列{bn}满足条件，其中bn＝，n∈N*，用数学归纳法证明即可．
【解答】解：（1）设数列{an}的公差为d，则，
解得a1＝1，d＝2，
∴an＝2n﹣1，n∈N*，
∴Sn＝＝n2；
（2）设Tn＝，由＝可得b1＝1，
由T2＝+＝b2可得b2＝，
故存在等差数列{bn}满足条件，其中bn＝，n∈N*，
下面用数学归纳法证明：当bn＝时，Tn＝对n∈N*成立，
①当n＝1时，由上面过程可知，等式成立，
②假设n＝k时等式成立，即Tk＝＝，
则当n＝k+1时，Tk+1＝Tk+＝+＝，
＝＝＝＝，即当n＝k+1时等式成立，
由①②可知＝，（其中bn＝）对n∈N*成立．
19．（12分）为保护学生视力，让学生在学校专心学习，防止沉迷网络和游戏，促进学生身心健康发展，教育部于2021年1月15日下发《关于加强中小学生手机管理工作的通知》，对中小学生的手机使用和管理作出了相关的规定．某研究型学习小组调查研究“中学生使用智能手机对学习的影响”，现对我校80名学生调查得到统计数据如下表，记A为事件：“学习成绩优秀且不使用手机”；B为事件：“学习成绩不优秀且不使用手机”，且已知事件A的频率是事件B的频率的2倍．
（1）运用独立性检验思想，判断是否有99.5%的把握认为中学生使用手机对学习成绩有影响？
（2）采用分层抽样的方法从这80名学生中抽出6名学生，并安排其中3人做书面发言，记做书面发言的成绩优秀的学生数为X，求X的分布列和数学期望．
参考数据：，其中n＝a+b+c+d．
【分析】（1）根据所给的数据补全列联表，再由列联表中的数据，计算K2的值，对照临界表中的数据，比较即可得到答案；
（2）先求出随机变量X的可能取值，然后求出其对应的概率，列出分布列，由数学期望的计算公式求解即可．
【解答】解：（1）由题意可知，，解得a＝28，b＝14，
所以2×2列联表如下：
所以K2＝，
故有99.5%的把握认为中学生使用手机对学习有影响；
（2）根据题意，由分层抽样可知，抽取成绩优秀的学生3名，成绩不优秀的学生3名，
所以X的可能取值为0，1，2，3，
则P（X＝0）＝＝，
P（X＝1）＝＝，
P（X＝2）＝＝，
P（X＝3）＝＝，
所以X的分布列为：
故E（X）＝0×+1×+2×+3×＝．
20．（12分）如图，四棱柱ABCD﹣A1B1C1D1中，面ABB1A1⊥面ABCD，面ADD1A1⊥面ABCD，点E、M、N分别是棱AA1、BC、CD的中点．
（1）证明：AA1⊥面ABCD．
（2）若四边形ABCD是边长为2的正方形，且AA1＝AD，面EMN∩面ADD1A1＝直线l，求直线l与B1C所成角的余弦值．
【分析】（1）在面ABCD内，过点C作CP⊥AB于P，作CQ⊥AD于Q，再结合面面垂直的性质定理，线面垂直的性质定理和判定定理，得证；
（2）设MN∩AD＝F，连接EF，可证直线EF即为直线l，再以A为原点建立空间直角坐标系，由cs＜，＞＝，得解．
【解答】（1）证明：在面ABCD内，过点C作CP⊥AB于P，作CQ⊥AD于Q，
∵面ABB1A1⊥面ABCD，面ABB1A1∩面ABCD＝AB，
∴CP⊥面ABB1A1，∴CP⊥AA1，
同理可得，CQ⊥AA1，
∵CP∩CQ＝C，CP、CQ⊂平面ABCD，
∴AA1⊥面ABCD．
（2）解：设MN∩AD＝F，连接EF，
∵F∈MN，MN⊂平面EMN，
∴F∈平面EMN，即EF⊂平面EMN，
同理EF⊂平面ADD1A1，
∴直线EF即为直线l，
∵AD∥BC，∴△MNC∽△FND，
∴DF＝1，
以A为原点，AB，AD，AA1所在直线分别为x，y，z轴建立如图所示的空间直角坐标系，
则B1（2，0，2），C（2，2，0），E（0，0，1），F（0，3，0），
∴＝（0，2，﹣2），＝（0，3，﹣1），
∴cs＜，＞＝＝＝，
∴直线l与B1C所成角的余弦值为．
21．（12分）已知双曲线E：﹣＝1（a＞0，b＞0）过点D（3，1），且该双曲线的虚轴端点与两顶点A1，A2的张角为120°．
（1）求双曲线E的方程；
（2）过点B（0，4）的直线1与双曲线E左支相交于点M，N，直线DM，DN与y轴相交于P，Q两点，求|BP|+|BQ|的取值范围．
【分析】（1）由已知可得，结合a2+b2＝c2，解得a，b即可；
（2）设直线方程y＝kx+4，M（x1，y1），N（x2，y2），由直线DM的方程和直线DN的方程可得P，Q的坐标，|BP|+||BQ|＝4﹣yM+4﹣yN＝6+＝6+3×，联立直线与双曲线方程，利用韦达定理即可求解．
【解答】解：（1）由已知可得，结合a2+b2＝c2，解得，
故双曲线E的方程；．
（2）设直线方程y＝kx+4，M（x1，y1），N（x2，y2），
直线DM的方程为y＝﹣1＝（x﹣3），可得P（0，1﹣），
直线DN的方程为y﹣1＝（x﹣3），可得Q（0，1﹣），
联立，消去y，整理可得（1﹣3k2）x2﹣24kx﹣54＝0，
则，可得，
|BP|+||BQ|＝4﹣yM+4﹣yN＝6+
＝6+3×
＝6+3×
＝6+3×
＝＝＝8﹣，
又，∴3k+5
∴|BP|+|BQ|的取值范围是（，18﹣6）．
22．（12分）已知函数f（x）＝（x﹣1）（aex﹣1）在x＝1处的切线方程为y＝（e﹣1）（x﹣1）．
（1）求a的值；
（2）若方程f（x）＝b有两个不同实根x1、x2，证明：．
【分析】（1）求出函数的导数，计算f′（1），得到关于a的方程，解出即可；
（2）根据函数的单调性分别求出以及x1≥﹣b，证明结论成立即可．
【解答】解：（1）∵f'（x）＝aex﹣1+（x﹣1）⋅aex，
∴k＝f'（1）＝ae﹣1＝e﹣1，∴a＝1；
（2）证明：∵f'（x）＝xex﹣1＝0有唯一实根x0∈（0，1），
x∈（﹣∞，x0）时，f'（x）＜0，f（x）递减，
x∈（x0，+∞）时，f'（x）＞0，f（x）递增，
故两根分别在（﹣∞，x0）与（x0，+∞）内，不妨设x1＜x2，
设g（x）＝f（x）﹣（e﹣1）（x﹣1），x∈（x0，+∞），
则g'（x）＝x⋅ex﹣e，x∈（x0，1）时，g'（x）＜0，g（x）递减，
x∈（1，+∞）时，g'（x）＞0，g（x）递增，
∴g（x）有最小值g（1）＝0，即f（x）≥（e﹣1）（x﹣1）恒成立，
b＝f（x2）≥（e﹣1）（x2﹣1），∴，
又因为函数f（x）在x＝0处的切线方程为y＝﹣x，
同上可证得f（x）≥﹣x恒成立，
b＝f（x1）≥﹣x1，∴x1≥﹣b，
于是．
x
1
2
3
4
y
32
48
72
88
不使用手机
使用手机
合计
学习成绩优秀人数
a
12
学习成绩不优秀人数
b
26
合计
P（K2≥k0）
0.10
0.05
0.01
0.005
0.001
k0
2.706
3.841
6.635
7.879
10.828
x
1
2
3
4
y
32
48
72
88
不使用手机
使用手机
合计
学习成绩优秀人数
a
12
学习成绩不优秀人数
b
26
合计
P（K2≥k0）
0.10
0.05
0.01
0.005
0.001
k0
2.706
3.841
6.635
7.879
10.828
不使用手机
使用手机
合计
学习成绩优秀人数
28
12
40
学习成绩不优秀人数
14
26
40
合计
42
38
80
X
0
1
2
3
P