2020-2021学年陕西省榆林市高一（上）12月月考数学试卷北师大版

展开

这是一份2020-2021学年陕西省榆林市高一（上）12月月考数学试卷北师大版，共9页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。

1. 已知A=x|x>−2， B=x|−3A.x|x>−3B.x|x<2C.RD.x|−2
2. 下列说法中正确的是( )
A.平行于同一平面的两条直线平行
B.垂直于同一直线的两个平面垂直
C.垂直于同一平面的两条直线平行
D.垂直于同一直线的两条直线平行

3. 下列命题中错误的是( )
A.如果α⊥β，那么α内所有直线都垂直于平面β
B.如果α⊥β，那么α内一定存在直线平行于平面β
C.如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β
D.如果α⊥γ，β⊥γ，α∩β=l，那么l⊥γ

4. 若a=0.50.7，b=0.70.5， c=ln23，则( )
A.c>b>aB.c>a>bC.a>b>cD.b>a>c

5. 在空间中，下列命题正确的是( )
A.若三条直线两两相交，则这三条直线确定一个平面
B.若直线m与平面α内的一条直线平行，则m//α
C.若a//α，a⊂β，α∩β=b，则a//b
D.若a//α，a//β，α∩β=l，则a与l相交

6. 设平面α // 平面β，A，C∈α，B，D∈β，直线AB与CD交于点S，且点S位于平面α，β之间，AS=8，BS=6，CS=12，则SD=( )
A.3B.9C.18D.10

7. 正方体的内切球和外接球的半径之比为( )
A.3:1B.3:2C.3:3D.2:3

8. 已知△ABC是边长为2a的正三角形，那么它的斜二测直观图的面积为( )
A.32a2B.34a2C.64a2D.6a2

9. 若正方体的棱长为2，则以该正方体各个面的中心为顶点的多面体的体积为( )
A.26B.23C.33D.23

10. 在空间四边形ABCD中，AD=BC=2，E，F分别是AB，CD的中点，EF=2，求AD与BC所成角的大小( )

A.30∘B.45∘C.60∘D.90∘

11. 如图，在多面体ABCDEF中，已知平面ABCD是边长为3的正方形，EF // AB，EF=32，且EF与平面ABCD的距离为2，则该多面体的体积为( )

A.92B.5C.6D.152
二、多选题

设函数fx=ln|3x+1|−ln|3x−1|，则fx( )
A.是偶函数，且在−13,13上单调递增
B.是偶函数，且在−∞,−13上单调递增
C.是奇函数，且在−13,13上单调递增
D.是奇函数，且在−∞,−13上单调递减
三、填空题

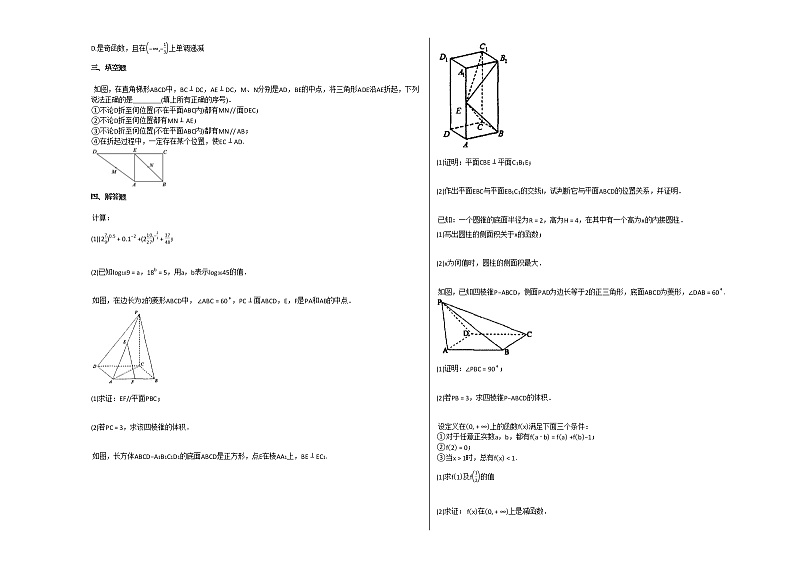
如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M、N分别是AD，BE的中点，将三角形ADE沿AE折起，下列说法正确的是________(填上所有正确的序号)．
①不论D折至何位置(不在平面ABC内)都有MN // 面DEC；
②不论D折至何位置都有MN⊥AE；
③不论D折至何位置(不在平面ABC内)都有MN // AB；
④在折起过程中，一定存在某个位置，使EC⊥AD.

四、解答题

计算：
(1)(279)0.5+0.1−2+(21027)−23+3748；

(2)已知lg189=a，18b=5，用a，b表示lg3645的值．

如图，在边长为2的菱形ABCD中， ∠ABC=60∘，PC⊥面ABCD，E，F是PA和AB的中点．

(1)求证：EF//平面PBC；

(2)若PC=3，求该四棱锥的体积．

如图，长方体ABCD−A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.

(1)证明：平面CBE⊥平面C1B1E；

(2)作出平面EBC与平面EB1C1的交线l，试判断它与平面ABCD的位置关系，并证明．

已知：一个圆锥的底面半径为R=2，高为H=4，在其中有一个高为x的内接圆柱．
(1)写出圆柱的侧面积关于x的函数；

(2)x为何值时，圆柱的侧面积最大．

如图，已知四棱锥P−ABCD，侧面PAD为边长等于2的正三角形，底面ABCD为菱形，∠DAB=60∘.

(1)证明：∠PBC=90∘；

(2)若PB=3，求四棱锥P−ABCD的体积．

设定义在0,+∞上的函数fx满足下面三个条件：
①对于任意正实数a，b，都有fa⋅b=fa+fb−1；
②f2=0；
③当x>1时，总有fx<1.
(1)求f1及f12的值

(2)求证： fx在0,+∞上是减函数．
参考答案与试题解析
2020-2021学年陕西省榆林市高一（上）12月月考数学试卷
一、选择题
1.
【答案】
D
【考点】
交集及其运算
【解析】
直接利用交集运算求解即可.
【解答】
解：∵ A=x|x>−2， B=x|−3A∩B=x|−2故选D.
2.
【答案】
C
【考点】
平行公理
空间中直线与直线之间的位置关系
【解析】
对4个命题分别进行判断，即可得出结论．
【解答】
解：对于A，平行于同一平面的两条直线平行、相交或异面，不正确；
对于B，垂直于同一直线的两个平面平行，不正确；
对于C，垂直于同一平面的两条直线平行，正确；
对于D，垂直于同一直线的两条直线平行、相交或异面，不正确.
故选C．
3.
【答案】
A
【考点】
平面与平面垂直的性质
【解析】
如果α⊥β，则α内与两平面的交线平行的直线都平行于面β，进而可推断出A命题正确；α内与两平面的交线平行的直线都平行于面β，故可判断出B命题错误；根据平面与平面垂直的判定定理可知C命题正确；根据两个平面垂直的性质推断出D命题正确．
【解答】
解：A，平面α内与两平面的交线平行的直线都平行于平面β，故A命题错误；
B，如果α⊥β，则α内与两平面的交线平行的直线都平行于面β，故B命题正确；
C，根据平面与平面垂直的判定定理可知，如果直线l⊥平面β，则直线l所在的平面α一定垂直于平面β，故C命题正确；
D，根据两个平面垂直的性质推断出，如果α⊥γ，β⊥γ，α∩β=l，那么l⊥γ，故D命题正确．
故选A.
4.
【答案】
D
【考点】
指数式、对数式的综合比较
【解析】
先求出c的范围，再利用指数函数和幂函数的单调性比较a，b，即可得到答案.
【解答】
解：∵ c=ln230∴ b>a>c.
故选D.
5.
【答案】
C
【考点】
空间中直线与直线之间的位置关系
空间中平面与平面之间的位置关系
直线与平面平行的性质
平行公理
【解析】
A，B，D可通过反例知命题为假命题，而C由线面平行的性质可知为真命题．
【解答】
解：A，三棱锥的三条侧棱两两相交，但不能确定一个平面，故A错误；
B，若直线m与平面α内的一条直线平行，则m//α或m⊂α，故B错误；
C，由线面平行的性质可知C正确；
D，若a//α，a//β，α∩β=l，则a与l平行，故D错误.
故选C.
6.
【答案】
B
【考点】
平面与平面平行的性质
两条直线平行的判定
平行线分线段成比例定理
【解析】
根据题意做出符合题意的图形，然后根据图形再结合线面平行的性质定理能求出SD的值．
【解答】
解：根据题意做出如下图形：
∵ AB，CD交于S点，设△ASC所在平面为n，
于是n交α于AC，交β于DB.
∵ α，β平行，
∴ AC // DB，
∴ △ASC∼△BSD，
∴ ASSB=CSSD.
∵ AS=8，BS=6，CS=12，
∴ 86=12SD，
解得SD=9．
故选B．
7.
【答案】
C
【考点】
球内接多面体
多面体的内切球问题
【解析】
此题暂无解析
【解答】
解：正方体的棱长是内切球的直径，正方体的对角线是外接球的直径，
设棱长是a，内切球的半径为r1，外接球的半径为r2，
则a=2r1，r1=a2，
又3a=2r2，r2=32a，
∴ r1:r2=1:3=3:3．
故选C．
8.
【答案】
C
【考点】
斜二测画法画直观图
【解析】
求出三角形的面积，利用平面图形的面积是直观图面积的2 2倍，求出直观图的面积即可．
【解答】
解：由三角形ABC是边长为2a的正三角形，三角形的面积为：34×(2a)2=3a2.
因为平面图形的面积与直观图的面积的比是2 2，
所以它的斜二测直观图的面积是：3a222=64a2．
故选C．
9.
【答案】
B
【考点】
柱体、锥体、台体的体积计算
【解析】
此题暂无解析
【解答】
解：由题意，以正方体各个面的中心为顶点的凸多面体是正八面体（即由两个同底等高的正四棱锥组成），所有棱长均为1，其中每个正四棱锥的高均为22，
故正八面体的体积V=2V正四棱锥=2×13×12×22=23．
故选B．
10.
【答案】
D
【考点】
异面直线及其所成的角
【解析】
利用异面直线所成角的定义求AD与BC所成角的．
【解答】
解：取AC的中点H，连结HE，HF.
因为E，F分别是AB，CD的中点，
所以HE // BC，HE=12BC=1，
HF // AD，HF=12AD=1，
所以HE与HF所成的角即为AD与BC所成的角．
在三角形EFH中，HF=1，HE=1，EF=2，
所以三角形EHF为直角三角形，
所以HE⊥HF，
即AD与BC所成角的大小为90∘．
故选D．
11.
【答案】
D
【考点】
柱体、锥体、台体的体积计算
【解析】
由已知中多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF与面AC的距离为2，我们易求出四棱锥E−ABCD的体积，然后根据整个几何体大于部分几何体的体积，分析已知中的四个答案，利用排除法，得到答案．
【解答】
解：分别取AB，CD的中点G，H连EG，GH，EH，
把该多面体分割成一个四棱锥与一个三棱柱，如图，
可求得四棱锥的体积为13×3×32×2=3，
三棱柱的体积为12×3×2×32=92，
整个多面体的体积为3+92=152．
故选D.
二、多选题
【答案】
C,D
【考点】
复合函数的单调性
函数奇偶性的判断
【解析】
结合奇偶性的定义检验f(−x)与f(x)的关系，然后结合导数可研究函数的单调性，可求．
【解答】
解：对于AB，f(x)的定义域为{x|3x+1≠0且3x−1≠0}，即−∞,−13∪−13,13∪13,+∞，定义域关于原点对称.
由于f(x)=ln|3x+1|−ln|3x−1|，
f(−x)=ln|−3x+1|−ln|−3x−1|
=ln|3x−1|−ln|3x+1|
=−f(x)，
故f(x)为奇函数，故AB错误；
对于C，当x∈−13,13时，
f(x)=ln(3x+1)−ln(1−3x)
=ln3x+11−3x
=ln(21−3x−1).
由于21−3x单调递增，故f(x)单调递增，故C正确；
对于D，当x∈(−∞,−13)时，
f(x)=ln(−1−3x)−ln(1−3x)
=ln−1−3x1−3x
=ln(1+−21−3x)
由于−21−3x单调递减，故f(x)单调递减，故D正确.
故选CD．
三、填空题
【答案】
①②④
【考点】
空间中直线与平面之间的位置关系
直线与平面平行的判定
【解析】
对于说法①，利用线面平行的判定定理，只需证MN平行于平面DEC内的直线DC即可；
对于说法②，由于MN // DC，要证明MN⊥AE，只需证明AE⊥CD，可转化为证AE⊥平面DEC，由AE⊥EC及AE⊥DE得证．
对于说法③，假设MN // AB，利用平行公理4逐步推导，得出矛盾，即可判断其正误．
【解答】
解：①在直角梯形ABCD中，由BC⊥DC，AE⊥DC，知四边形ABCE为矩形．
连结AC，
∵ N为BE中点，
∴ AC过点N．
当D折至某一位置时，如图所示，
连结MN，
∵ MN为△DAC的中位线，
∴ MN // DC，
由MN⊄平面DEC，DC⊂平面DEC，得MN // 平面DEC．
所以说法①正确．
②∵ AE⊥EC，AE⊥DE，EC∩DE=E，
∴ AE⊥平面DEC，又DC⊂平面DEC，
∴ AE⊥DC．
由①知，MN // DC，∴ MN⊥AE．
所以说法②正确．
③假设MN // AB，由MN // DC知，DC // AB，又CE // AB，得CE // CD，这与CE∩CD=C相矛盾，
所以假设不成立，即说法③错误．
④若EC⊥AD成立，∵EC⊥AE，AE∩AD=A，∴EC⊥平面AED，又CE⊂平面ABCE，故当平面ADE⊥平面ABCE时，EC⊥AD，故④正确.
故答案为：①②④．
四、解答题
【答案】
解：(1)原式=(53)2+102+3(34)6+3748
=53+100+916+3748
=103.
(2)∵ 18b=5，
∴ b=lg185.
又lg189=a，
∴ lg3645=lg1845lg1836
=lg189+lg185lg183249
=a+blg18182−lg189
=a+b2−a．
【考点】
根式与分数指数幂的互化及其化简运算
对数的运算性质
指数式与对数式的互化
【解析】
化指数式为对数式求得b，把要表示的式子换成以18为底数的对数得答案．
【解答】
解：(1)原式=(53)2+102+3(34)6+3748
=53+100+916+3748
=103.
(2)∵ 18b=5，
∴ b=lg185.
又lg189=a，
∴ lg3645=lg1845lg1836
=lg189+lg185lg183249
=a+blg18182−lg189
=a+b2−a．
【答案】
(1)∵ 证明∵ E，F分别为PA，PB的中点，
∴ 在△APB中，EF为中位线，
∴ EF//__12PB．
又∵ EF∉面PBC，
∴ EF//面PBC．
(2)解：由题知S四边形ABCD=2×12×2×2×32=23，
∵ PC=3且PC⊥ 面ABCD，
∴ V=12×32×3=23．
【考点】
直线与平面平行的判定
柱体、锥体、台体的体积计算
【解析】

【解答】
(1)∵ 证明∵ E，F分别为PA，PB的中点，
∴ 在△APB中，EF为中位线，
∴ EF//__12PB．
又∵ EF∉面PBC，
∴ EF//面PBC．
(2)解：由题知S四边形ABCD=2×12×2×2×32=23，
∵ PC=3且PC⊥ 面ABCD，
∴ V=12×32×3=23．
【答案】
(1)证明：∵B1C1⊥面ABB1A1，
∴B1C1⊥BE.
又∵BE⊥EC1且EC1∩B1C1=C1，
∴BE⊥面B1C1E.
又∵BE⊂面BEC，
∴平面BEC⊥平面B1C1E．
(2)解：l//平面ABCD．理由如下：
∵面B1C1E∩面BCC1B1=B1C1，面BCE∩面BCC1B1=BC，且B1C1//BC，
又∵面B1C1E∩BCE=l，
∴l//BC.
又∵l⊄面ABCD且BC⊂面ABCD，
∴l//面ABCD．
【考点】
平面与平面垂直的判定
直线与平面平行的判定
【解析】

【解答】
(1)证明：∵B1C1⊥面ABB1A1，
∴B1C1⊥BE.
又∵BE⊥EC1且EC1∩B1C1=C1，
∴BE⊥面B1C1E.
又∵BE⊂面BEC，
∴平面BEC⊥平面B1C1E．
(2)解：l//平面ABCD．理由如下：
∵面B1C1E∩面BCC1B1=B1C1，面BCE∩面BCC1B1=BC，且B1C1//BC，
又∵面B1C1E∩BCE=l，
∴l//BC.
又∵l⊄面ABCD且BC⊂面ABCD，
∴l//面ABCD．
【答案】
解：(1)设内接圆柱底面半径为r，
S圆柱侧=2πrx①，
∵ rR=H−xH，
∴ r=RH(H−x)=12(4−x)②，
将②代入①得S圆柱侧=2πx⋅12(4−x)
=π(−x2+4x)(0(2)∵ S圆柱侧=−π(x−2)2+4π，
∴ x=2时，圆柱的侧面积最大，最大为4π.
【考点】
棱柱、棱锥、棱台的侧面积和表面积
二次函数的性质
【解析】
（1）画出圆锥的轴截面，将空间问题转化为平面问题，然后根据相似三角形的性质和比例的性质，得出内接圆柱底面半径r与x关系式，利用由圆柱的侧面积公式，得到函数解析式，
（2）根据二次函数的性质易得到其最大值，及对应的x的值．
【解答】
解：(1)设内接圆柱底面半径为r，
S圆柱侧=2πrx①，
∵ rR=H−xH，
∴ r=RH(H−x)=12(4−x)②，
将②代入①得S圆柱侧=2πx⋅12(4−x)
=π(−x2+4x)(0(2)∵ S圆柱侧=−π(x−2)2+4π，
∴ x=2时，圆柱的侧面积最大，最大为4π.
【答案】
(1)证明：连结BD，取AD中点K，连结PK，BK.
∵PA=PD，
∴PK⊥AD.
又∵∠DAB=60∘且DA=AB，
∴△DAB为等边三角形，
∴AB=BD，
∴BK⊥AD.
又∵PK∩BK=K，
∴AD⊥面PBK，
∴AD⊥PB，
又∵AD//BC，
∴PB⊥BC，
∴ ∠PBC=90∘.
(2)解：∵AD⊥面PBK，∴面PBK⊥面ABCD.
作PQ⊥BK交BK延长线于Q，
则PQ⊥面ABCD.
∵PK=KB=3，且PB=3，
∴∠PKB=120∘，∠PBK=30∘，
∴∠KPQ=30∘，
∴PQ=3×32=32.
又∵菱形ABCD的面积S=2×3=23，
∴V四棱锥P−ABCD=13×23×32=3．
【考点】
两直线的夹角
两条直线垂直的判定
柱体、锥体、台体的体积计算
【解析】

【解答】
(1)证明：连结BD，取AD中点K，连结PK，BK.
∵PA=PD，
∴PK⊥AD.
又∵∠DAB=60∘且DA=AB，
∴△DAB为等边三角形，
∴AB=BD，
∴BK⊥AD.
又∵PK∩BK=K，
∴AD⊥面PBK，
∴AD⊥PB，
又∵AD//BC，
∴PB⊥BC，
∴ ∠PBC=90∘.
(2)解：∵AD⊥面PBK，∴面PBK⊥面ABCD.
作PQ⊥BK交BK延长线于Q，
则PQ⊥面ABCD.
∵PK=KB=3，且PB=3，
∴∠PKB=120∘，∠PBK=30∘，
∴∠KPQ=30∘，
∴PQ=3×32=32.
又∵菱形ABCD的面积S=2×3=23，
∴V四棱锥P−ABCD=13×23×32=3．
【答案】
(1)解：由题设得f2=f1+f2−1且f2=0，
所以f1=1.
又f1=f12⋅2=f12+f2−1且f1=1，
解得f12=2.
(2)证明：令01，
fx2−fx1=fx2⋅x1⋅1x1−fx1
=fx2x1⋅x1−f(x1)
=fx2x1+fx1−1−fx1=fx2x1−1.
因为当x>1时，f(x)<1，
所以fx2x1<1⇒fx2x1−1<0，
即fx2−fx1<0，
即fx2所以fx在0,+∞上为减函数.
【考点】
抽象函数及其应用
函数单调性的判断与证明
【解析】
利用∀a,b>0,fa⋅b=fa+fb−1对a,b赋值，得解.
利用函数的变形令01，
fx2−fx1=fx2⋅x1⋅1x1−fx1，
=fx2x1⋅x1−f(x1)，
=fx2x1+fx1−1−fx1=fx2x1−1，进而得解.
【解答】
(1)解：由题设得f2=f1+f2−1且f2=0，
所以f1=1.
又f1=f12⋅2=f12+f2−1且f1=1，
解得f12=2.
(2)证明：令01，
fx2−fx1=fx2⋅x1⋅1x1−fx1
=fx2x1⋅x1−f(x1)
=fx2x1+fx1−1−fx1=fx2x1−1.
因为当x>1时，f(x)<1，
所以fx2x1<1⇒fx2x1−1<0，
即fx2−fx1<0，
即fx2所以fx在0,+∞上为减函数.

2020-2021学年陕西省榆林市高一（上）12月月考数学试卷北师大版

更专业

更丰富

更便捷

真低价

欢迎来到教习网