2020-2021学年山西省晋中市高一（下）期末考试数学（文）试卷人教A版

这是一份2020-2021学年山西省晋中市高一（下）期末考试数学（文）试卷人教A版，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 已知复数z=1−2i，则zz¯+2i=（ ）
A.1−2iB.9+2iC.7−4iD.1+2i

2. 将圆锥的高缩短到原来的12，底面半径扩大到原来的2倍，则圆锥的体积（ ）
A.缩小到原来的一半B.缩小到原来的16
C.不变D.扩大到原来的2倍

3. 若一系列函数的解析式和值域相同，但其定义域不同，则称这些函数为“同族函数”，例如函数y=x2，x∈1,2与函数y=x2，x∈−2,−1即为“同族函数”．下面函数解析式中也能够被用来构造“同族函数”的是（ ）
A.y=sinxB.y=x3C.y=ex−e−xD.y=lnx

4. 甲、乙、丙三人独立地去译一个密码，分别译出的概率为12，14，18，则密码能被译出的概率是（ ）
A.120B.2132C.2164D.4364

5. 数据x1，x2，…，x9的平均数为4，标准差为2，则数据3x1+2，3x2+2，…，3x9+2的方差和平均数分别为（ ）
A.36，14B.14，36C.12，19D.4，12

6. 设λ为实数，已知向量m→=2,1−λ，n→=2,1．若m→⊥n→，则向量m→−n→与n→的夹角的余弦值为（ ）
A.−55B.−1010C.−12D.55

7. 若PAB=16，PA¯=13，PB=14，则事件A与B的关系是（ ）
A.互斥B.相互独立C.互为对立D.无法判断

8. 下图是函数fx=Asinωx+φA>0,ω>0的部分图象，则（ ）

A.函数y=fx的最小正周期为π2
B.直线x=5π12是函数y=fx图象的一条对称轴
C.点−π6,0是函数y=fx图象的一个对称中心
D.函数y=fx−π3为奇函数

9. 若定义在R上的奇函数fx在0,+∞上单调递减，且f−π2=0，则下列取值范围中的每个x都能使不等式fx+π2⋅csx≥0成立的是（ ）
A.−2π,−πB.−π,0
C.0,πD.x|x=kπ2,k∈Z

10. 如图，在直三棱柱ABC−A1B1C1中，AC=BC，AB=AA1，D是A1B1的中点，点F在BB1上，记B1F=λBF，若AB1⊥平面C1DF，则实数λ的值为（ ）

A.13B.12C.23D.1

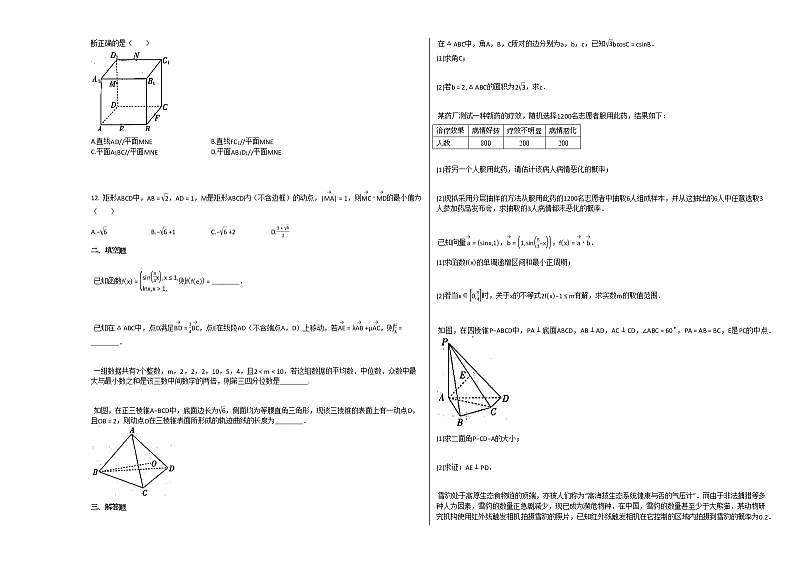
11. 如图所示，在正方体ABCD−A1B1C1D1 中，点E，F，M，N分别为棱AB，BC，DD1，D1C1上的中点，下列判断正确的是（ ）

A.直线AD//平面MNEB.直线FC1//平面MNE
C.平面A1BC//平面MNED.平面AB1D1//平面MNE

12. 矩形ABCD中，AB=2，AD=1，M是矩形ABCD内（不含边框）的动点，|MA→|=1，则MC→⋅MD→的最小值为（ ）
A.−6B.−6+1C.−6+2D.3+62
二、填空题

已知函数fx=sinπ4x,x≤1,lnx,x>1,则ffe=________．

已知在△ABC中，点D满足BD→=34BC→，点E在线段AD（不含端点A，D）上移动，若AE→=λAB→+μAC→，则μλ=________．

一组数据共有7个整数，m，2，2，2，10，5，4，且2
如图，在正三棱锥A−BCD中，底面边长为6，侧面均为等腰直角三角形，现该三棱锥的表面上有一动点O，且OB=2，则动点O在三棱锥表面所形成的轨迹曲线的长度为________．

三、解答题

在△ABC中，角A，B，C所对的边分别为a，b，c，已知3bcsC=csinB．
(1)求角C；

(2)若b=2,△ABC的面积为23，求c．

某药厂测试一种新药的疗效，随机选择1200名志愿者服用此药，结果如下：

(1)若另一个人服用此药，请估计该病人病情恶化的概率；

(2)现拟采用分层抽样的方法从服用此药的1200名志愿者中抽取6人组成样本，并从这抽出的6人中任意选取3人参加药品发布会，求抽取的3人病情都未恶化的概率．

已知向量a→=sinx,1，b→=1,sinπ3−x，fx=a→⋅b→．
(1)求函数fx的单调递增区间和最小正周期；

(2)若当x∈0,π4时，关于x的不等式2fx−1≤m有解，求实数m的取值范围．

如图，在四棱锥P−ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60∘，PA=AB=BC，E是PC的中点．

(1)求二面角P−CD−A的大小；

(2)求证：AE⊥PD．

雪豹处于高原生态食物链的顶端，亦被人们称为“高海拔生态系统健康与否的气压计”．而由于非法捕猎等多种人为因素，雪豹的数量正急剧减少，现已成为濒危物种．在中国，雪豹的数量甚至少于大熊猫．某动物研究机构使用红外线触发相机拍摄雪豹的照片，已知红外线触发相机在它控制的区域内拍摄到雪豹的概率为0.2．
(1)假定有5个红外线触发相机控制某个区域，求雪豹进入这个区域后未被拍摄到的概率；

(2)要使雪豹一旦进入这个区域后有0.9以上的概率被拍摄到，需至少布置几个红外线触发相机（lg2≈0.301）．

如图，已知四棱锥P−ABCD，△ABD为等边三角形，直线PC，DC，BC两两垂直，且PC=CD=BC=2，M为线段PA上的一点．

(1)若平面BDM⊥平面ABCD，求AM2；

(2)若三棱锥P−MBD的体积为四棱锥P−ABCD体积的12，求点M到平面ABCD的距离．
参考答案与试题解析
2020-2021学年山西省晋中市高一（下）期末考试数学（文）试卷
一、选择题
1.
【答案】
B
【考点】
复数代数形式的乘除运算
共轭复数
【解析】
无
【解答】
解：z¯=1+2i，
zz¯+2i=1−2i1+4i=9+2i．
故选B．
2.
【答案】
D
【考点】
柱体、锥体、台体的体积计算
【解析】
无
【解答】
解：设圆锥原来的高和底面半径分别为ℎ和r，圆锥原来体积为V1，变化后为V2，
V1=13πr2ℎ，V2=13π⋅2r2ℎ2=23πr2ℎ=2V1．
故选D．
3.
【答案】
A
【考点】
函数的值域及其求法
函数的定义域及其求法
函数新定义问题
【解析】
无
【解答】
解：y=x3，y=ex−e−x，y=lnx在其定义域内都单调，y=sinx可构造同族函数，
例如y=sinx，x∈0,π和y=sinx，x∈0,π2．
故选A．
4.
【答案】
D
【考点】
相互独立事件的概率乘法公式
【解析】
无
【解答】
解：∵ 甲、乙、丙三人独立地去译一个密码，分别译出的概率为12、14、18，
∴ 此密码不能译出的概率为1−12×1−14×1−18=2164，
故此密码能被译出的概率P=1−2164=4364．
故选D．
5.
【答案】
A
【考点】
极差、方差与标准差
众数、中位数、平均数
【解析】
无
【解答】
解：数据x1、x2，⋯、x9的平均数为4，标准差为2，
所以数据x1、x2，…，x9的方差为4，平均数为4．
根据方差和平均数的性质可得3x1+2、3x2+2，⋯、3x9+2的方差为32×4=36，平均数为3×4+2=14．
故选A．
6.
【答案】
A
【考点】
平面向量的坐标运算
数量积表示两个向量的夹角
【解析】
无
【解答】
解：由m→⊥n→，可得5−λ=0，
解得λ=5，
所以m→−n→=0,−5.
又m→−n→⋅n→=0,−5⋅2,1=−5，
且|m→−n→|=5，|n→|=22+1=5，
所以cs⟨m→−n→,n→⟩=m→−n→⋅n→|m→−n→||n→|=−55×5=−55．
故选A．
7.
【答案】
B
【考点】
互斥事件与对立事件
相互独立事件
【解析】
无
【解答】
解：因为PA¯=13，
所以PA=23.
又PB=14，
所以事件A与事件B不对立.
又因为PAB=16，
所以PAB=PAPB，
所以事件A与B相互独立但不一定互斥．
故选B．
8.
【答案】
C
【考点】
正弦函数的周期性
正弦函数的对称性
正弦函数的奇偶性
由y=Asin（ωx+φ）的部分图象确定其解析式
【解析】
无
【解答】
解：A．根据图象得，A=2，T=4π3−π12=π，则选项A错误；
B．ω=2πT=2，
又fπ12=2sin2×π12+φ=2，
解得π6+φ=2kπ+π2，k∈Z
则φ=2kπ+π3，k∈Z，
即fx=2sin2x+π3，f5π12=2sin7π6=−1，
所以直线x=5π12不是函数y=fx图象的一条对称轴，则选项B错误；
C．f−π6=2sin0=0，
所以点−π6,0是函数y=fx图象的一个对称中心，则选项C正确；
D．fx−π3=2sin2x−π3+π3=2sin2x−π3不是奇函数，则选项D错误．
故选C．
9.
【答案】
B
【考点】
其他不等式的解法
奇偶性与单调性的综合
【解析】
无
【解答】
解：由题意可知，偶函数fx在0,+∞上单调递减，且f−π2=0，
则fx在−∞,0上单调递减，
所以可画出大致图像，
而fx+π2可看作fx的图像向左平移π2个单位，可在同一坐标系中作出图像，
当x∈−π,0时，满足fx+π2⋅csx≥0恒成立．
故选B．
10.
【答案】
D
【考点】
直线与平面垂直的性质
【解析】
无
【解答】
解：因为C1D⊥A1B1，C1D⊥AA1，
所以C1D⊥平面AA1B1B，即C1D⊥AB1.
作DF⊥AB1交BB1于点F，
此时AB1⊥平面C1DF.
在矩形A1B1BA中，AB=A1A，
所以四边形A1B1BA是正方形，
所以A1B⊥AB1，
所以DF//A1B.
又D为A1B1的中点，
所以F为BB1的中点，即BB1=2B1F，
所以B1F=BF．
故选D．
11.
【答案】
D
【考点】
平面与平面平行的判定
【解析】
无
【解答】
解：A．过点M，N，E的截面如图所示（H，I，J均为中点），
所以直线AD与其相交于H点，故A项错误；
B．直线FC1与直线IJ在平面BCC1B1必定相交，故B项错误；
C．直线A1B与直线EI相交，故平面A1BC与平面MNE不平行，故C项错误；
D．直线AB1//直线EI，直线AD1//直线MH，
所以平面AB1D1//平面MNE，故D项正确．
故选D．
12.
【答案】
C
【考点】
向量在几何中的应用
正弦函数的定义域和值域
三角函数的最值
【解析】
无
【解答】
解：记∠MAD=θ，则∠MAB=π2−θ，θ∈0,π2，
MC→⋅MD→=MA→+AD→+DC→⋅MA→+AD→
=|MA→|2+2MA→⋅AD→+MA→⋅DC→+DC→⋅AD→+AD→2
=2+2MA→⋅AD→+MA→⋅AB→
=2−2csθ+2csπ2+θ
=2−2csθ−2sinθ
=2−6sinθ+φ，其中tanφ=2，φ∈0,π2，
所以当tanθ=22,θ∈0,π2时，MC→⋅MD→取最小值2−6．
故选C．
二、填空题
【答案】
22
【考点】
分段函数的应用
函数的求值
【解析】
无
【解答】
解：f(f(e))=f1=22．
故答案为：22．
【答案】
3
【考点】
向量在几何中的应用
向量的线性运算性质及几何意义
【解析】
无
【解答】
解：如图，由题意得存在实数m，使得AE→=mAD→0又AD→=AB→+BD→=AB→+34BC→
=AB→+34AC→−AB→=14AB→+34AC→，
所以AE→=m14AB→+34AC→=m4AB→+3m4AC→，
所以λ=m4,μ=3m4.
所以μλ=3．
故答案为：3．
【答案】
5
【考点】
众数、中位数、平均数
【解析】
此题暂无解析
【解答】
解：这组数据的平均数为m+257，众数为2，
当4≤m<10时，中位数为4，则有2+m+257=8⇒m=17，舍掉；
当2该7个数从小到大排列是2，2，2，3，4,5,10.
因为数据个数为7，而且7×75%=5.25，
所以这组数据的第三四分位数为5．
故答案为：5．
【答案】
3π2
【考点】
弧长公式
棱锥的结构特征
【解析】
无
【解答】
解：如图，轨迹为曲线EFGH，
因为BH=2，AB=3，
则∠ABH=π6，∠CBH=π4−π6=π12，
EF=GH=π12×2=π6.
又AH=1，∠CAD=π2，
则HE=π2，GF=π3×2=2π3，
所以点O的轨迹长度为2×π6+π2+2π3=3π2．
故答案为：3π2．
三、解答题
【答案】
解：(1)由正弦定理可得3sinBcsC=sinCsinB.
因为sinB≠0，所以3csC=sinC，
所以tanC=3.
因为C∈0,π，所以C=π3．
(2)由(1)得C=π3.
因为S△ABC=12absinC=34ab=23，
所以ab=8.
因为b=2，所以a=4.
由余弦定理得，c2=a2+b2−2abcsC=16+4−8=12，
所以c=23．
【考点】
正弦定理
余弦定理
【解析】
此题暂无解析
【解答】
解：(1)由正弦定理可得3sinBcsC=sinCsinB.
因为sinB≠0，所以3csC=sinC，
所以tanC=3.
因为C∈0,π，所以C=π3．
(2)由(1)得C=π3.
因为S△ABC=12absinC=34ab=23，
所以ab=8.
因为b=2，所以a=4.
由余弦定理得，c2=a2+b2−2abcsC=16+4−8=12，
所以c=23．
【答案】
解：(1)由统计表可知在1200名志愿者中，服用药出现病情恶化的频率为2001200=16，
所以估计另一个人服用此药病情恶化的概率为16．
(2)采用分层抽样的方法，从病情好转的志愿者中抽4人，从疗效不明显及病情恶化的志愿者中各抽取1人组成6个人的样本．
将6人中病情恶化的1人用符号A代替，其余5人分别用1，2，3，4，5代替，
则从6人中任意抽取3人的基本事件表示如下：
A,1,2，A,1,3，A,1,4，A,1,5，A,2,3，
A,2,4，A,2,5，(A,3,4)，(A,3,5)，A,4,5，
2,3,4，2,3,5，2,4,5，3,4,5，1,2,3，
1,2,4，1,2,5，1,3,4，1,3,5，1,4,5，共20个基本事件．
其中没有抽到病情恶化的志愿者的基本事件为：
2,3,4，2,3,5，2,4,5，3,4,5，1,2,3，
1,2,4，1,2,5，1,3,4，1,3,5，1,4,5，共10个基本事件，
因此，抽取的3人中没有病情恶化的志愿者的概率为1020=12．
【考点】
用频率估计概率
列举法计算基本事件数及事件发生的概率
【解析】
无
无
【解答】
解：(1)由统计表可知在1200名志愿者中，服用药出现病情恶化的频率为2001200=16，
所以估计另一个人服用此药病情恶化的概率为16．
(2)采用分层抽样的方法，从病情好转的志愿者中抽4人，从疗效不明显及病情恶化的志愿者中各抽取1人组成6个人的样本．
将6人中病情恶化的1人用符号A代替，其余5人分别用1，2，3，4，5代替，
则从6人中任意抽取3人的基本事件表示如下：
A,1,2，A,1,3，A,1,4，A,1,5，A,2,3，
A,2,4，A,2,5，(A,3,4)，(A,3,5)，A,4,5，
2,3,4，2,3,5，2,4,5，3,4,5，1,2,3，
1,2,4，1,2,5，1,3,4，1,3,5，1,4,5，共20个基本事件．
其中没有抽到病情恶化的志愿者的基本事件为：
2,3,4，2,3,5，2,4,5，3,4,5，1,2,3，
1,2,4，1,2,5，1,3,4，1,3,5，1,4,5，共10个基本事件，
因此，抽取的3人中没有病情恶化的志愿者的概率为1020=12．
【答案】
解：(1)因为fx=a→⋅b→=sinx+sinπ3−x
=12sinx+32csx=sinx+π3，
所以函数fx的最小正周期T=2π．
因为函数y=sinx的单调增区间为−π2+2kπ,π2+2kπ,k∈Z，
所以−π2+2kπ≤x+π3≤π2+2kπ,k∈Z，
解得−5π6+2kπ≤x≤π6+2kπ,k∈Z，
所以函数fx的单调增区间为−5π6+2kπ,π6+2kπ,k∈Z．
(2)不等式2fx−1≤m有解，即m+12≥fxmin．
因为x∈0,π4，所以π3≤x+π3≤7π12.
又sin7π12=sin5π12>sinπ3，
故当x+π3=π3，即x=0时，fx取得最小值，且最小值为f0=32，
所以m≥3−1．
【考点】
正弦函数的单调性
三角函数中的恒等变换应用
正弦函数的定义域和值域
【解析】
此题暂无解析
【解答】
解：(1)因为fx=a→⋅b→=sinx+sinπ3−x
=12sinx+32csx=sinx+π3，
所以函数fx的最小正周期T=2π．
因为函数y=sinx的单调增区间为−π2+2kπ,π2+2kπ,k∈Z，
所以−π2+2kπ≤x+π3≤π2+2kπ,k∈Z，
解得−5π6+2kπ≤x≤π6+2kπ,k∈Z，
所以函数fx的单调增区间为−5π6+2kπ,π6+2kπ,k∈Z．
(2)不等式2fx−1≤m有解，即m+12≥fxmin．
因为x∈0,π4，所以π3≤x+π3≤7π12.
又sin7π12=sin5π12>sinπ3，
故当x+π3=π3，即x=0时，fx取得最小值，且最小值为f0=32，
所以m≥3−1．
【答案】
(1)解：因为PA⊥底面ABCD，CD⊂平面ABCD，
所以CD⊥PA.
因为CD⊥AC,PA∩AC=A，
所以CD⊥平面PAC，
所以CD⊥PC.
又AC⊥CD，
故∠PCA为二面角P−CD−A的平面角.
又PA=AB=BC=AC，
故二面角P−CD−A的大小为45∘．
(2)证明：由于AE⊂平面PAC，
所以AE⊥CD.
因为E是PC 的中点，所以AE⊥PC.
又PC∩CD=C，所以AE⊥平面PCD.
又PD⊂平面PCD，所以AE⊥PD．
【考点】
二面角的平面角及求法
两条直线垂直的判定
【解析】
此题暂无解析
【解答】
(1)解：因为PA⊥底面ABCD，CD⊂平面ABCD，
所以CD⊥PA.
因为CD⊥AC,PA∩AC=A，
所以CD⊥平面PAC，
所以CD⊥PC.
又AC⊥CD，
故∠PCA为二面角P−CD−A的平面角.
又PA=AB=BC=AC，
故二面角P−CD−A的大小为45∘．
(2)证明：由于AE⊂平面PAC，
所以AE⊥CD.
因为E是PC 的中点，所以AE⊥PC.
又PC∩CD=C，所以AE⊥平面PCD.
又PD⊂平面PCD，所以AE⊥PD．
【答案】
解：(1)雪豹被拍摄到的概率，即至少有1个红外线触发相机拍摄到雪豹的概率．
设雪豹被第k个红外线触发相机拍摄到的事件为Akk=1,2,3,4,5，
那么5个红外线触发相机都未拍摄到雪豹的事件为A1¯⋅A2¯⋅A3¯⋅A4¯⋅A5¯．
∵ 事件A1¯，A2¯，A3¯，A4¯，A5¯相互独立，
∴ 雪豹未被拍摄到的概率为
P(A1¯⋅A2¯⋅A3¯⋅A4¯⋅A5¯)
=P(A1¯)⋅P(A2¯)⋅P(A3¯)⋅P(A4¯)⋅P(A5¯)
=(1−0.2)5=455，
∴ 雪豹未被拍摄到的概率为452．
(2)设至少需要布置n个红外线触发相机才能有0.9以上的概率拍摄到雪豹，
由(1)可知，雪豹被拍摄到的概率为1−45n.
令1−45n≥0.9，
∴ 45n≤110，
两边取常用对数，得n≥11−3lg2≈10.3.
∵ n∈N∗，
∴ n=11，
∴ 至少需要布置11个红外线触发相机才能有0.9以上的概率拍摄到雪豹．
【考点】
相互独立事件的概率乘法公式
互斥事件的概率加法公式
【解析】
无
无
【解答】
解：(1)雪豹被拍摄到的概率，即至少有1个红外线触发相机拍摄到雪豹的概率．
设雪豹被第k个红外线触发相机拍摄到的事件为Akk=1,2,3,4,5，
那么5个红外线触发相机都未拍摄到雪豹的事件为A1¯⋅A2¯⋅A3¯⋅A4¯⋅A5¯．
∵ 事件A1¯，A2¯，A3¯，A4¯，A5¯相互独立，
∴ 雪豹未被拍摄到的概率为
P(A1¯⋅A2¯⋅A3¯⋅A4¯⋅A5¯)
=P(A1¯)⋅P(A2¯)⋅P(A3¯)⋅P(A4¯)⋅P(A5¯)
=(1−0.2)5=455，
∴ 雪豹未被拍摄到的概率为452．
(2)设至少需要布置n个红外线触发相机才能有0.9以上的概率拍摄到雪豹，
由(1)可知，雪豹被拍摄到的概率为1−45n.
令1−45n≥0.9，
∴ 45n≤110，
两边取常用对数，得n≥11−3lg2≈10.3.
∵ n∈N∗，
∴ n=11，
∴ 至少需要布置11个红外线触发相机才能有0.9以上的概率拍摄到雪豹．
【答案】
解：(1)连接AC交BD于点O.
易知AC为线段BD的垂直平分线，且AC为AP在平面ABCD上的投影，
所以MD=MB.
连接MO，则MO⊥BD.
又因为平面BDM⊥平面ABCD，平面BDM∩平面ABCD=BD，MO⊂平面MBD，
所以MO⊥平面ABCD.
又因为AO⊂平面ABCD，所以MO⊥AO.
因为CO=2，AO=6，AP2=AC2+PC2=12+43.
又因为AOAC=AMAP，即AM2=18−63．
(2)过点M作平面ABCD的垂线，垂足为O′，
VM−ABD=13×12×6×22×MO′=233⋅MO′，
VP−BCD=43，
VP−ABCD=13×12×22×2+6×2=43+13，
故VP−BCD+VM−ABDVP−ABCD=1−12，
解得MO′=1−33，
故点M到平面ABCD的距离为1−33．
【考点】
平面与平面垂直的性质
点、线、面间的距离计算
【解析】
此题暂无解析
【解答】
解：(1)连接AC交BD于点O.
易知AC为线段BD的垂直平分线，且AC为AP在平面ABCD上的投影，
所以MD=MB.
连接MO，则MO⊥BD.
又因为平面BDM⊥平面ABCD，平面BDM∩平面ABCD=BD，MO⊂平面MBD，
所以MO⊥平面ABCD.
又因为AO⊂平面ABCD，所以MO⊥AO.
因为CO=2，AO=6，AP2=AC2+PC2=12+43.
又因为AOAC=AMAP，即AM2=18−63．
(2)过点M作平面ABCD的垂线，垂足为O′，
VM−ABD=13×12×6×22×MO′=233⋅MO′，
VP−BCD=43，
VP−ABCD=13×12×22×2+6×2=43+13，
故VP−BCD+VM−ABDVP−ABCD=1−12，
解得MO′=1−33，
故点M到平面ABCD的距离为1−33．治疗效果
病情好转
疗效不明显
病情恶化
人数
800
200
200