
2021届云南省高三理数二模试卷及答案
展开 高三理数二模试卷
一、单项选择题
1.满足 的集合 的个数是〔 〕
A. 1 B. 2 C. 3 D. 4
2. 是虚数单位, ,那么复数 的共轭复数等于〔 〕
A. B. C. D.
3.在 的二项展开式中, 的系数是〔 〕
A. 3 B. 5 C. 7 D. 9
4.〔 〕
A. 2 B. C. -2 D. -5
5.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,那么该几何体的体积是〔 〕
A. B. C. D.
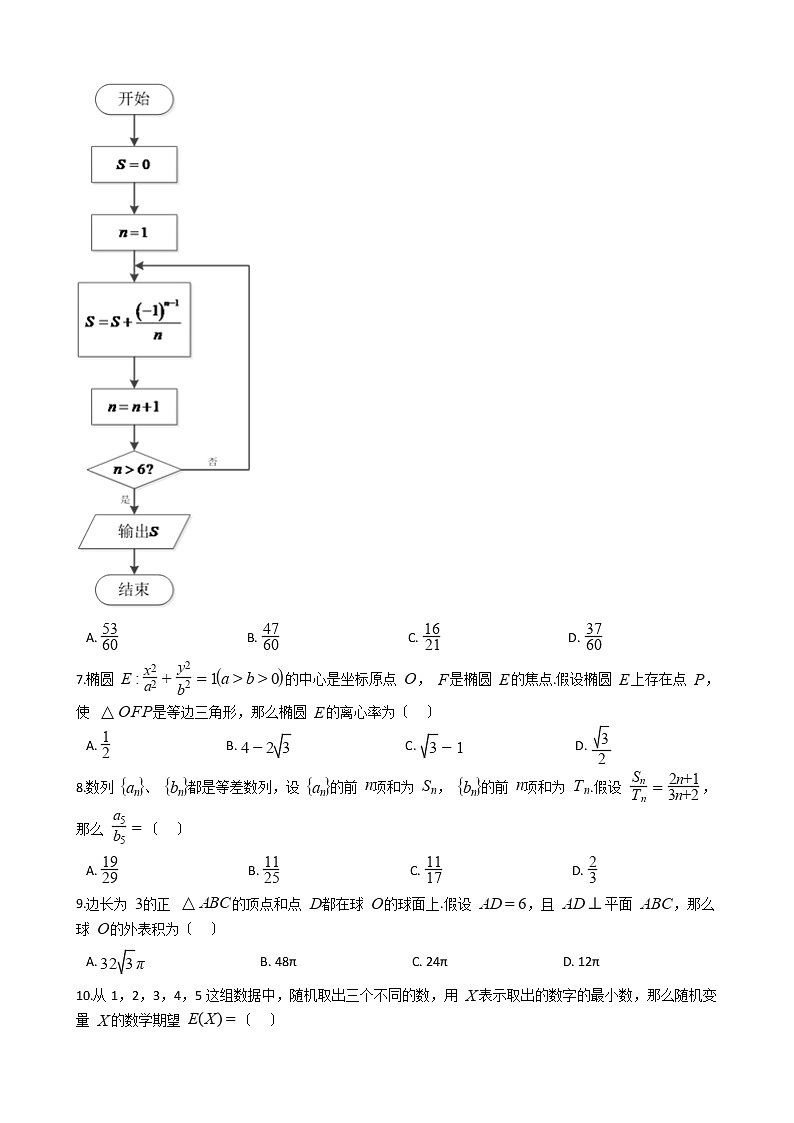
6.执行如图的程序框图,那么输出的结果是〔 〕
A. B. C. D.
7.椭圆 的中心是坐标原点 , 是椭圆 的焦点.假设椭圆 上存在点 ,使 是等边三角形,那么椭圆 的离心率为〔 〕
A. B. C. D.
8.数列 、 都是等差数列,设 的前 项和为 , 的前 项和为 .假设 ,那么 〔 〕
A. B. C. D.
9.边长为 的正 的顶点和点 都在球 的球面上.假设 ,且 平面 ,那么球 的外表积为〔 〕
A. B. 48π C. 24π D. 12π
10.从1,2,3,4,5这组数据中,随机取出三个不同的数,用 表示取出的数字的最小数,那么随机变量 的数学期望 〔 〕
A. B. C. D.
11.设数列 的前 项和为 , .假设 ,那么 〔 〕
A. 2 B. 4 C. 6 D. 8
12.函数 , ,且 在 上单调.设函数 ,且 的定义域为 ,那么 的所有零点之和等于〔 〕
A. 0 B. 4 C. 12 D. 16
二、填空题
13. , 都是平面向量.假设 , ,那么 ________.
14.圆 的圆心到双曲线 的渐近线的距离为________.
15.假设 , 满足约束条件 ,那么 的最大值为________.
16.函数 ,假设 ,且 ,设 ,那么 的取值范围为________.
三、解答题
17.的内角 、 、 的对边分别为 、 、 , .
〔1〕求 ;
〔2〕假设 ,求 面积 的最大值.
18.某公司为一所山区小学安装了价值2万元的一台饮用水净化设备,每年都要为这台设备支出保养维修费用,我们称之为设备年度保养维修费.下表是该公司第 年为这台设备支出的年度保养维修费 〔单位:千元〕的局部数据:
2
3
4
5
6
画出散点图如下:
通过计算得 与 的相关系数 .由散点图和相关系数 的值可知, 与 的线性相关程度很高.
附: , .
〔1〕建立 关于 的线性回归方程 ;
〔2〕假设设备年度保养维修费不超过1.93万元就称该设备当年状态正常,根据〔1〕得到的线性回归方程,估计这台设备有多少年状态正常?
19.如图,在三棱柱 中,四边形 是菱形, , , , 为棱 的中点.
〔1〕求证:平面 平面 ;
〔2〕假设 ,求二面角 的正弦值.
20. 是自然对数的底数, , .
〔1〕当 时,求证: 在 上单调递增;
〔2〕是否存在实数 ,对任何 ,都有 ?假设存在,求出 的所有值;假设不存在,请说明理由.
21.抛物线 的顶点在坐标原点,焦点在 轴的正半轴上,直线 经过抛物线 的焦点.
〔1〕求抛物线 的方程;
〔2〕假设直线 与抛物线 相交于 、 两点,过 、 两点分别作抛物线 的切线,两条切线相交于点 ,求 面积的最小值.
22.在平面直角坐标系 中,曲线 的参数方程为 〔 为参数〕.以坐标原点 为极点, 轴的正半轴为极轴建立极坐标系,点 的极坐标为 ,直线 的极坐标方程为 ,直线 过点 且与直线 平行.
〔1〕直接写出曲线 的普通方程和直线 的参数方程;
〔2〕设直线 与曲线 交于 、 两点.假设 是 与 的等比中项,求实数 的值.
23.函数 .
〔1〕假设 ,求实数 的取值范围;
〔2〕假设 ,且 ,求证: ,
答案解析局部
一、单项选择题
1.【解析】【解答】依题意得:
或 或 或
的个数有4个
故答案为:D
【分析】 由题意得, 再结合并集的定义即可解决.
2.【解析】【解答】由条件等式知: ,
∴ .
故答案为:A.
【分析】 把等式变形,再由复数代数形式的乘除运算化简,然后利用共轭复数的概念得答案.
3.【解析】【解答】由二项式通项 ,
∴当 时, ,那么 .
∴ 的系数是 .
故答案为:C.
【分析】 由题意利用二项式展开式的通项公式,求得 的二项展开式中,x的系数 .
4.【解析】【解答】
故答案为:B
【分析】 由两角差的正切公式,即可得解.
5.【解析】【解答】由三视图作出几何体的直观图如下:
由图可知:该几何体为三棱锥,且一条侧棱垂直于底面,底面是等腰直角三角形,
所以 ,
故答案为:C.
【分析】 利用三视图判断几何体的形状,利用三视图的数据求解几何体的体积即可.
6.【解析】【解答】执行程序框图的中的程序,如下所示:
第一次循环, , , 不满足;
第二次循环, , , 不满足;
第三次循环, , , 不满足;
第四次循环, , , 不满足;
第五次循环, , , 不满足;
第六次循环, , , 满足.
跳出循环体,输出 .
故答案为:D.
【分析】根据程序框图的循环结构,逐步进行验证,得出答案。
7.【解析】【解答】设点 为椭圆 上位于第一象限内的点,设 为椭圆 的左焦点,
因为 是等边三角形,那么 , ,
,所以, , ,
所以, ,
由椭圆的定义可得 ,
因此,椭圆E的离心率为 .
故答案为:C.
【分析】 求出P的坐标,代入椭圆方程,然后求解离心率即可.
8.【解析】【解答】∵ ,
∴ ,
故答案为:A
【分析】 利用等差数列的通项公式、求和公式及其性质即可得出,进而得出结论.
9.【解析】【解答】由题意知:球 为三棱锥 的外接球,
为边长为 的正三角形, 的外接圆半径 ,
又 平面 , , 球 的半径 ,
球 的外表积 .
故答案为:B.
【分析】 由题意画出图形,求出底面三角形 的外接圆的半径,进一步求出三棱锥外接球的半径,代入球的外表积公式得答案.
10.【解析】【解答】由题意知: 的可能值为1,2,3,而随机取3个数的取法有 种,
当 时,取法有 种,即 ;
当 时,取法有 种,即 ;
当 时,取法有 种,即 ;
∴ .
故答案为:A.
【分析】由题意知: 的可能值为1,2,3,由古典概型的概率求 , , , 进而求期望即可。
11.【解析】【解答】当 时,有 ,即 ,
当 时, ,即 ,
∴ 是首项为 ,公比为 的等比数列,那么 ,
∴ ,可得 .
故答案为:D.
【分析】 首先利用数列的递推关系式求出数列的通项公式,进一步利用数列的求和公式的应用求出结果.
12.【解析】【解答】由题设,知: ,而 ,
∴必有 ,又 在 上单调,即 ,
∴ ,那么 ,即有 ,又 ,
∴ ,所以 ,那么 ,
∴令 有 ,故判断 与 在 有几个交点及对应对称轴有哪几条即可,如以下图示:
∴共有6个零点且 ,即 .
故答案为:C.
【分析】先求出函数 的解析式,再根据图像判断 与 在 有几个交点及对应对称轴有哪几条即可。
二、填空题
13.【解析】【解答】因为 ,所以 .
故答案为:-3.
【分析】 求出向量 ,利用向量的数量积求解即可.
14.【解析】【解答】解:根据题意,圆 的圆心为 ,
双曲线的 的渐近线 ,即 ,
那么点 到直线 的距离 ,
即圆心到双曲线的渐近线的距离为 ;
故答案为: .
【分析】 求出圆的圆心,双曲线的渐近线方程,利用点到直线的距离公式求解即可.
15.【解析】【解答】由题设,可行域如下阴影局部所示,
∴当 与可行域有交点,在x轴的截距最大时, 的值最大.
当且仅当 过 时, .
故答案为:5.
【分析】 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
16.【解析】【解答】画出 图象如以下图所示,
,令 ,解得 ,
由 得 , ,且
所以 ,
结合二次函数的性质可知,当 时, 取得最大值为 ,当 时, 取得最小值为 .
所以 的取值范围是 .
故答案为:
【分析】画出图像,令 ,解得 , 由 得,且 , , 再根据二次函数的性质求出最值即可得出 的取值范围。
三、解答题
17.【解析】【分析】 〔1〕利用正弦定理将等式中的边化角,再结合三角形的内角和定理、两角和的正弦公式,即可得解;
〔2〕由余弦定理,得 , 结合根本不等式,推出 , 再由 , 得解.
18.【解析】【分析】〔1〕根据条件求出, 再根据公式可求出 即可得出 关于 的线性回归方程;
〔2〕 设这台设备有 年状态正常,由得 ,即 解不等式即可得出。
19.【解析】【分析】〔1〕 设 , 由四边形 是菱形, 为棱 的中点, 得 , ,再根据余弦定理可得 , 由勾股定理得出 , 根据面面垂直的判定定理可证得;
〔2〕 分别以射线 , , 为 轴, 轴, 轴的非负半轴,建立如以下图的空间直角坐标系 ,利用向量法求出二面角 的正弦值.
20.【解析】【分析】〔1〕对函数求导即可证出单调性;
〔2〕 由〔1〕知:当 时, 在 上单调递增, 当 时,设 ,那么 在 上是增函数,要使函数在 ,都有 ,那么实质是求函数 在 上的最小值是否满足条件, 设 , 那么 ,求出单调性,进而得出最值,即可得出结论。
21.【解析】【分析】〔1〕设出抛物线的方程,求出焦点坐标,带入直线进行求解即可;
〔2〕联立方程组,利用消元法转化为一元二次方程,根据根与系数之间的关系进行转化求解即可.
22.【解析】【分析】 〔1〕直接把曲线C的参数方程中的参数消去,可得其普通方程,化直线 的极坐标方程为直角坐标方程,化P的极坐标为直角坐标,结合直线 过点P且与直线 平行,可得直线 的参数方程;
〔2〕把直线 的参数方程代入曲线C的普通方程,化为关于t的一元二次方程,再由根与系数的关系及等比中项的性质、参数t的几何意义列式求解实数m的值.
23.【解析】【分析】〔1〕利用绝对值不等式的解法,分段求解即可得出实数 的取值范围;
〔2〕 ,利用根本不等式即可证得 。
2023高三三模【理数】试卷: 这是一份2023高三三模【理数】试卷,共4页。
2023榆林高三二模理数PDF含答案: 这是一份2023榆林高三二模理数PDF含答案,文件包含陕西省榆林市2022-2023学年高三二模理数答案pdf、陕西省榆林市2022-2023学年高三二模理数pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
南昌市2022届高三一模理数答案: 这是一份南昌市2022届高三一模理数答案,共4页。