
山东省青岛市市北区2020-2021学年七年级下学期期中数学试题(word版含答案)
展开山东省青岛市市北区2020-2021学年七年级下学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
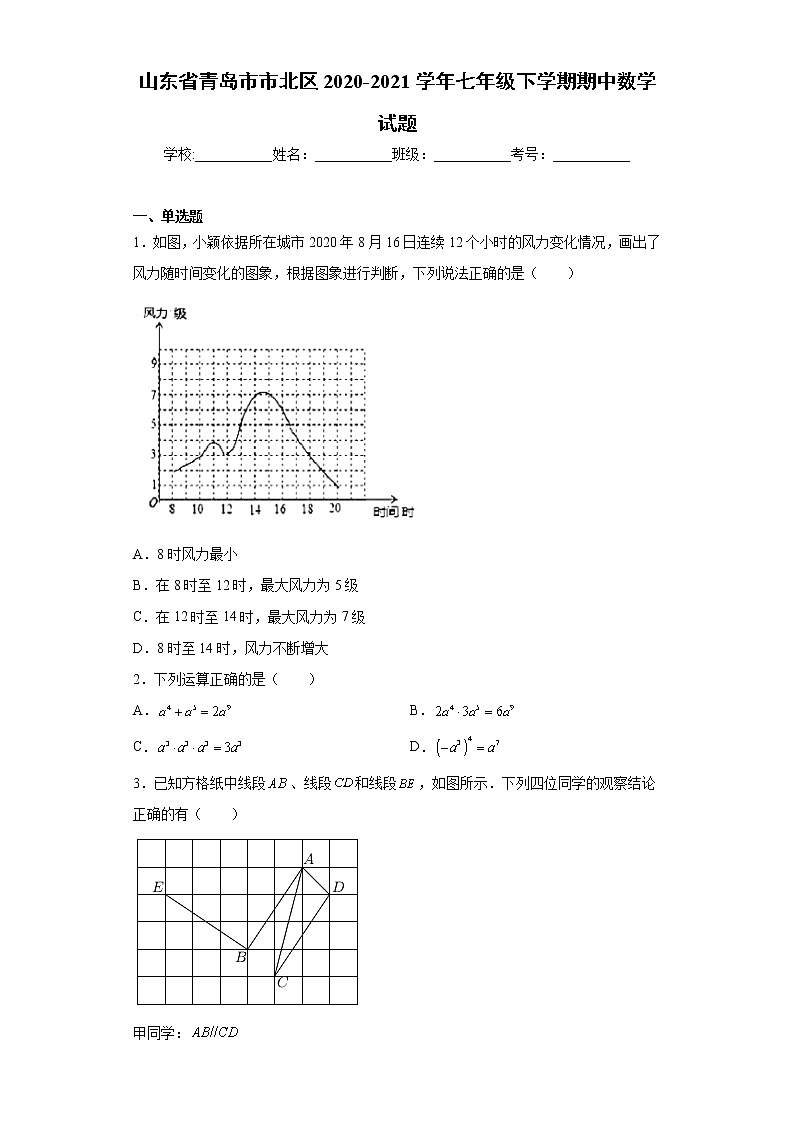
1.如图,小颖依据所在城市2020年8月16日连续12个小时的风力变化情况,画出了风力随时间变化的图象,根据图象进行判断,下列说法正确的是( )
A.8时风力最小
B.在8时至12时,最大风力为5级
C.在12时至14时,最大风力为7级
D.8时至14时,风力不断增大
2.下列运算正确的是( )
A. B.
C. D.
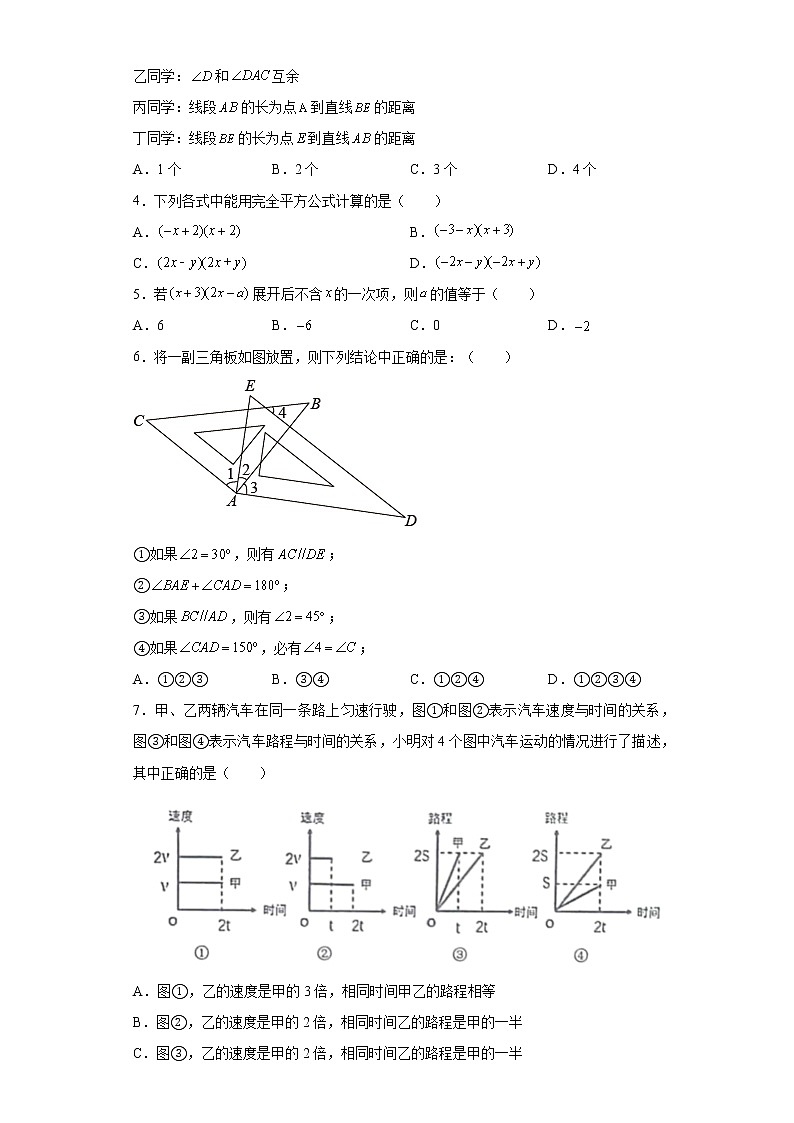
3.已知方格纸中线段、线段和线段,如图所示.下列四位同学的观察结论正确的有( )
甲同学:
乙同学:和互余
丙同学:线段的长为点到直线的距离
丁同学:线段的长为点到直线的距离
A.1个 B.2个 C.3个 D.4个
4.下列各式中能用完全平方公式计算的是( )
A. B.
C. D.
5.若展开后不含的一次项,则的值等于( )
A.6 B. C.0 D.
6.将一副三角板如图放置,则下列结论中正确的是:( )
①如果,则有;
②;
③如果,则有;
④如果,必有;
A.①②③ B.③④ C.①②④ D.①②③④
7.甲、乙两辆汽车在同一条路上匀速行驶,图①和图②表示汽车速度与时间的关系,图③和图④表示汽车路程与时间的关系,小明对4个图中汽车运动的情况进行了描述,其中正确的是( )
A.图①,乙的速度是甲的3倍,相同时间甲乙的路程相等
B.图②,乙的速度是甲的2倍,相同时间乙的路程是甲的一半
C.图③,乙的速度是甲的2倍,相同时间乙的路程是甲的一半
D.图④,乙的速度是甲的2倍,相同时间乙的路程是甲的2倍
8.将两个边分别为和的正方形拼在一起,、、三点在同一直线上,连接、,若两正方形的边长满足,,则阴影部分的面积为( )
A.95 B.85 C.90 D.100
二、填空题
9.______.
10.和互余,,是______度,的补角是______度.
11.新冠病毒的直径大约为90纳米,纳米是一个长度单位,1纳米米,用科学记数法表示病毒的直径为______米.
12.若是完全平方式,则_____.
13.某汽车生产厂家对其生产的一款汽车进行耗油量试验,在试验过程中,汽车一直匀速行驶,该汽车油箱中的余油量(升)与汽车的行驶时间(小时)之间的关系如表:
(小时) | 0 | 1 | 2 | 3 |
(升) | 120 | 112 | 104 | 96 |
则用关系式法表示因变量(升)与自变量(小时)之间的关系为______.
14.若,,则___________.
15.把一张长方形纸片沿翻折后,点、分别落在、的位置上,交于点,比多,则______度,______度.
16.在中国南宋数学家杨辉所著的《详解九章算法》中,出现了三角形形状的数列,又称为“杨辉三角形”.如图1,该三角形中的数据排列有着一定的规律,若将其中一组斜着的数列用字母,,,代替,如图2,计算,,的值,总结其规律,可得_____.
三、解答题
17.如图所示,在一块长方形的木板上,已知线段和外一点,请用尺规作图的方法作一条经过点的线段,使且与木板边缘交于点.
18.(1)
(2)
(3)(请利用公式进行简便运算)
(4)
19.已知.求:代数式的值.
20.填空:把下面的推理过程补充完整,并在括号内注明理由.
已知:如图,在中,于点,是上一点,且.
求证:.
证明:∵(已知)
∴______=_____(垂直定义)
∵(已知),
∴______(_______________).
∴(___________).
∴(________).
21.小红的物理老师说:“离地面越高,气温越低,高地面的高度每上升1千米,气温会下降6℃”,小红测得此时地面的气温为20℃.
(1)物理老师描述了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)根据物理老师的描述,请把温度的变化情况填入下表:
离地面高度(千米) | 0 | 1 | 2 | 3 | 4 |
温度(摄氏度) |
|
|
|
|
|
(3)在方格纸中,把离地面0千米、1千米、2千米、3千米、4千米高度的温度表示出来.
(4)请你预测离地面高度为5千米时,气温为多少摄氏度?
22.如图,已知直线,,,判断直线,直线的位置关系并说明理由.
23.周末,小明骑自行车从家出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程()与小明离家时间()的函数图象,已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若追上小明后,再过5分钟妈妈到达乙地,求从家到乙地的路程.
24.小张和小李玩猜数游戏,小张说:“你随便选三个一位数按这样的步骤去运算,①把第一个数乘5;②再加上10;③把所得结果乘以2;④加上第二个数;⑤把所得结果乘以10;⑥加上第三个数;只要你告诉我最后的得数,我就能知道你所想的三个一位数.”小李按照以上步骤试了几次,过程如下:
| 小李选定了1,2,3 | 小张选定了5,6,7 |
① | ||
② | ||
③ | ||
④ | ||
⑤ | ||
⑥ |
小张介绍了他的计算奥秘:将最后的得数减去200,所得的结果百位数就是第一个数,十位数就是第二个数,个位数就是第三个数.
探究一:证明小张想法的正确性
| 小李选定了,, |
① | |
② | |
③ | |
④ | |
⑤ | |
⑥ |
小张将最后的得数减去200:
,
所以结果百位数就是第一个数,十位数就是第二个数,个位数就是第三个数.小李听完后深受启发也设计了自己的运算程序,让小张随便选三个一位数按这样的步骤去运算:
①把第一个数乘5,再加上5;
②把第二个数乘20,再加上2;
③将①的运算结果与②的运算结果相乘,再加上第三个数;
④减去第一个数与第二个数乘积的100倍.
小李说:“只要小张告诉我最后的得数,我就能知道小张一开始所想的三个一位数。”
小李是如何知道的呢?请你模仿探究一的证明过程填写下表:
探究二:证明小李想法的正确性
| 设小张选定的三个数为,, |
① |
|
② |
|
③ |
|
④ |
|
请介绍小李的计算奥秘,描述:你是怎样由最后的得数,识别出最初选定的三个一位数的?
参考答案
1.C
【分析】
根据函数图像即可依次判断.
【详解】
由函数图象可得:20时风力最小,故A错误;
在8时至12时,最大风力为4级,故B错误;
在12时至14时,最大风力为7级,故C正确;
8时至14时,风力先增大,再减小,接着再增大,故D错误;
故选C.
【点睛】
此题主要考查由函数图象得到信息,解题的关键是熟知函数图象的特点及信息查找.
2.B
【分析】
根据幂的运算法则即可依次判断.
【详解】
A.不能计算,故错误;
B.,正确;
C.,故错误;
D.,故错误;
故选B.
【点睛】
此题主要考查幂的运算,解题的关键是熟知幂的运算公式的运用.
3.C
【分析】
连接AE、BC,然后根据平行线的定义和点到直线距离的定义可以得解.
【详解】
解:如图,连接AE、BC,
,
由图中可以看出,AB与CD方向一致,
∴AB∥CD,甲正确;
又从图中可以看出∠D 和 ∠DAC 不会互余,乙同学错误;
然后从图中不难得出AB⊥BE,
∴根据点到直线距离的定义,丙、丁同学正确,
故选C .
【点睛】
本题考查平行及垂直的判定、点到直线的距离定义.
4.B
【分析】
根据完全平方公式的特征即可判断.
【详解】
解:(A)不能用完全平方公式,
(B)原式==-,能用完全平方公式,
(C)不能用完全平方公式,
(D)不能用完全平方公式;
故选:B.
【点睛】
本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.
5.A
【分析】
先根据整式乘法去括号,再根据题意得6-a=0.
【详解】
∵=,展开后不含的一次项,
∴6-a=0
解得a=6
故选A
【点睛】
考核知识点:整式乘法.掌握整式乘法法则是关键.
6.D
【分析】
根据平行线的判定定理判断①;根据角的关系判断②即可;根据平行线的性质定理判断③;根据①的结论和平行线的性质定理判断④.
【详解】
解:∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴ACDE,①正确;
∵∠1+∠2=90°,∠2+∠3=90°,
即②∠BAE+∠CAD=∠1+∠2+∠2+∠3=90°+90°=180°,
故②正确;
∵BCAD,
∴∠1+∠2+∠3+∠C=180°,
又∵∠C=45°,∠1+∠2=90°,
∴∠3=45°,
∴∠2=90°−45°=45°,故③正确;
∵∠1=60°
∵∠E=60°,
∴∠1=∠E,
∴ACDE,
∴∠4=∠C,④正确.
故选:D.
【点睛】
本题考查的是平行线的性质和余角、补角的概念,掌握平行线的性质定理和判定定理是解题的关键.
7.D
【分析】
根据图像的信息,结合路程,速度,时间,三个要素的关系进行判断,即可.
【详解】
A. 图①,乙的速度是甲的2倍,都行驶了2t时间,
∴相同时间甲乙的路程相等是不准确的;
B. 图②,乙的速度是甲的2倍,相同时间乙的路程是甲的两倍,
∴相同时间乙的路程是甲的一半是错误的;
C. 图③,甲的速度是乙的2倍,
∴乙的速度是甲的2倍是错误的;
D. 图④,乙的速度是甲的2倍,相同时间乙的路程是甲的2倍,是正确的;
故选:D.
【点睛】
此题考查图像问题,关键是根据图像的信息,结合路程,速度,时间三个要素进行判断.
8.A
【分析】
利用两个正方形面积之和减去两个空白三角形,从而得到阴影部分面积,再根据已知条件求解即可.
【详解】
∵a+b=15,ab=35
∴= -2 ab=155
∴令阴影部分面积为S
S=-a(a-b)-
=(+ ab)
=95
故选A.
【点睛】
此题考查了完全平方公式的几何背景,整式的混合运算,熟练掌握运算法则是解本题的关键.
9.10
【分析】
根据负整数指数幂和零次幂的意义分别进行计算再求和即可得出答案.
【详解】
9+1=10
故答案为:10
【点睛】
本题主要考查了实数运算,正确化简各数是解题的关键.
10.34 146
【分析】
根据余角和补角的概念运算即可.
【详解】
解:∵和互余
∴
∴的补角
故答案为:34,146
【点睛】
本题主要考查了余角和补角的概念,熟悉掌握此概念列式运算是解题的关键.
11.
【分析】
结合题意,根据科学记数法和负整数指数幂的性质计算,即可得到答案.
【详解】
用科学记数法表示病毒的直径为:米
故答案为:.
【点睛】
本题考查了科学记数法和负整数指数幂的知识;解题的关键是熟练掌握负整数指数幂的性质,从而完成求解.
12.
【分析】
结合题意,根据完全平方式的性质计算,即可得到答案.
【详解】
∵是完全平方式
∴
∴
故答案为:.
【点睛】
本题考查了完全平方式的知识;解题的关键是熟练掌握完全平方式的性质,从而完成求解.
13.
【分析】
根据表格数据即可表示因变量y(升)与自变量t(小时)之间的关系.
【详解】
解:根据表格数据可知:
因变量y(升)与自变量t(小时)之间的关系为:,
故答案为:.
【点睛】
本题考查了函数的表示方法、常量与变量,解决本题的关键是函数的表示方法.
14.
【分析】
根据同底数幂除法逆运算及积的乘方逆运算解答.
【详解】
∵,,
∴,
故答案为:.
【点睛】
此题考查整式的运算公式:积的乘方计算及同底数幂除法计算,正确掌握计算公式并熟练应用是解题的关键.
15.55 55
【分析】
先根据平行线的性质得到=,再根据折叠的性质及平角的定义求出,进而得到,再根据平行线的性质得到.
【详解】
∵四边形是长方形
∴
∴=,
∵折叠,
∴=
又比多
∴比多
故=+
∵++=180°
∴+++=180°
解得=55°
∴=55°
∵
∴=55°
故答案为:55;55.
【点睛】
此题主要考查平行线的性质与角度求解,解题的关键是熟知两直线平行,内错角相等.
16.10000
【分析】
根据题意和图形中的数据,可知an=an−1+n,从而可以求得所求式子的值,本题得以解决.
【详解】
解:a1=1,
a2=1+2=3,
a3=3+3=6,
a4=6+4=10,
…,
an=an−1+n,
则a99+a100
=2a99+100
=2(a98+99)+100
=2(1+2+3+…+99)+100
=(1+99+2+98+…+99+1)+100
=9900+100
=10000.
故答案为:10000.
【点睛】
本题考查了规律型:图形的变化类,解决本题的关键是观察图形的变化寻找规律.
17.见详解
【分析】
根据同位角相等两直线平行作图即可.
【详解】
解:如图:
步骤:1,以A为圆心,以AQ的长为半径画弧线交AB于点E,
2,以C为圆心,以AQ的长为半径画弧线交AC于点P,
3, 以P为圆心,以QE的长为半径画弧线交于点F,
4,过点CF作AB的平行线交木板另一边于点D,
线段CD即为所求;
【点睛】
此题考查尺规作图,涉及平行线的判定定理,难度一般,注意利用判定定理是关键.
18.(1);(2);(3)4044;(4)
【分析】
(1)利用积的乘方,单项式与单项式的乘除计算法则求解即可;
(2)利用完全平方公式和平方差公式求解即可;
(3)利用完全平方公式和平方差公式求解即可;
(4)利用平方差公式求解即可.
【详解】
解:(1)
;
(2)
;
(3)
;
(4)
.
【点睛】
本题主要考查了平方差公式,完全平方公式,单项式与单项式的乘除法,积的乘方,解题的关键在于能够熟练掌握相关知识进行求解.
19.原式,3
【分析】
利用完全平方公式和平方差公式化简代数式,再把已知代数式转化代入运算即可.
【详解】
解:
原式
∵
∴
∴把代入得:
【点睛】
本题主要考查了代数式的运算,其中涉及到了完全平方和平方差的运算,熟悉掌握公式化简是解题的关键.
20.;9;;同角的余角相等;内错角相等,两直线平行;两直线平行,同旁内角互补
【分析】
根据垂直的定义、平行线的判定与性质即可求解.
【详解】
求证:.
证明:∵(已知)
∴=9(垂直定义)
∵(已知),
∴(同角的余角相等).
∴(内错角相等,两直线平行).
∴(两直线平行,同旁内角互补).
故答案为:;9;;同角的余角相等;内错角相等,两直线平行;两直线平行,同旁内角互补
【点睛】
此题考查了平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键.
21.(1)物理老师描述了离地面的高度与气温之间的关系,离地面的高度是自变量,气温是因变量;(2)20,14,8,2,;(3)见解析;(4)℃
【分析】
(1)从表格的数据易得上表反映的是温度和离地面高度之间的关系,从数据的对应的关系可知属于函数关系;
(2)根据题意即可计算求解;
(3)根据(2)所求即可表示出来;
(4)根据题中温度变化的规律即可求解.
【详解】
(1)上表反映了温度和离地面高度之间的关系,离地面高度是自变量,温度是因变量;
(2)∵离地面越高,气温越低,高地面的高度每上升1千米,气温会下降6℃”,小红测得此时地面的气温为20℃.
∴当离地面高度为0千米时,地面的气温为20℃;
当离地面高度为1千米时,地面的气温为20-6=14℃;
当离地面高度为2千米时,地面的气温为14-6=8℃;
当离地面高度为3千米时,地面的气温为8-6=2℃;
当离地面高度为4千米时,地面的气温为2-6=-4℃;
故答案为:20,14,8,2,;
(3)如图,把离地面0千米、1千米、2千米、3千米、4千米高度的温度表示出来如下.
(4)当离地面高度为5千米时,地面的气温为-4-6=-10℃.
【点睛】
本题考查了函数的表示表格形式的方法及其基本应用,明确函数的基本定义及读懂表格中数据是解题的关键.
22.,理由见解析
【分析】
m//n ,根据a//b ,可得出∠2+∠3=180°,再根据角度可得出∠3=∠1,即可得出结论.
【详解】
解:m//n ,证明如下:
如图:
∵a//b ,
∴∠2+∠3=180°,
∵∠1=70° , ∠2=110° ,
∴∠3=70°,
∴∠3=∠1,
∴m//n ;
【点睛】
此题考查平行线的性质与判定,主要涉及同位角和同旁内角,难度一般.
23.(1)20, 0.5(2),25;(3)30
【分析】
(1)由小明花骑行,从而可求解骑车的速度,利用图象可得在甲地游玩的时间,从而可得答案;
(2)利用小明的骑行时间乘以骑行的速度即可得到答案;
(3)利用妈妈的行驶时间乘以行驶速度即可得到答案.
【详解】
解:(1)小明骑车的速度为
在甲地游玩的时间为:
(2)由图象可得:小明从家出发小时后被妈妈追上,
此时离家
(3)妈妈的速度为:
从家到乙地的路程为:
【点睛】
本题考查的是从函数图象中获取信息,理解坐标含义,熟练路程,时间,速度关系是解题的关键.
24.,,,;将最后的得数减去10,所得百位数就是第二个数,十位数是第一个数,个位数是第三个数,证明见解析.
【分析】
根据题意即可写出对应的代数式,计算即可求解;根据最终得到的代数式的特点即可求解.
【详解】
设小张选定的三个数为,,
①把第一个数乘5,再加上5,即为;
②把第二个数乘20,再加上2,即为;
③将①的运算结果与②的运算结果相乘,再加上第三个数,即()()+=
100xy+10x+100y+z=;
④减去第一个数与第二个数乘积的100倍,即为-100xy=.
故填表如下:
| 设小张选定的三个数为,, |
① | |
② | |
③ | |
④ |
小李的计算奥秘:将最后的得数减去10,即-10=
∴所得百位数就是第二个数,十位数是第一个数,个位数是第三个数.
【点睛】
此题主要考查列代数式,整式的加减、乘法运算,解题的根据是根据题意写出代数式,再进行相应的求解.
山东省青岛市市北区2023-2024学年七年级下学期期中数学试题: 这是一份山东省青岛市市北区2023-2024学年七年级下学期期中数学试题,共8页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。
山东省青岛市市北区2023~2024学年下学期期中质量调研七年级数学试题: 这是一份山东省青岛市市北区2023~2024学年下学期期中质量调研七年级数学试题,共4页。
山东省青岛市市北区2022-2023学年七年级上学期期中数学试题: 这是一份山东省青岛市市北区2022-2023学年七年级上学期期中数学试题,共6页。












