安徽省滁州市南谯区2020-2021学年九年级上学期期末数学试卷（word版含答案）

2020-2021学年安徽省滁州市南谯区九年级（上）期末数学试卷

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的.

1．下列图案中，是中心对称图形的是（　　）

A． B． 

C． D．

2．对抛物线y＝﹣x2+4x﹣3而言，下列结论正确的是（　　）

A．开口向上 

B．与y轴的交点坐标是（0，3） 

C．与两坐标轴有两个交点 

D．顶点坐标是（2，1）

3．点P1（﹣1，y1），P2（3，y2），P3（5，y3）均在二次函数y＝﹣x2+2x+c的图象上，则y1，y2，y3的大小关系是（　　）

A．y1＝y2＞y3 B．y1＞y2＞y3 C．y3＞y2＞y1 D．y3＞y1＝y2

4．如图，在△ABC中，AB＝3，BC＝5.2，∠B＝60°，将△ABC绕点A逆时针旋转得到△ADE，若点B的对应点D恰好落在BC边上时，则CD的长为（　　）

A．0.8 B．2 C．2.2 D．2.8

5．如图，在直角坐标系中，△OAB的顶点为O（0，0），A（﹣6，4），B（﹣3，0）．以点O为位似中心，在第四象限内作与△OAB的位似比为的位似图形△OCD，则点C坐标为（　　）

A．（2，﹣1） B．（3，﹣2） C．（，﹣） D．（，﹣1）

6．如图，已知点A为反比例函数y＝（x＜0）的图象上一点，过点A作AB⊥y轴，垂足为B，若△OAB的面积为3，则k的值为（　　）

A．3 B．﹣3 C．6 D．﹣6

7．若ad＝bc（b≠d）且a，b，c，d均为正数，则下列结论不成立的是（　　）

A． B． 

C． D．

8．如图，AB是⊙O的直径，点C、D在⊙O上，且OC∥DB，连接AD、CD，若∠C＝28°，则∠A的大小为（　　）

A．30° B．28° C．24° D．34°

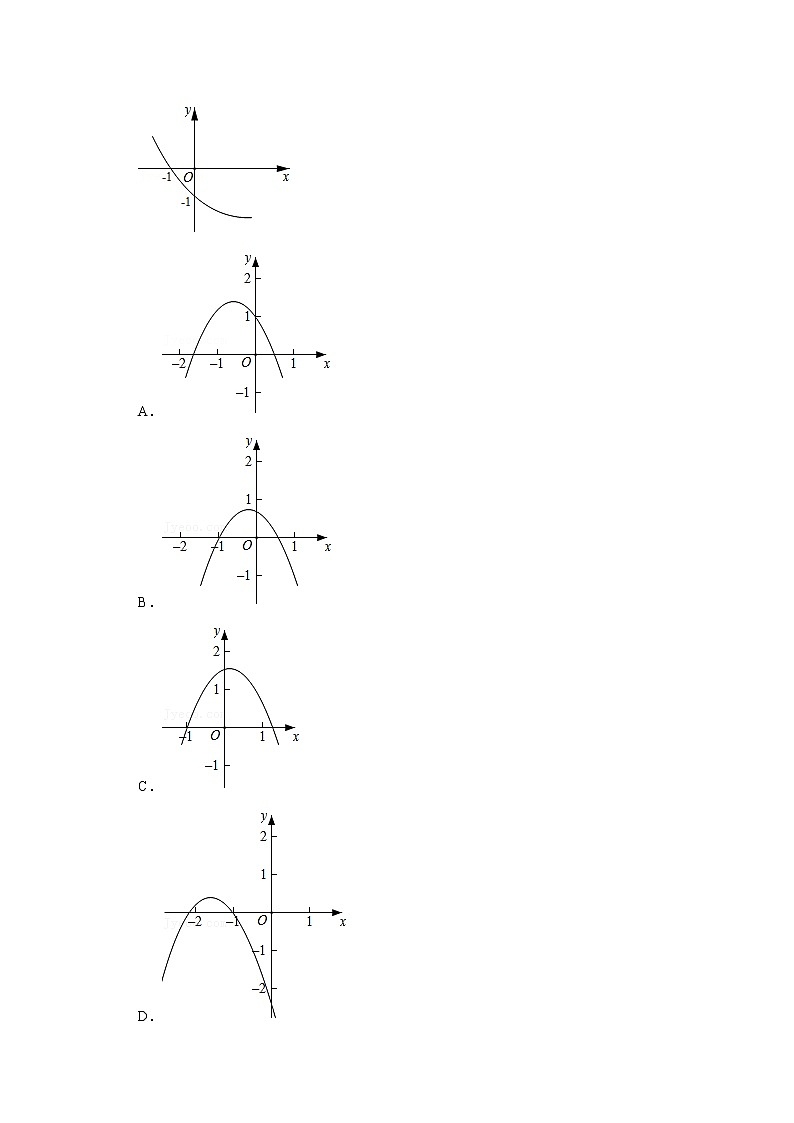
9．如图，抛物线y＝ax2+bx+c经过（﹣1，0）和（0，﹣1）两点，则抛物线y＝cx2+bx+a的图象大致为（　　）

A． 

B． 

C． 

D．

10．正方形ABCD中，AB＝4，P为对角线BD上一动点，F为射线AD上一点，若AP＝PF，则△APF的面积最大值为（　　）

A．8 B．6 C．4 D．2

二、填空题（本大题共4小题，每小题5分，满分20分）

11．（5分）抛物线y＝﹣（x+2）2的顶点坐标是　       　．

12．（5分）如图，若芭蕾舞者抬起的脚尖点C分线段AB近似于黄金分割（AC＜BC），已知AB＝160cm，BC的长约为　     　cm．（结果精确到0.1cm）

13．（5分）如图，在边长为1的小正方形网格中，点A、B、C均在格点上，则tanB的值为　              　．

14．（5分）如图，矩形ABCD中，AB＝6，AD＝8，点P是AB边上动点，把△ADP沿DP折叠得△A'DP，射线DA'交射线AB于点Q，

（1）当Q点和B点重合时，PQ长为　               　；

（2）当△A'DC为等腰三角形时，则DQ长为　               　．

三、（本大题共2小题，每小题8分，满分16分）

15．（8分）计算：2sin245°﹣6cos30°+3tan45°+4sin60°．

16．（8分）如图，二次函数y＝﹣+bx+c的图象经过A（2，0）、B（0，﹣4）两点．

（1）求这个二次函数的解析式；

（2）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．

四、（本大题共2小题，每小题8分，满分16分）

17．（8分）如图，一次函数y1＝kx+b的图象与反比例函数y2＝的图象交于A、B两点．

（1）利用图中的条件，求反比例函数和一次函数的解析式；

（2）根据图象直接写出使y1＜y2的自变量x取值范围．

18．（8分）如图，在网格图中（小正方形的边长为1），△ABC的三个顶点都在格点上．

（1）把△ABC沿着x轴向右平移6个单位得到△A1B1C1，请画出△A1B1C1；

（2）请以坐标系的原点O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2，使得△ABC与△A2B2C2的位似比为1：2；

（3）请直接写出△A2B2C2三个顶点的坐标．

五、（本大题共2小题，每小题10分，满分20分）

19．（10分）2020年6月23日，我国第55颗北斗卫星，即北斗全球卫星导航系统最后一颗组网卫星发射成功．北斗导航装备的不断更新，极大方便人们的出行．某中学从A地出发，组织学生利用导航到C地区进行研学活动，已知C地位于A地的正北方向，且距离A地24千米．由于A、C两地间是一块湿地，所以导航显示的路线是沿北偏东60°方向走到B地，再沿北偏西37°方向走一段距离才能到达C地，求A、B两地的距离（精确到1千米）．

（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.7，≈1.4，≈1.7）

20．（10分）已知：如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，E为直角边AC的中点，过D，E作直线交AB的延长线于F．

（1）若AB＝6，AC＝8，求BD长；

（2）求证：AB•AF＝AC•DF．

六、（本题满分12分）

21．（12分）如图，AB是⊙O的直径，点C，M为⊙O上两点，且C点为的中点，过C点的切线交射线BM、BA于点E、F．

（1）求证：BE⊥FE；

（2）若∠F＝30°，MB＝2，求的长度．

七、（本题满分12分）

22．（12分）如图，已知抛物线y1＝a（x﹣1）（x﹣5）和直线y2＝﹣ax﹣a（其中a＞0）相交于A，B两点，抛物线y1与x轴交于C，D两点，与y轴交于点G，直线y2与坐标轴交于E，F两点．

（1）若G的坐标为（0，5），求抛物线y1解析式和直线y2解析式；

（2）求证：直线y2＝﹣ax﹣a始终经过该抛物线y1的顶点；

（3）求的值．

八、（本题满分14分）

23．（14分）如图1，△ABC中，∠ACB＝90°，AC＝BC，E为△ABC的中线BD上的一点，将线段AE以E点为中心逆时针旋转90°得到线段EF，恰EF经过点C．

（1）若∠CAF＝α，则∠CBE＝　   　（用α的代数式表示）．

（2）如图2，过点C作CH∥AE，交AF于点H，连接BH交EF于点G，

①求证：AF＝BH；

②若CF＝2，求EG的长．

2020-2021学年安徽省滁州市南谯区九年级（上）期末数学试卷

参考答案与试题解析

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的.

1．下列图案中，是中心对称图形的是（　　）

A． B． 

C． D．

【分析】把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，据此可得结论．

【解答】解：A．是中心对称图形，故本选项符合题意；

B．不是中心对称图形，故本选项不合题意；

C．不是中心对称图形，故本选项不合题意；

D．不是中心对称图形，故本选项不合题意．

故选：A．

2．对抛物线y＝﹣x2+4x﹣3而言，下列结论正确的是（　　）

A．开口向上 

B．与y轴的交点坐标是（0，3） 

C．与两坐标轴有两个交点 

D．顶点坐标是（2，1）

【分析】根据Δ的符号，可判断图象与x轴的交点情况，根据二次项系数可判断开口方向，令函数式中x＝0，可求图象与y轴的交点坐标，利用配方法可求图象的顶点坐标．

【解答】解：A、二次项系数a＝﹣1＜0，抛物线开口向下，结论错误，不符合题意；

B、当x＝0时，y＝﹣3，抛物线与y轴交点坐标为（0，﹣3），结论错误，不符合题意；

C、Δ＝42﹣4×（﹣1）×（﹣3）＝4＞0，抛物线与x轴有两个交点，与y轴有1个交点，即与两坐标轴有3个交点，结论错误，不符合题意；

D、由y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1知，抛物线顶点坐标为（2，1），结论正确，符合题意；

故选：D．

3．点P1（﹣1，y1），P2（3，y2），P3（5，y3）均在二次函数y＝﹣x2+2x+c的图象上，则y1，y2，y3的大小关系是（　　）

A．y1＝y2＞y3 B．y1＞y2＞y3 C．y3＞y2＞y1 D．y3＞y1＝y2

【分析】先求出抛物线的对称轴方程，然后根据二次函数的性质，通过比较三个点到对称轴的距离大小可得到y1，y2，y3的大小关系．

【解答】解：二次函数y＝﹣x2+2x+c的图象的对称轴为直线x＝﹣＝1，

而P1（﹣1，y1）和P2（3，y2）到直线x＝1的距离都为2，P3（5，y3）到直线x＝1的距离为4，

所以y1＝y2＞y3．

故选：A．

4．如图，在△ABC中，AB＝3，BC＝5.2，∠B＝60°，将△ABC绕点A逆时针旋转得到△ADE，若点B的对应点D恰好落在BC边上时，则CD的长为（　　）

A．0.8 B．2 C．2.2 D．2.8

【分析】由旋转的性质可得AB＝AD＝3，可证△ABD是等边三角形，可得BD＝AB＝3，即可求解．

【解答】解：∵将△ABC绕点A逆时针旋转得到△ADE，

∴AB＝AD＝3，

∵∠B＝60°，

∴△ABD是等边三角形，

∴BD＝AB＝3，

∴CD＝BC﹣BD＝5.2﹣3＝2.2，

故选：C．

5．如图，在直角坐标系中，△OAB的顶点为O（0，0），A（﹣6，4），B（﹣3，0）．以点O为位似中心，在第四象限内作与△OAB的位似比为的位似图形△OCD，则点C坐标为（　　）

A．（2，﹣1） B．（3，﹣2） C．（，﹣） D．（，﹣1）

【分析】直接利用位似图形的性质得出对应点坐标与位似比的关系．

【解答】解：∵△OAB的顶点为O（0，0），A（﹣6，4），B（﹣3，0），以点O为位似中心，在第四象限内作与△OAB的位似比为的位似图形△OCD，

∴点C坐标为：[﹣6×（﹣），4×（﹣）]，即（3，﹣2）．

故选：B．

6．如图，已知点A为反比例函数y＝（x＜0）的图象上一点，过点A作AB⊥y轴，垂足为B，若△OAB的面积为3，则k的值为（　　）

A．3 B．﹣3 C．6 D．﹣6

【分析】再根据反比例函数的比例系数k的几何意义得到|k|＝2，然后去绝对值即可得到满足条件的k的值．

【解答】解：

∵AB⊥y轴，

∴S△OAB＝|k|，

∴|k|＝3，

∵k＜0，

∴k＝﹣6．

故选：D．

7．若ad＝bc（b≠d）且a，b，c，d均为正数，则下列结论不成立的是（　　）

A． B． 

C． D．

【分析】由四条线段a、b、c、d成比例，根据成比例线段的定义解答．

【解答】解：由ad＝bc（b≠d）且a，b，c，d均为正数，

可得：，故A正确；

∴，故B正确；

∴，故D正确；

不能得出，故C错误；

故选：C．

8．如图，AB是⊙O的直径，点C、D在⊙O上，且OC∥DB，连接AD、CD，若∠C＝28°，则∠A的大小为（　　）

A．30° B．28° C．24° D．34°

【分析】证明∠COB＝∠OBD＝56°，再证明∠ADB＝90°，即可求出∠DAB．

【解答】解：∵OC∥BD，

∴∠C＝∠CDB＝28°，

∴∠COB＝2∠CDB＝56°，

∴∠COB＝∠B＝56°，

∵AB是直径，

∴∠ADB＝90°，

∴∠DAB＝90°﹣56°＝34°，

故选：D．

9．如图，抛物线y＝ax2+bx+c经过（﹣1，0）和（0，﹣1）两点，则抛物线y＝cx2+bx+a的图象大致为（　　）

A． 

B． 

C． 

D．

【分析】根据题意得到a﹣b+c＝0，a＞0，b＜0，c＝﹣1，即可得到抛物线y＝cx2+bx+a的开口向下，对称轴直线x＝﹣＜0，交y轴正半轴，经过点（﹣1，0），据此即可判断．

【解答】解：∵抛物线y＝ax2+bx+c经过（﹣1，0）和（0，﹣1）两点，

∴开口向上，对称轴在y轴的右侧，

∴a﹣b+c＝0，a＞0，b＜0，c＝﹣1，

∴抛物线y＝cx2+bx+a的开口向下，对称轴直线x＝﹣＜0，交y轴正半轴，

当x＝﹣1时，y＝c﹣b+a＝0，

∴抛物线y＝cx2+bx+a经过点（﹣1，0），

故选：B．

10．正方形ABCD中，AB＝4，P为对角线BD上一动点，F为射线AD上一点，若AP＝PF，则△APF的面积最大值为（　　）

A．8 B．6 C．4 D．2

【分析】作PM⊥AD与M，根据正方形的性质易得PM＝DM，设PM＝DM＝x，则AM＝4﹣x，根据等腰三角形的性质即可得出AF＝2（4﹣x），由三角形面积公式得出S△APF＝×2（4﹣x）•x＝﹣x2+4x＝﹣（x﹣2）2+4，根据二次函数的性质即可求得结果．

【解答】解：作PM⊥AD与M，

∵BD是正方形ABCD的对角线，

∴∠ADB＝45°，

∴△BDM是等腰直角三角形，

∴PM＝DM，

设PM＝DM＝x，则AM＝4﹣x，

∵AP＝PF，

∴AM＝FM＝4﹣x，

∴AF＝2（4﹣x），

∵S△APF＝AF•PM，

∴S△APF＝×2（4﹣x）•x＝﹣x2+4x＝﹣（x﹣2）2+4，

∴当x＝2时，S△APF有最大值4，

故选：C．

二、填空题（本大题共4小题，每小题5分，满分20分）

11．（5分）抛物线y＝﹣（x+2）2的顶点坐标是　（﹣2，0）　．

【分析】根据题目中抛物线的解析式，可以直接写出该抛物线的顶点坐标．

【解答】解：∵抛物线y＝﹣（x+2）2，

∴该抛物线的顶点坐标为（﹣2，0），

故答案为：（﹣2，0）．

12．（5分）如图，若芭蕾舞者抬起的脚尖点C分线段AB近似于黄金分割（AC＜BC），已知AB＝160cm，BC的长约为　98.9　cm．（结果精确到0.1cm）

【分析】利用黄金分割的定义得到BC＝AB，再把AB＝160cm代入后进行计算即可．

【解答】解：∵点C为线段AB的黄金分割点（AC＜BC），AB＝160cm，

∴BC＝AB＝×160≈98.9，

故答案为：98.9．

13．（5分）如图，在边长为1的小正方形网格中，点A、B、C均在格点上，则tanB的值为　　．

【分析】如图，取格点E，连接AE，EC，则B，A，E共线，∠E＝90°．利用勾股定理求出EC，EB，可得结论．

【解答】解：如图，取格点E，连接AE，EC，则B，A，E共线，∠E＝90°．

∵EC＝＝，BE＝＝2，

∴tanB＝＝．

故答案为：．

14．（5分）如图，矩形ABCD中，AB＝6，AD＝8，点P是AB边上动点，把△ADP沿DP折叠得△A'DP，射线DA'交射线AB于点Q，

（1）当Q点和B点重合时，PQ长为　　；

（2）当△A'DC为等腰三角形时，则DQ长为　或　．

【分析】（1）根据勾股定理求出BD，即DQ，进而求出A′B，即A′Q，在直角三角形PQA′中，设未知数，列方程求解即可；

（2）分三种情况进行解答，即A′D＝A′C，A′C＝CD，A′D＝CD，分别画出相应的图形，利用等腰三角形的性质，相似三角形的判定和性质以及勾股定理求解即可．

【解答】解：（1）如图1：当Q点与B点重合时，

QD＝DB＝＝＝10，

由翻折变换可得，AD＝A′D＝8，AP＝A′P，

∴BA′＝10﹣8＝2，

设PQ＝x，则AP＝A′P＝6﹣x，

在Rt△PBA′中，由勾股定理得，

A′P2+A′B2＝PB2，

即（6﹣x）2+22＝x2，

解得x＝，

即，

故答案为：；

（2）①当A'D＝A'C＝8时，如图2，

过点A′作A′M⊥CD于M，则DM＝MC＝CD＝3，

在Rt△A′DM中，

A′M＝＝＝，

∵∠DAQ＝∠A′MD＝90°，∠AQD＝∠MDA′，

∴△AQD∽△MDA'，

∴＝，

即＝，

解得DQ＝；

②当A'C＝DC＝6时，如图3，

过点C作CN⊥DQ于N，则DN＝A′N＝A′D＝4，

在Rt△CDN中，由勾股定理得，

CN＝＝＝2，

∵∠DAQ＝∠CND＝90°，∠AQD＝∠NDC，

∴△AQD∽△NDC，

∴＝，

即＝，

解得DQ＝，

③A'D＝AD＝8，CD＝6，所以A'D≠CD，

综上所述，DQ的长为或．

三、（本大题共2小题，每小题8分，满分16分）

15．（8分）计算：2sin245°﹣6cos30°+3tan45°+4sin60°．

【分析】根据特殊锐角的三角函数值代入计算即可．

【解答】解：原式＝2×（）2﹣6×+3×1+4×

＝2×﹣3+3+2

＝1﹣3+3+2

＝4﹣．

16．（8分）如图，二次函数y＝﹣+bx+c的图象经过A（2，0）、B（0，﹣4）两点．

（1）求这个二次函数的解析式；

（2）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．

【分析】（1）二次函数图象经过A（2，0）、B（0，﹣4）两点，两点代入y＝﹣+bx+c，算出b和c，即可得解析式．

（2）先求出对称轴方程，写出C点的坐标，计算出AC，然后由面积公式计算值．

【解答】解：（1）把A（2，0）、B（0，﹣4）代入y＝﹣+bx+c，得：，

解得，

∴这个二次函数的解析式为y＝﹣+3x﹣4．

（2）∵该抛物线对称轴为直线x＝﹣＝3，

∴点C的坐标为（3，0），

∴AC＝OC﹣OA＝3﹣2＝1，

∴S△ABC＝×AC×OB＝×1×4＝2．

四、（本大题共2小题，每小题8分，满分16分）

17．（8分）如图，一次函数y1＝kx+b的图象与反比例函数y2＝的图象交于A、B两点．

（1）利用图中的条件，求反比例函数和一次函数的解析式；

（2）根据图象直接写出使y1＜y2的自变量x取值范围．

【分析】（1）通过读图，可得A、B点的坐标，进而可用待定系数法确定两个函数的解析式．

（2）结合两个函数的图象和A、B点的坐标，找出当一次函数图象在反比例函数图象下方时，自变量x的取值范围即可．

【解答】解：（1）由图象知反比例函数y2＝的图象经过点A（2，1），

∴1＝，

∴m＝2，

∴反比例函数解析式为；y2＝；

∵反比例函数y2＝的图象经过点B（﹣1，n），

∴n＝﹣2，

∴B（﹣1，﹣2），

由图象知一次函数y1＝kx+b的图象经过点A（2，1），B（﹣1，﹣2），

∴，解得，

∴一次函数解析式为y1＝x﹣1．

（2）由图象可得使y1＜y2的自变量x取值范围是x＜﹣1或0＜x＜2．

18．（8分）如图，在网格图中（小正方形的边长为1），△ABC的三个顶点都在格点上．

（1）把△ABC沿着x轴向右平移6个单位得到△A1B1C1，请画出△A1B1C1；

（2）请以坐标系的原点O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2，使得△ABC与△A2B2C2的位似比为1：2；

（3）请直接写出△A2B2C2三个顶点的坐标．

【分析】（1）利用点平移的坐标变换规律写出A1、B1、C1的坐标，然后描点即可；

（2）（3）根据关于原点为位似中心的点的坐标特征，把A、B、C的横纵坐标都乘以﹣2得到A2、B2、C2的坐标，然后描点即可．

【解答】解：（1）如图，△A1B1C1为所作；

（2）如图，△A2B2C2为所作；

（3）△A2B2C2三个顶点的坐标分别为A2（6，0），B2（6，4），C2（2，6）．

五、（本大题共2小题，每小题10分，满分20分）

19．（10分）2020年6月23日，我国第55颗北斗卫星，即北斗全球卫星导航系统最后一颗组网卫星发射成功．北斗导航装备的不断更新，极大方便人们的出行．某中学从A地出发，组织学生利用导航到C地区进行研学活动，已知C地位于A地的正北方向，且距离A地24千米．由于A、C两地间是一块湿地，所以导航显示的路线是沿北偏东60°方向走到B地，再沿北偏西37°方向走一段距离才能到达C地，求A、B两地的距离（精确到1千米）．

（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.7，≈1.4，≈1.7）

【分析】如图，过点B作BD⊥AC于点D，设AD＝x，解直角三角形即可得到结论．

【解答】解：如图，过点B作BD⊥AC于点D，设AD＝x，

则，

∴tan∠BCD＝tan37°＝≈0.7，

解得x＝7，

∴AB＝2x＝14（千米），

答：A、B两地的距离为14千米．

20．（10分）已知：如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，E为直角边AC的中点，过D，E作直线交AB的延长线于F．

（1）若AB＝6，AC＝8，求BD长；

（2）求证：AB•AF＝AC•DF．

【分析】（1）由勾股定理得BC＝10，再证明△ABD∽△CBA，由此可得BD＝3.6；

（2）因为DE是AC边上的中线，所以DE＝CE＝AE，所以△FDB∽△FAD，所以有，又因为，所以即AB•AF＝AC•DF．

【解答】解：（1）∵∠BAC＝90°，AB＝6，AC＝8，

∴BC＝＝10，

∵∠BAC＝90°，AD⊥BC，

∴∠CAB＝∠ADB，

∵∠B＝∠B，

∴△CBA∽△ABD，

∴，

∴，

∴BD＝3.6；

（2）证明：由（1）知：BD：AD＝AB：AC①，

又∵E为AC的中点，AD⊥BC，

∴ED＝AE＝EC，

∴∠C＝∠EDC＝∠FAD＝∠BDF，

又∵∠F为公共角，

∴△DBF∽△ADF，

∴BD：AD＝DF：AF②，

由①②得，AB：AC＝DF：AF，

∴AB•AF＝AC•DF．

六、（本题满分12分）

21．（12分）如图，AB是⊙O的直径，点C，M为⊙O上两点，且C点为的中点，过C点的切线交射线BM、BA于点E、F．

（1）求证：BE⊥FE；

（2）若∠F＝30°，MB＝2，求的长度．

【分析】（1）连接OC，由切线的性质得出∠OCF＝90°，由圆周角定理得出∠EBC＝∠OBC，由平行线的性质可得出结论；

（2）连接OM，证明△OBM为等边三角形，则得出BM＝OB＝2，由弧长公式可得出答案．

【解答】（1）证明：连接OC，

∵FC是⊙O的切线，

∴∠OCF＝90°，

∵点M是的中点，

∴∠EBC＝∠OBC，

∵OB＝OC

∴∠OBC＝∠OCB，

∴∠EBC＝∠OCB，

∴OC∥BE，

∴BE⊥FE；

（2）解：连接OM，

∵∠F＝30°，∠E＝90°，

∴∠FBE＝60°，

又∵OM＝OB，

∴△OBM为等边三角形，

∴BM＝OB＝2，

∴的长为．

七、（本题满分12分）

22．（12分）如图，已知抛物线y1＝a（x﹣1）（x﹣5）和直线y2＝﹣ax﹣a（其中a＞0）相交于A，B两点，抛物线y1与x轴交于C，D两点，与y轴交于点G，直线y2与坐标轴交于E，F两点．

（1）若G的坐标为（0，5），求抛物线y1解析式和直线y2解析式；

（2）求证：直线y2＝﹣ax﹣a始终经过该抛物线y1的顶点；

（3）求的值．

【分析】（1）把G（0，5）代入抛物线解得a＝1，即可得抛物线y1解析式和直线y2解析式；

（2）求出抛物线顶点，代入直线验证即可；

（3）先求出E（﹣1，0），M（2，0），N（3，0），再由OF∥AM∥BN得EF：FA：AB＝EO：OM：MN＝1：2：1，即可求出的值．

【解答】（1）解：把G（0，5）代入抛物线解得a＝1，

∴抛物线解析式为y1＝（x﹣1）（x﹣5）＝x2﹣6x+5，直线解析式为y2＝﹣x﹣1；

（2）证明：∵y1＝a（x﹣1）（x﹣5）与x轴交点为（1，0）和（5，0），

∴其对称轴为直线x＝3，顶点坐标为（3，﹣4a），

∵x＝3时，y2＝﹣3a﹣a＝﹣4a，

∴直线y2＝﹣ax﹣a始终经过该抛物线的顶点；

（3）解：过A，B两点作x轴的垂线，垂足分别为M，N两点，

令y2＝﹣ax﹣a中y＝0，解得x＝﹣1，即E（﹣1，0），

再联立两个解析式a（x﹣1）（x﹣5）＝﹣ax﹣a解得x1＝2，x2＝3，

∴M（2，0），N（3，0），

∵OF∥AM∥BN，

∴EF：FA：AB＝EO：OM：MN＝1：2：1，

∴．

八、（本题满分14分）

23．（14分）如图1，△ABC中，∠ACB＝90°，AC＝BC，E为△ABC的中线BD上的一点，将线段AE以E点为中心逆时针旋转90°得到线段EF，恰EF经过点C．

（1）若∠CAF＝α，则∠CBE＝　2α　（用α的代数式表示）．

（2）如图2，过点C作CH∥AE，交AF于点H，连接BH交EF于点G，

①求证：AF＝BH；

②若CF＝2，求EG的长．

【分析】（1）由直角三角形的性质得出AD＝DE＝DC，由等腰三角形的性质得出∠EAF＝45°，由直角三角形的性质可得出答案；

（2）①证明△ACF≌△BCH（SAS），由全等三角形的性质得出AF＝BH；

②证明△BEG∽△ACF，由相似三角形的性质得出答案．

【解答】解：（1）∵D为AC的中点，∠AEC＝90°，

∴AD＝DE＝DC，

∴∠DAE＝∠AED，

∵AE＝EF，

∴∠EAF＝45°，

∴∠EAD＝45°﹣α，

∴∠DEA＝∠EAD＝45°﹣α，

∴∠BCA＝90°，

∵∠EDC＝90°﹣2α，

∴∠CBE＝2α；

故答案为：2α；

（2）①∵CH∥AE，

∴∠FCH＝∠FEA＝∠BCA＝90°，

∴∠CHF＝∠EAF＝45°，

∴CH＝CF，

在△ACF和△BCH中，∠ACF＝∠BCH，BC＝AC，CH＝CF，

∴△ACF≌△BCH（SAS），

∴AF＝BH；

②由△ACF≌△BCH得∠CAF＝∠CBH，

又由（1）可知∠CBE＝2∠CAF，

∴∠CAF＝∠EBG，

∵DE＝DC，

∴∠DEC＝∠DCE，

即∠BEG＝∠ACF，

∴△BEG∽△ACF，

由BC＝2DC＝2DE，可设BC＝2x，

则CD＝DE＝x，，

∴，

∴，

∵CF＝2，

∴．