2020-2021学年重庆市高二（上）半期考试数学试卷人教A版

这是一份2020-2021学年重庆市高二（上）半期考试数学试卷人教A版，共11页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。


1. 在空间直角坐标系中， A1,4,3，B3,5,2两点的距离为( )
A.6B.7C.22D.3

2. 已知直线l：2x+3y+6=0，则下列说法正确的是（ ）
A.l在x轴上的截距为3B.l在y轴上的截距为2
C.l的倾斜角为锐角D.l的倾斜角为钝角

3. 圆C1：x2+y2=9与圆C2：x2+y2−2x+6y+9=0的公切线的条数为( )
A.4B.3C.2D.1

4. 我国古代著名书籍《九章算术》中写道的“鳖臑”是一种特定的四面体，如图，以四面体ABCD为例，若BC⊥CD，AB⊥平面BCD，则称该四面体为“鳖臑”，则“鳖臑”的表面三角形为直角三角形的个数是（ ）

A.1B.2 C.3D.4

5. 一个几何体的三视图如图所示，则该几何体的体积为（ ）

A.223B.233C.8D.253

6. 若实数x，y满足x+22+y2=1，则y−1x−1的最大值为( )
A.56B.45C.34D.23

7. 已知底面边长为3的正三棱柱的所有顶点均在表面积为16π的球面上，则该三棱柱的侧面积为（ ）
A.18B.93C.123D.183

8. 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也，又以高乘之，三十六成一，该术相当于给出了由圆锥的底面周长L与高ℎ，计算其体积V的近似公式V≈136L2ℎ，它实际上是将圆锥体积公式中的圆周率π近似取为3，那么，近似公式V≈275L2ℎ相当于将圆锥体积公式中的π近似取为（ ）
A.227B.258C.15750D.355113
二、多选题

已知方程x2+y2−2ax+4y+2a2=0a∈R表示圆，则下列说法正确的有（ ）
A.a的取值范围是−2,2B.a的取值范围是−1,3
C.点2,1在圆内D.点2,1在圆外

已知不重合平面α，β和不同直线m，n，则下列条件能推出α//β的是（ ）
A.m⊂α，n⊂β，m//n
B.m⊂α，n⊂α，m∩n=P，m//β，n//β
C.m⊥n，n⊥β，m//α
D.m⊥α，n⊥β，m//n

下列关于正方体ABCD−A1B1C1D1的说法正确的有（ ）
A.BC1与CD1所成角为60∘
B.AB1与平面ABC1D1所成角为30∘
C.二面角A−BD−A1的大小为45∘
D.AC1与平面A1BD所成角为90∘

已知点P在直线x−2y−4=0上运动，过P作圆C:x2+y2=2的两条切线，切点分别记为A，B，C为圆心，则下列说法正确的有（ ）
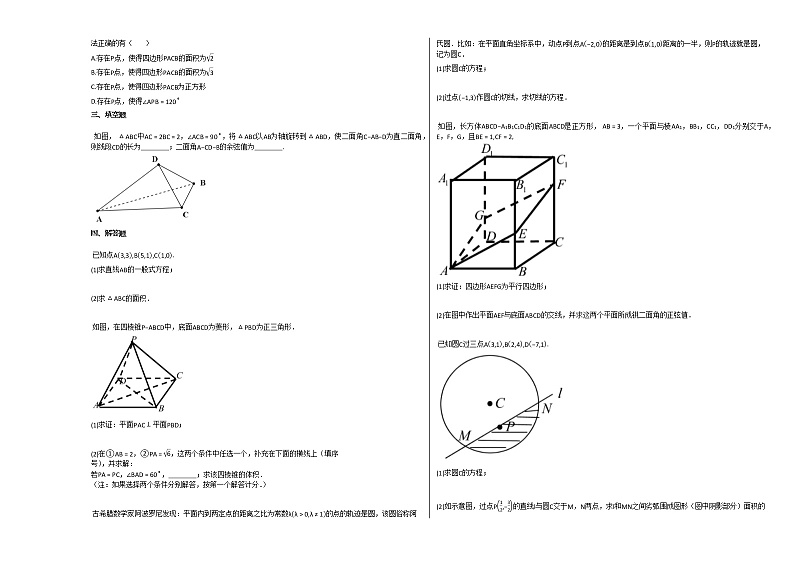
A.存在P点，使得四边形PACB的面积为2
B.存在P点，使得四边形PACB的面积为3
C.存在P点，使得四边形PACB为正方形
D.存在P点，使得∠APB=120∘
三、填空题

如图， △ABC中AC=2BC=2，∠ACB=90∘，将△ABC以AB为轴旋转到△ABD，使二面角C−AB−D为直二面角，则线段CD的长为________；二面角A−CD−B的余弦值为________.

四、解答题

已知点A3,3,B5,1,C1,0.
(1)求直线AB的一般式方程；

(2)求△ABC的面积．

如图，在四棱锥P−ABCD中，底面ABCD为菱形，△PBD为正三角形．

(1)求证：平面PAC⊥平面PBD；

(2)在①AB=2，②PA=6，这两个条件中任选一个，补充在下面的横线上（填序
号），并求解：
若PA=PC，∠BAD=60∘，________；求该四棱锥的体积．
（注：如果选择两个条件分别解答，按第一个解答计分．）

古希腊数学家阿波罗尼发现：平面内到两定点的距离之比为常数λλ>0,λ≠1的点的轨迹是圆，该圆俗称阿氏圆．比如：在平面直角坐标系中，动点P到点A−2,0的距离是到点B1,0距离的一半，则P的轨迹就是圆，记为圆C．
(1)求圆C的方程；

(2)过点−1,3作圆C的切线，求切线的方程．

如图，长方体ABCD−A1B1C1D1的底面ABCD是正方形， AB=3，一个平面与棱AA1，BB1，CC1，DD1分别交于A，E，F，G，且BE=1,CF=2,

(1)求证：四边形AEFG为平行四边形；

(2)在图中作出平面AEF与底面ABCD的交线，并求这两个平面所成锐二面角的正弦值．

已知圆C过三点A3,1,B2,4,D−7,1.

(1)求圆C的方程；

(2)如示意图，过点P12,−32的直线l与圆C交于M，N两点，求l和MN之间劣弧围成图形（图中阴影部分）面积的最小值．

如图，在四面体ABCD中，AB，AC，AD两两垂直， AB=3，AC=2，AD=1.

(1)求△BCD的面积；

(2)设动点P在直线CD上运动，当BP与平面ABC所成角最大时，求AP与平面ABD所成角的正切值.
参考答案与试题解析
2020-2021学年重庆市高二(上)半期考试数学试卷
一、选择题
1.
【答案】
A
【考点】
空间两点间的距离公式
【解析】
直接利用两点之间距离求解即可.
【解答】
解：在空间直角坐标系中， A1,4,3，B3,5,2两点的距离为：
|AB|=(1−3)2+(4−5)2+(3−2)2=6.
故选A.
2.
【答案】
D
【考点】
直线的倾斜角
直线的一般式方程
【解析】
求出直线在x，y轴上的截距以及直线的斜率，进行分析即可得到答案.
【解答】
解：直线l：2x+3y+6=0，
令y=0，可得x=−3，
∴ l在x轴上的截距为−3， 故A错误；
令x=0，可得y=−2，
∴ l在y轴上的截距为−2，故B错误；
∵ 直线l的斜率k=−23<0，
∴ l的倾斜角为钝角，故 C错误，D正确.
故选D.
3.
【答案】
C
【考点】
圆与圆的位置关系及其判定
两圆的公切线条数及方程的确定
【解析】
根据题意，分析两圆的圆心与半径，即可得两圆的位置关系，据此分析可得答案．
【解答】
解：根据题意，圆C1：x2+y2=9，其圆心为0,0，半径R=3；
圆C2：x2+y2−2x+6y+9=0化为标准方程为，
x−12+y+32=1，其圆心为1,−3，半径r=1，
∵ 两圆的圆心距为d=12+(−3)2=10，
∴ R−r∴ 两圆相交，其公切线的有2条.
故选C.
4.
【答案】
D
【考点】
棱锥的结构特征
【解析】
本题考查立体几何里的垂直关系
【解答】
解：△ABC，△ABD，△BCD，△ACD都是直角三角形，合计4个.
故选D.
5.
【答案】
B
【考点】
由三视图求体积
【解析】
本题考查三视图
思路还原立体图，再求立体图形的体积
【解答】
解：依题意，题中的几何体是从一个棱长为2的正方体
ABCD−A1B1C1D1中截去三棱锥B−B1EF （其中点E，F分别是棱B1C1,A1B1的中点）后所剩余的
部分，
因此其体积等于
23−13×12×12×2=233.
故选B．
6.
【答案】
C
【考点】
点到直线的距离公式
圆的标准方程
直线的斜率
直线与圆的位置关系
【解析】
由先判断出方程表示的图形，再给y−1x−1赋与几何意义，判断出当直线与圆相切时斜率最大求出最大值．
【解答】
解：方程x+22+y2=1表示以(−2,0)为圆心，1为半径的圆，
y−1x−1的的几何意义是圆上一点与(1,1)连线的斜率，
设y−1x−1=k，即y=kx−1+1，
当直线y=kx−1+1与圆相切时，斜率k取最大值或最小值.
由|−2k−k+1|k2+12=1可得k=0或k=34，
∴ y−1x−1的最大值为34.
故选C.
7.
【答案】
A
【考点】
球内接多面体
棱柱、棱锥、棱台的侧面积和表面积
【解析】
首先求出球的半径，再求出底面圆半径，从而得到正三棱柱的高，从而得到答案.
【解答】
解：设球的半径为R，则由已知可得4πR2=16π，解得R=2，
底面外接圆半径为r=12×3sin60∘=1，
所以正三棱柱的高ℎ=2R2−r2=24−1=23，
所以正三棱柱的侧面积S=3×3×23=18.
故选A.
8.
【答案】
B
【考点】
柱体、锥体、台体的体积计算
【解析】
根据近似公式V≈275L2ℎ，建立方程，即可求得结论．
【解答】
解：设圆锥底面圆的半径为r，高为ℎ，则L=2πr，
∴ 13πr2ℎ=275(2πr)2ℎ，
∴ π=258．
故选B．
二、多选题
【答案】
A,D
【考点】
点与圆的位置关系
圆的一般方程
圆的标准方程与一般方程的转化
【解析】
本题考查圆的标准方程
【解答】
解：已知方程x2+y2−2ax+4y+2a2=0a∈R表示圆，
整理得(x−a)2+(y+2)2=4−a2a∈R，
故圆的圆心为(a，−2)，且4−a2>0，
∴ −2点2,1与圆心的距离为(2−a)2+(1+2)2，圆的半径为4−a2，
∵ (2−a)2+9−4+a2=2(a−1)2+7>0，
即(2−a)2+9>4−a2，
即(2−a)2+(1+2)2>4−a2，
因此点到圆心的距离大于半径，点2,1在圆外，故C错误，D正确.
故选AD.
【答案】
B,D
【考点】
平面与平面平行的判定
空间中平面与平面之间的位置关系
空间中直线与直线之间的位置关系
【解析】
直接由空间线面关系，逐个推导即可.
【解答】
解：A，此时两平面可能会相交，故不能判断平行，故A错误；
B，为两平面平行的判定定理，故B正确；
C，若m⊥n，n⊥β，则m//β或m⊂β，
此时若m//α，则α//β或α与β相交，故C错误；
D，若n⊥β，m//n则m⊥β，
此时若m⊥α，则α//β，故D正确.
故选BD.
【答案】
A,B,D
【考点】
异面直线及其所成的角
直线与平面所成的角
二面角的平面角及求法
【解析】
直接利用正方体的几何特征判断即可.
【解答】
解：根据题意画出图形，如图：
A，易得△ACD1为等边三角形，故∠AD1C=60∘，又BC1//AD1，
所以直线BC1与CD1所成角为60∘，故A正确；
B，易得B1C⊥平面ABC1D1，
连结AO，则∠B1AO即为直线AB1与平面ABC1D1所成的角，
由于sin∠B1AO=B1OAB1=12，则∠B1AO=30∘，故B正确；
C，连接A1M，由于AA1⊥平面ABCD，在等边三角形A1BD中，A1M⊥BD，则二面角A−BD−A1的平面角即为∠A1MA，
tan∠A1MA=AA1AM=2≠1，则θ≠45∘，故C错误；
D，由于A1D⊥平面ABC1D1，从而A1D⊥AC1，同理可得BD⊥AC1，
A1D∩BD=D，
所以AC1⊥平面A1BD，故AC1与平面A1BD所成角为90∘，故D正确.
故选ABD.
【答案】
B,C
【考点】
直线与圆的位置关系
点到直线的距离公式
圆的综合应用
【解析】
以圆心到直线的距离为轴，逐个判断即可.
【解答】
解：由于四边形PACB面积S=2S△PAC，所以只需考虑△PAC的面积即可，
由于点P到圆心的距离的最小值即为圆心到直线的距离d=−41+4=455>2，
所以PAmin=d2−22=165−2=65，
所以Smin=2×12×2×65=2155>2，故A错误；
又Smin=2155<3，故B正确；
若四边形PACB为正方形，则圆心到点P的距离等于2×2=2，
由于d=455<2，故必然存在点P，满足PC=2，故C正确；
若∠APB=120∘，则∠ACP=30∘，
此时圆心到点P的距离等于2×23=263故不存在P点，满足∠APB=120∘，故D错误.
故选BC.
三、填空题
【答案】
2105,−69
【考点】
二面角的平面角及求法
棱锥的结构特征
点、线、面间的距离计算
【解析】
首先找到二面角的平面角，再解三角形即可.
【解答】
解：如图，作CM⊥AB于点M，连结DM，则DM⊥CM，DM=CM，
∴ ∠DMC为二面角C−AB−D的平面角，即∠DMC=90∘，
由于AC=2BC=2，∠ACB=90∘，则AB=5，
∴ DM=CM=1×25=255，则CD=2×255=2105，
取CD的中点N，由于AD=AC，BC=BD，
∴ AN⊥CD，BN⊥CD，
∴ ∠ANB为二面角A−CD−B的平面角，
过B作BE⊥AN，交AN的延长线于点E，
∵ AB⊥平面DCM，
∴ AB⊥CD，又BN⊥CD，
∴ CD⊥平面ABN,
∴ CD⊥BE，
∴ BE⊥平面ACD.
∵ VD−ABC=VB−ADC，，
又AN=4−1052=3105，BN=1−1052=155，
∴ 13×12×2×1×255=13×12×2105×3105⋅BE，
解得，BE=256，
∴ sin∠BNE=BEBN=539，
显然∠ANB是钝角,
∴ cs∠ANB=−1−(539)2=−69.
故答案为：2105；−69.
四、解答题
【答案】
解：(1)∵ A3,3，B5,1，
∴ 直线AB的方程为y−31−3=x−35−3⇒x+y−6=0．
(2) |AB|=3−52+3−12=22；
点C1,0到直线AB的距离d=|1+0−6|12+12=522，
∴ △ABC的面积S=12|AB|⋅d=5．
【考点】
直线的两点式方程
两点间的距离公式
点到直线的距离公式
【解析】
无
无
【解答】
解：(1)∵ A3,3，B5,1，
∴ 直线AB的方程为y−31−3=x−35−3⇒x+y−6=0．
(2) |AB|=3−52+3−12=22；
点C1,0到直线AB的距离d=|1+0−6|12+12=522，
∴ △ABC的面积S=12|AB|⋅d=5．
【答案】
(1)证明：设AC∩BD=O，
∵ 底面ABCD为菱形，
∴ AC⊥BD，且O为BD中点；
∵ △PBD为正三角形，
∴ PO⊥BD ，
又PO∩AC=O，
∴ BD⊥平面PAC，
又BD⊂平面PBD，
∴ 平面PAC⊥平面PBD．
(2)解：若选①，则
∵ 底面ABCD为菱形， ∠BAD=60∘，AB=2，
∴ 底面ABCD面积S=23，
∵ PA=PC，O为AC中点，
∴ PO⊥AC，又PO⊥BD ，
∴ PO⊥平面ABCD；
∵ △PBD为正三角形，∴ PO=3BO=3；
∴ 四棱锥P−ABCD的体积为V=13S⋅PO=2．
若选②，则∵ PA=PC，O为AC中点，
∴ PO⊥AC，又PO⊥BD ，
∴ PO⊥平面ABCD；
设AB=a，∠BAD=60∘，△PBD为正三角形，
∴ AO=PO=32a
∵ AO2+OP2=PA2=6，
∴ a=2，
∴ 四棱锥P−ABCD的体积为V=13S⋅PO=2．
【考点】
平面与平面垂直的判定
柱体、锥体、台体的体积计算
【解析】
无
无
【解答】
(1)证明：设AC∩BD=O，
∵ 底面ABCD为菱形，
∴ AC⊥BD，且O为BD中点；
∵ △PBD为正三角形，
∴ PO⊥BD ，
又PO∩AC=O，
∴ BD⊥平面PAC，
又BD⊂平面PBD，
∴ 平面PAC⊥平面PBD．
(2)解：若选①，则
∵ 底面ABCD为菱形， ∠BAD=60∘，AB=2，
∴ 底面ABCD面积S=23，
∵ PA=PC，O为AC中点，
∴ PO⊥AC，又PO⊥BD ，
∴ PO⊥平面ABCD；
∵ △PBD为正三角形，∴ PO=3BO=3；
∴ 四棱锥P−ABCD的体积为V=13S⋅PO=2．
若选②，则∵ PA=PC，O为AC中点，
∴ PO⊥AC，又PO⊥BD ，
∴ PO⊥平面ABCD；
设AB=a，∠BAD=60∘，△PBD为正三角形，
∴ AO=PO=32a
∵ AO2+OP2=PA2=6，
∴ a=2，
∴ 四棱锥P−ABCD的体积为V=13S⋅PO=2．
【答案】
解：(1)设Px,y，A−2,0，B1,0 ，
∵ |PA|=12|PB|，
∴ x+22+y2=12x−12+y2，
化简，圆C的方程为： x2+y2+6x+5=0．
(2)x2+y2+6x+5=0⇒x+32+y2=4
当切线l的斜率存在时，设l:y−3=kx+1⇒kx−y+k+3=0，
则圆心−3,0到l的距离d=|3−2k|k2+1，r=2，
∴ |3−2k|k2+1=2，解得： k=512，
l:5x−12y+41=0，
当切线l的斜率不存在时， l:x=−1，
圆心−3,0到l的距离d=2=r，成立．
综上：切线方程为： x=−1，或5x−12y+41=0．
【考点】
轨迹方程
点到直线的距离公式
直线与圆的位置关系
圆的切线方程
【解析】
无
无
【解答】
解：（1）设Px,y，A−2,0，B1,0 ，
∵ |PA|=12|PB|，
∴ x+22+y2=12x−12+y2，
化简，圆C的方程为： x2+y2+6x+5=0．
(2)x2+y2+6x+5=0⇒x+32+y2=4
当切线l的斜率存在时，设l:y−3=kx+1⇒kx−y+k+3=0，
则圆心−3,0到l的距离d=|3−2k|k2+1，r=2，
∴ |3−2k|k2+1=2，解得： k=512，
l:5x−12y+41=0，
当切线l的斜率不存在时， l:x=−1，
圆心−3,0到l的距离d=2=r，成立．
综上：切线方程为： x=−1，或5x−12y+41=0．
【答案】
(1)证明：由长方体ABCD−A1B1C1D1可知，平面ABB1A1//平面DCC1D1，
又平面AEFG∩平面ABB1A1=AE，平面AEFG∩平面DCC1D1=GF，
∴ AE//GF ，
同理可证： EF//AG ，
∴ 四边形AEFG为平行四边形．
(2)解：作图如下，设FE∩CB=H，则AH即为平面AEF与底面ABCD的交线．
作BO⊥AH于O，连接OE，
∵ EB⊥平面ABH，
∴ EB⊥AH，∴ AH⊥平面BOE，
∴ OE⊥AH，
∴ ∠BOE为平面AEF与底面ABCD所成二面角的平面角．
∵ CF=2，BE=1，
∴ BH=BC=3，
∴ OB=322,
∴ OE=OB2+EB2=222，
∴ sin∠BOE=EBOE=2211．
【考点】
棱柱的结构特征
两条直线平行的判定
二面角的平面角及求法
【解析】
无
无
【解答】
(1)证明：由长方体ABCD−A1B1C1D1可知，平面ABB1A1//平面DCC1D1，
又平面AEFG∩平面ABB1A1=AE，平面AEFG∩平面DCC1D1=GF，
∴ AE//GF ，
同理可证： EF//AG ，
∴ 四边形AEFG为平行四边形．
(2)解：作图如下，设FE∩CB=H，则AH即为平面AEF与底面ABCD的交线．
作BO⊥AH于O，连接OE，
∵ EB⊥平面ABH，
∴ EB⊥AH，∴ AH⊥平面BOE，
∴ OE⊥AH，
∴ ∠BOE为平面AEF与底面ABCD所成二面角的平面角．
∵ CF=2，BE=1，
∴ BH=BC=3，
∴ OB=322,
∴ OE=OB2+EB2=222，
∴ sin∠BOE=EBOE=2211．
【答案】
解：(1)设圆C的方程x2+y2+Dx+Ey+F=0，
将A3,1，B2,4，D−7,1代入得,
10+3D+E+F=0，20+2D+4E+F=0，50−7D+E+F=0，
解得D=4，E=−2，F=−20，
∴ 圆C：x2+y2+4x−2y−20=0．
(2)连接CM，CN，为使图形面积最小，只需线段MN最短，
由(1)知圆的标准方程为(x+2)2+(y−1)2=25，
即圆心C(−2,1)，半径r=5，
设点C到l的距离为d，则|MN|=2r2−d2=225−d2，
又d≤|CP|=(12+2)2+(−32−1)2=522，
当且仅当l⊥CP时取等，且|MN|min=52，
由勾股定理易知此时∠MCN=90∘，
∴ 所求图形面积的最小值为π×r24−12r2=25π−504．
【考点】
圆的一般方程
点到直线的距离公式
圆的综合应用
【解析】
无
无
【解答】
解：(1)设圆C的方程x2+y2+Dx+Ey+F=0，
将A3,1，B2,4，D−7,1代入得,
10+3D+E+F=0，20+2D+4E+F=0，50−7D+E+F=0，
解得D=4，E=−2，F=−20，
∴ 圆C：x2+y2+4x−2y−20=0．
(2)连接CM，CN，为使图形面积最小，只需线段MN最短，
由(1)知圆的标准方程为(x+2)2+(y−1)2=25，
即圆心C(−2,1)，半径r=5，
设点C到l的距离为d，则|MN|=2r2−d2=225−d2，
又d≤|CP|=(12+2)2+(−32−1)2=522，
当且仅当l⊥CP时取等，且|MN|min=52，
由勾股定理易知此时∠MCN=90∘，
∴ 所求图形面积的最小值为π×r24−12r2=25π−504
【答案】
解：(1)作AE⊥BC于E，连接DE，
∴ AD⊥AB，AD⊥AC，
∴ AD⊥平面ABC，
∴ AD⊥BC，
∴ BC⊥平面ADE，
∴ BC⊥DE．
△ABC中，BC=AB2+AC2=13，AE=AB⋅ACBC=613，
∴ DE=AD2+AE2=713，
∴ △BCD的面积S=12BC⋅DE=72．
(2)作PF⊥AC于F，易得PF⊥平面ABC，
连接BF，则∠PBF为BP与平面ABC所成角，记为θ．
设PF=x，
易知△PFC∼△DAC，∴ FC=2PF=2x，
当P在线段DC的延长线时，
BF=AB2+AF2=9+(2+2x)2，
∴ tanθ=FPBF=x9+2+2x2；
当P在线段CD上及其延长线上时，
BF=AB2+AF2=9+(2x−2)2，
tanθ=x9+2x−22，
显然对相同的x（x>0），
x9+2+2x2∴ tanθ=x9+2x−22=113x2−8x+4
=1131x−4132+3613，
当1x=413⇒x=134时，tanθ取得最大值，也即θ最大．
此时P在线段CD的延长线上，如图，作PG⊥AD于G，因AB⊥平面ACD
∴ PG⊥AB，
∴ PG⊥平面ABD，
∴ ∠PAG为AP与平面ABD所成角，
AG=PF=x=134，PG=AF=2x−2=92，
∴ tan∠PAG=PGAG=1813,
即AP与平面ABD所成角的正切值1813.
【考点】
直线与平面垂直的判定
直线与平面垂直的性质
二次函数在闭区间上的最值
直线与平面所成的角
【解析】
无
无
【解答】
解：(1)作AE⊥BC于E，连接DE，
∴ AD⊥AB，AD⊥AC，
∴ AD⊥平面ABC，
∴ AD⊥BC，
∴ BC⊥平面ADE，
∴ BC⊥DE．
△ABC中，BC=AB2+AC2=13，AE=AB⋅ACBC=613，
∴ DE=AD2+AE2=713，
∴ △BCD的面积S=12BC⋅DE=72．
(2)作PF⊥AC于F，易得PF⊥平面ABC，
连接BF，则∠PBF为BP与平面ABC所成角，记为θ．
设PF=x，
易知△PFC∼△DAC，∴ FC=2PF=2x，
当P在线段DC的延长线时，
BF=AB2+AF2=9+(2+2x)2，
∴ tanθ=FPBF=x9+2+2x2；
当P在线段CD上及其延长线上时，
BF=AB2+AF2=9+(2x−2)2，
tanθ=x9+2x−22，
显然对相同的x（x>0），
x9+2+2x2∴ tanθ=x9+2x−22=113x2−8x+4
=1131x−4132+3613，
当1x=413⇒x=134时，tanθ取得最大值，也即θ最大．
此时P在线段CD的延长线上，如图，作PG⊥AD于G，因AB⊥平面ACD
∴ PG⊥AB，
∴ PG⊥平面ABD，
∴ ∠PAG为AP与平面ABD所成角，
AG=PF=x=134，PG=AF=2x−2=92，
∴ tan∠PAG=PGAG=1813,
即AP与平面ABD所成角的正切值1813.