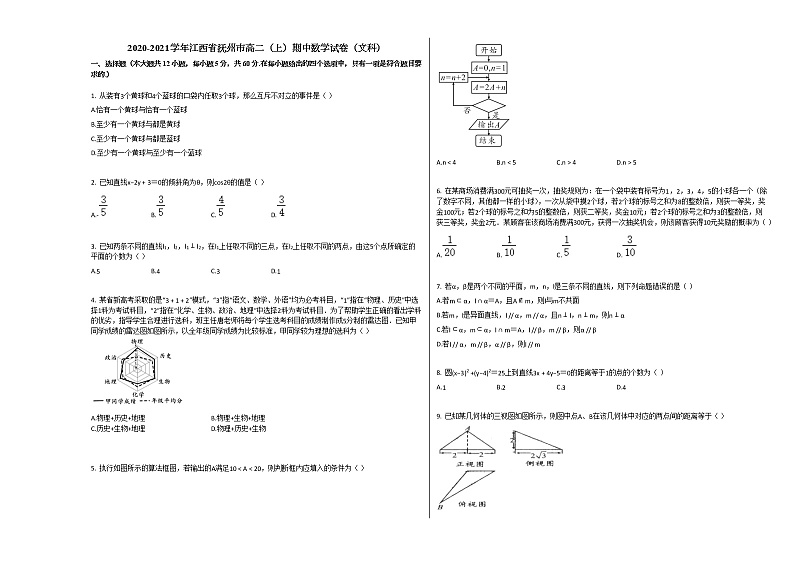
2020-2021学年江西省抚州市高二（上）期中数学试卷（文科）人教A版

这是一份2020-2021学年江西省抚州市高二（上）期中数学试卷（文科）人教A版，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 从装有3个黄球和4个蓝球的口袋内任取3个球，那么互斥不对立的事件是（ ）
A.恰有一个黄球与恰有一个蓝球
B.至少有一个黄球与都是黄球
C.至少有一个黄球与都是蓝球
D.至少有一个黄球与至少有一个蓝球

2. 已知直线x−2y+3＝0的倾斜角为θ，则cs2θ的值是（ ）
A.-B.C.D.

3. 已知两条不同的直线l1，l2，l1⊥l2，在l1上任取不同的三点，在l2上任取不同的两点，由这5个点所确定的平面的个数为（ ）
A.5B.4C.3D.1

4. 某省新高考采取的是“3+1+2”模式，“3”指“语文、数学、外语”均为必考科目，“1”指在“物理、历史”中选择1科为考试科目，“2”指在“化学、生物、政治、地理”中选择2科为考试科目．为了帮助学生正确的看出学科的优劣，指导学生合理进行选科，班主任唐老师将每个学生选考科目的成绩制作成5分制的雷达图．已知甲同学成绩的雷达图如图所示，以全年级同学成绩为比较标准，甲同学较为理想的选科为（ ）

A.物理+历史+地理B.物理+生物+地理
C.历史+生物+地理D.物理+历史+生物

5. 执行如图所示的算法框图，若输出的A满足10
A.n<4B.n<5C.n>4D.n>5

6. 在某商场消费满300元可抽奖一次，抽奖规则为：在一个袋中装有标号为1，2，3，4，5的小球各一个（除了数字不同，其他都一样的小球），一次从袋中摸2个球，若2个球的标号之和为8的整数倍，则获一等奖，奖金100元；若2个球的标号之和为5的整数倍，则获二等奖，奖金10元；若2个球的标号之和为3的整数倍，则获三等奖，奖金2元．某顾客在该商场消费满300元，获得一次抽奖机会，则该顾客获得10元奖励的概率为（ ）
A.B.C.D.

7. 若α，β是两个不同的平面，m，n，l是三条不同的直线，则下列命题错误的是（ ）
A.若m⊂α，l∩α＝A，且A∉m，则l与m不共面
B.若m，l是异面直线，l // α，m // α，且n⊥l，n⊥m，则n⊥α
C.若l⊂α，m⊂α，l∩m＝A，l // β，m // β，则α // β
D.若l // α，m // β，α // β，则l // m

8. 圆(x−3)2+(y−4)2＝25上到直线3x+4y−5＝0的距离等于1的点的个数为（ ）
A.1B.2C.3D.4

9. 已知某几何体的三视图如图所示，则图中点A、B在该几何体中对应的两点间的距离等于（ ）

A.42B.26C.25D.23

10. 某博物馆举办文物知识竞答赛，对该馆内的100名参赛职员所得成绩制成如图所示的频率分布直方图（假定成绩均匀分布），并规定成绩前20名进行奖励，则受奖分数线为（ ）

A.84B.85C.86D.88

11. 在三棱锥P−ABC中，PA⊥平面ABC，PA＝AB＝BC＝AC，M是PC上一点，CM＝2MP，则直线BM与平面ABC所成角的正切值为（ ）
A.B.C.D.3

12. 已知圆C1:x2+y2+2x+4y+4＝0，圆C2:x2+y2−4x+2y+1＝0，M，N分别为圆C1和圆C2上的动点，P为直线l:y＝x+2上的动点，则|MP|+|NP|的最小值为（ ）
A.2−3B.2+3C.−3D.+3
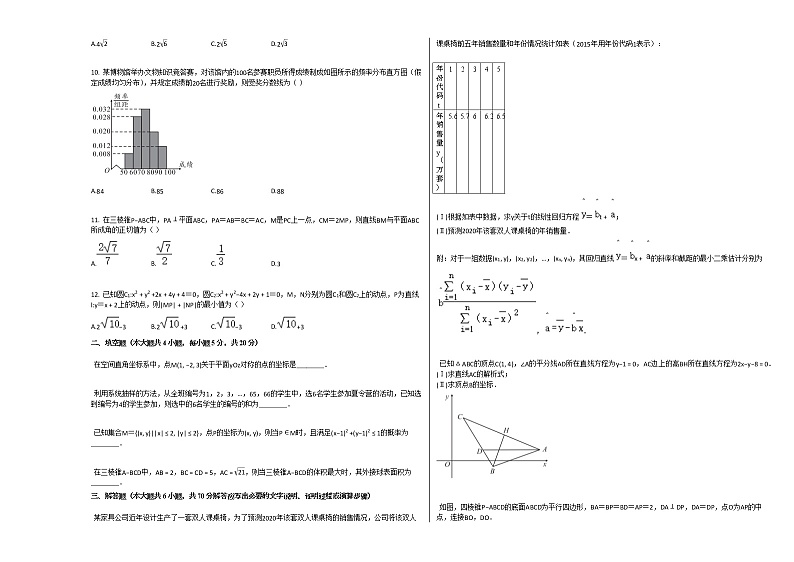
二、填空题（本大题共4小题，每小题5分，共20分）

在空间直角坐标系中，点M(1, −2, 3)关于平面yOz对称的点的坐标是________．

利用系统抽样的方法，从全班编号为1，2，3，…，65，66的学生中，选6名学生参加夏令营的活动，已知选到编号为4的学生参加，则选中的6名学生的编号的和为________．

已知集合M＝{(x, y)||x|≤2, |y|≤2}，点P的坐标为(x, y)，则当P∈M时，且满足(x−1)2+(y−1)2≤1的概率为________．

在三棱锥A−BCD中，AB=2，BC=CD=5，AC=21，则当三棱锥A−BCD的体积最大时，其外接球表面积为________．
三、解答题（本大题共6小题，共70分解答应写出必要的文字说明、证明过程或演算步骤）

某家具公司近年设计生产了一套双人课桌椅，为了预测2020年该套双人课桌椅的销售情况，公司将该双人课桌椅前五年销售数量和年份情况统计如表（2015年用年份代码1表示）：
(Ⅰ)根据如表中数据，求y关于t的线性回归方程＝t+；
(Ⅱ)预测2020年该套双人课桌椅的年销售量．
附：对于一组数据(x1, y)，(x2, y2)，…，(xn, yn)，其回归直线＝x+的斜率和截距的最小二乘估计分别为，．

已知△ABC的顶点C(1, 4)，∠A的平分线AD所在直线方程为y−1=0，AC边上的高BH所在直线方程为2x−y−8=0．
(Ⅰ)求直线AC的解析式；
(Ⅱ)求顶点B的坐标．


如图，四棱锥P−ABCD的底面ABCD为平行四边形，BA＝BP＝BD＝AP＝2，DA⊥DP，DA＝DP，点O为AP的中点，连接BO，DO．
(Ⅰ)求证：AP⊥平面BOD；
(Ⅱ)求点A到平面PBD的距离．


已知高二（1）班60名学生参加体能测试，其测试成绩统计如图所示
(Ⅰ)求该班体能测试成绩在[90, 100]的学生人数；
(Ⅱ)若同一组中的数据用该组区间的中点值作代表，求该班学生参加体能测试的平均成绩；
(Ⅲ)现按照成绩，使用分层抽样的方法在该班成绩位于[80, 90),[90, 100]的学生中随机抽取6人，再从这6人中随机抽取2人，求这两人的成绩一个位于[80, 90)，一个位于[90, 100]的概率．


已知圆C经过O(0, 0)和M(−，）点，且圆心在y轴上．
(Ⅰ)求圆C的标准方程；
(Ⅱ)已知P(x, y)是直线kx+y+4＝0(k>0)上一动点，PA，PB是圆C的两条切线，A，B是切点，若四边形PACB的最小面积是2，求k的值．

如图，在空间几何体ABCDE中，平面ABDE⊥平面ABC，四边形ABDE为正方形，BA⊥AC，BA＝AC，P，Q分别为AE，BC的中点．
(Ⅰ)求证：PQ // 平面CDE；
(Ⅱ)求平面ABDE与平面CDE所成锐二面角的大小．

参考答案与试题解析
2020-2021学年江西省抚州市高二（上）期中数学试卷（文科）
一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）
1.
【答案】
A
【考点】
互斥事件与对立事件
【解析】
利用互斥事件、对立事件的定义直接求解．
【解答】
从装有3个黄球和4个蓝球的口袋内任取3个球，不同的取球情况共有以下4种：
①3个球全是黄球；②2个黄球和1个蓝球；③1个黄球2个蓝球；④3个球全是蓝球．
对于A，恰有一个黄球是情况③，恰有一个蓝球是情况②，
∴ 恰有一个黄球与恰有一个蓝球是互斥不对立的事件，故A正确；
对于B，至少有一个黄球是情况①②③，都是黄球是情况①，
∴ 至少有一个黄球与都是黄球能同时发生，不是互斥事件，故B错误；
对于C，至少有一个黄球是情况①②③，都是蓝球是情况④，
∴ 至少有一个黄球与都是蓝球是对立事件，故C错误；
对于D，至少有一个黄球是情况①②③，至少有一个蓝球是情况②③④，
∴ 至少有一个黄球与至少有一个蓝球能同时发生，不是互斥事件，故D错误．
2.
【答案】
B
【考点】
直线的倾斜角
二倍角的三角函数
【解析】
由题意利用直线的倾斜角和斜率，求得tanθ的值，再利用同角三角函数的基本关系、二倍角公式，求得cs2θ的值．
【解答】
∵ 直线x−2y+3＝0的倾斜角为θ，故tanθ＝，
则cs2θ＝＝＝＝，
3.
【答案】
D
【考点】
平面的基本性质及推论
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
B
【考点】
进行简单的合情推理
【解析】
由雷达图得到甲同学各科与年级平均分相比较的优劣，根据“3+1+2”模式的规则，即可得到甲同学较为理想的选科科目．
【解答】
由雷达图得，甲同学物理，地理科目的分数高于年级平均分，
但物理，历史中只能选择1科为考试科目，
则甲同学较为理想的选科为物理+生物+地理．
5.
【答案】
C
【考点】
程序框图
【解析】
由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量A的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
【解答】
模拟程序的运行，可得
第一次循环，n＝1，A＝2×0+1＝1，不满足10第二次循环，n＝3，A＝2×1+3＝5，不满足10第三次循环，n＝5，A＝2×5+5＝15，满足10所以判断框内应填入的条件为n>4．
6.
【答案】
C
【考点】
古典概型及其概率计算公式
【解析】
从袋中摸2个球的所有标号的情况有10种，利用列举法能求出2个球的标号之和，由此能求出该顾客获得10元奖励的概率．
【解答】
从袋中摸2个球的所有标号的情况为：
(1, 2)，(1, 3)，(1, 4)，(1, 5)，(2, 3)，(2, 4)，(2, 5)，(3, 4)，(3, 5)，(4, 5)，
则2个球的标号之和分别为3，4，5，6，5，6，7，7，8，9，
∴ 2个球的标号之和为5的整数有2种情况，
∴ 该顾客获得10元奖励的概率为P＝．
7.
【答案】
D
【考点】
命题的真假判断与应用
空间中直线与平面之间的位置关系
空间中直线与直线之间的位置关系
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
C
【考点】
直线与圆的位置关系
【解析】
确定圆心和半径，求出圆心到直线的距离，与半径比较，可得选项．
【解答】
(x−3)2+(y−4)2＝25是一个以(3, 4)为圆心，5为半径的圆．
圆心到直线3x+4y−5＝0的距离为d＝＝4，
圆上共有三个点与直线距离为1．
9.
【答案】
C
【考点】
由三视图求体积
【解析】
画出几何体的直观图，利用三视图的数据求解即可．
【解答】
由题意，几何体的直观图如图，是三棱锥，AD垂直底面BCD，CD＝2，
AD＝2，B到CD的距离为23，D为BC在CD上的射影的中点，
所以，BD=22+(23)2=4，AB=42+22=25．
10.
【答案】
C
【考点】
频率分布直方图
【解析】
求出频率分布直方图得竞赛成绩在90∼100分的人数为12，竞赛成绩在80∼90的人数为20，从而受奖分数线在80∼90之间，设受奖分数线为x，利用频率分布直方图列出方程，由此能求出结果．
【解答】
由频率分布直方图得：
竞赛成绩在90∼100分的人数为0.012×10×100＝12，
竞赛成绩在80∼90的人数为0.02×10×100＝20，
故受奖分数线在80∼90之间，
设受奖分数线为x，
则(90−x)×0.02+0.012×10＝0.20，
解得x＝86．
11.
【答案】
A
【考点】
直线与平面所成的角
【解析】
设PA＝3，过点M作MN // PA，交AC于点N，连接BN，推导出∠MBN是直线BM与平面ABC所成角，由此能求出直线BM与平面ABC所成角的正切值．
【解答】
设PA＝3，过点M作MN // PA，交AC于点N，连接BN，
∵ MN // PA，∴ ，
∴ MN＝2，CN＝2，∴ AN＝1，
在△ABN中，BN＝＝＝，
∵ PA⊥平面ABC，MN // PA，∴ MN⊥平面ABC，
∴ ∠MBN是直线BM与平面ABC所成角，
∴ tan∠MBN＝＝＝．
故直线BM与平面ABC所成角的正切值为．
12.
【答案】
A
【考点】
圆与圆的位置关系及其判定
直线和圆的方程的应用
【解析】
根据题意，分析圆C1与圆C2的圆心和半径，求出与圆C1关于直线l对称的圆，再设圆C′上的点M′与圆C1上点M对称，分析可得原问题可以转化为P到圆C′和圆C2上的动点距离之和最小值问题，据此分析可得答案．
【解答】
根据题意，圆C1:x2+y2+2x+4y+4＝0，即(x+1)2+(y+2)2＝1，其圆心为(−1, −2)，半径R＝1，
圆C2:x2+y2−4x+2y+1＝0，即(x−2)2+(y+1)2＝4，其圆心为(2, −1)，半径r＝2，
圆C1关于直线直线l:y＝x+2对称的圆为圆C′，其圆心为(−4, 1)，半径R′＝1，则其方程为(x+4)2+(y−1)2＝1，
设圆C′上的点M′与圆C1上点M对称，则有|PM|＝|PM′|，
原问题可以转化为P到圆C′和圆C2上的动点距离之和最小值问题，
连接C2C′，与直线l交于点P′，点P′是满足|PN|+|PM′|最小的点，此时|PN|+|PM′|＝|C2C′|−3＝2−3，
即|MP|+|NP|的最小值为2−3，
二、填空题（本大题共4小题，每小题5分，共20分）
【答案】
(−1, −2, 3)
【考点】
空间中的点的坐标
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
189
【考点】
系统抽样方法
【解析】
根据系统抽样的定义，求出样本间隔，再根据等差数列的求和公式即可求出．
【解答】
由题意，抽样距为＝11，故选中的6名学生的编号组成一个等差数列，其首项为4，公差为11，
则选中的6名学生的编号的和为4×6+×11＝189，
故答案为：189．
【答案】
【考点】
几何概型计算（与长度、角度、面积、体积有关的几何概型）
【解析】
分别求出正方形和圆的面积，求出满足条件的概率即可．
【解答】
如图示：
集合M所在的区域为正方形ABCD及其内部，
(x−1)2+(y−1)2≤1所在的区域是以(1, 1)为圆心，以1为半径的圆及其内部，
则所求的概率p＝＝，
【答案】
50π
【考点】
球的表面积和体积
球内接多面体
柱体、锥体、台体的体积计算
【解析】
由题意画出图形，可知△ABC为Rt△，要使四面体ABCD的体积最大，则CD⊥平面ABC，取三角形ABC的外心，进一步找出四面体外接球的球心，求出半径，则答案可求．
【解答】
如图，∵ AB=2，BC=CD=5，AC=21，AB2+AC2=BC2，∴ △BCD为等腰三角形，
要使四面体ABCD的体积最大，则CD⊥平面ABC，
三棱锥A−BCD放置在边长为2，5，21的长方体中，DB是扩展后的长方体的对角线，
BD的中点是三棱锥外接球的球心
即O为四面体ABCD的外接球的球心，此时半径OB=BD2=25+252=522．
则外接球的表面积为4π×(522)2=50π．
三、解答题（本大题共6小题，共70分解答应写出必要的文字说明、证明过程或演算步骤）
【答案】
（1），，
＝(−2)×(−0.4)+(−1)×(−0.3)+0+1×0.2+2×0.5＝2.3，
，
则，．
∴ y关于t的线性回归方程为；
（2）当t＝6时，．
即预测2020年该套双人课桌椅的年销售量为6.69万套．
【考点】
求解线性回归方程
【解析】
(Ⅰ)由已知求得与的值，可得y关于t的线性回归方程；
(Ⅱ)在(Ⅰ)中求得的线性回归方程中，取t＝6求得的值即可．
【解答】
（1），，
＝(−2)×(−0.4)+(−1)×(−0.3)+0+1×0.2+2×0.5＝2.3，
，
则，．
∴ y关于t的线性回归方程为；
（2）当t＝6时，．
即预测2020年该套双人课桌椅的年销售量为6.69万套．
【答案】
（1）∵ AC边上的高BH所在直线方程为2x−y−8=0，
∴ AC⊥BH，kBH=2，
∴ kAC⋅kBH=−1．
∴ kAC=−12，
则直线AC的方程为y−4=−12(x−1)，即x+2y−9=0．
（2）联立x+2y−9＝0y−1＝0，解得x＝7y＝1，∴ A(7, 1)，
由题意，kAB=−kAC=12，
则直线AB的方程为y−1=12(x−7)，即x−2y−5=0，
联立2x−y−8＝0x−2y−5＝0，解得x＝113y＝−23，
∴ B(113, −23)．
【考点】
直线的一般式方程与直线的性质
【解析】
(Ⅰ)由AC边上的高BH所在直线方程为2x−y−8=0，可得AC⊥BH，kBH，即可得到kAC，利用点斜式即可得到直线AC的方程；
(Ⅱ)求出直线AB的方程，与BH所在直线方程联立即可求得点B的坐标．
【解答】
（1）∵ AC边上的高BH所在直线方程为2x−y−8=0，
∴ AC⊥BH，kBH=2，
∴ kAC⋅kBH=−1．
∴ kAC=−12，
则直线AC的方程为y−4=−12(x−1)，即x+2y−9=0．
（2）联立x+2y−9＝0y−1＝0，解得x＝7y＝1，∴ A(7, 1)，
由题意，kAB=−kAC=12，
则直线AB的方程为y−1=12(x−7)，即x−2y−5=0，
联立2x−y−8＝0x−2y−5＝0，解得x＝113y＝−23，
∴ B(113, −23)．
【答案】
（1）证明：∵ DA＝DP，点O为AP的中点，
∴ DO⊥AP，同理BO⊥AP，
又DO∩BO＝O，∴ AP⊥平面BOD；
（2）∵ BA＝BP＝AP＝2，∴ △ABP为等边三角形，BO＝，
∵ DA⊥DP，DA＝DP，∴ DO⊥APAP＝8，
∴ OB2+OD2＝BD5，得OB⊥OD，
又DO⊥AP，AP∩OB＝O，
设点A到平面PBD的距离为ℎ，
由VA−PBD＝VD−PAB得，，
即，
解得ℎ＝．
即点A到平面PBD的距离为．
【考点】
直线与平面垂直
点、线、面间的距离计算
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
（1）由题意得该班体能测试成绩在[90, 100]的学生人数为60×0.005×10＝3．
（2）由题意得平均数为：
＝35×0.025+45×0.15+55×0.2+65×0.25+75×0.225+85×0.1+95×0.05＝65．
(Ⅲ)由题意得分数在[80, 90),[90, 100]的学生人数分别为4，2，
记成绩在[80, 90)的学生为A，B，C，D，成绩在[90, 100]的学生为a，b，
则随机抽取2人，可能的情况有15种，分别为：
(A, B)，(A, C)，(A, D)，(A, a)，(A, b)，(B, C)，(B, D)，(B, a)，(B, b)，
(C, D)，(C, a)，(C, b)，(D, a)，(D, b)，(a, b)，
这两人的成绩一个位于[80, 90)，一个位于[90, 100]包含的基本事件有8种，分别为：
(A, a)，(A, b)，(B, a)，(B, b)，(C, a)，(C, b)，(D, a)，(D, b)，
∴ 这两人的成绩一个位于[80, 90)，一个位于[90, 100]的概率p＝．
【考点】
频率分布直方图
【解析】
(Ⅰ)由频率分布直方图能求出该班体能测试成绩在[90, 100]的学生人数．
(Ⅱ)由频率分布直方图能求出平均数．
(Ⅲ)分数在[80, 90),[90, 100]的学生人数分别为4，2，记成绩在[80, 90)的学生为A，B，C，D，成绩在[90, 100]的学生为a，b，随机抽取2人，利用列举法能求出这两人的成绩一个位于[80, 90)，一个位于[90, 100]的概率．
【解答】
（1）由题意得该班体能测试成绩在[90, 100]的学生人数为60×0.005×10＝3．
（2）由题意得平均数为：
＝35×0.025+45×0.15+55×0.2+65×0.25+75×0.225+85×0.1+95×0.05＝65．
(Ⅲ)由题意得分数在[80, 90),[90, 100]的学生人数分别为4，2，
记成绩在[80, 90)的学生为A，B，C，D，成绩在[90, 100]的学生为a，b，
则随机抽取2人，可能的情况有15种，分别为：
(A, B)，(A, C)，(A, D)，(A, a)，(A, b)，(B, C)，(B, D)，(B, a)，(B, b)，
(C, D)，(C, a)，(C, b)，(D, a)，(D, b)，(a, b)，
这两人的成绩一个位于[80, 90)，一个位于[90, 100]包含的基本事件有8种，分别为：
(A, a)，(A, b)，(B, a)，(B, b)，(C, a)，(C, b)，(D, a)，(D, b)，
∴ 这两人的成绩一个位于[80, 90)，一个位于[90, 100]的概率p＝．
【答案】
（1）由题意设圆C的标准方程为x2+(y−b)2＝r2，
则，解得．
∴ 圆C的标准方程为x2+(y−1)2＝1；
（2）圆C的圆心为(0, 1)，半径r＝1，
由圆的性质可知SPACB＝2S△PBC，
又四边形PACB的最小面积为2，则S△PBC的最小值为1，
即（d是切线长），∴ 切线长的最小值为2，
则圆心到直线kx+y+4＝0的距离为，
解得k＝2(k>0)．
【考点】
圆的标准方程
直线与圆的位置关系
【解析】
(Ⅰ)由题意设出圆C的标准方程为x2+(y−b)2＝r2，把点的坐标代入，可得关于b与r的方程组，求得b与r的值，则圆的方程可求；
(Ⅱ)由四边形PACB的最小面积是2求出圆心到直线的距离，再由点到直线的距离公式列式求得k值．
【解答】
（1）由题意设圆C的标准方程为x2+(y−b)2＝r2，
则，解得．
∴ 圆C的标准方程为x2+(y−1)2＝1；
（2）圆C的圆心为(0, 1)，半径r＝1，
由圆的性质可知SPACB＝2S△PBC，
又四边形PACB的最小面积为2，则S△PBC的最小值为1，
即（d是切线长），∴ 切线长的最小值为2，
则圆心到直线kx+y+4＝0的距离为，
解得k＝2(k>0)．
【答案】
（1）证明：取AC的中点F，连接PF，
∵ P、F分别为AE，∴ PF // CE，
同理可得，QF // AB // DE，
∵ PF∩QF＝F，PF，CE∩DE＝E、DE⊂平面CDE，
∴ 平面PQF // 平面CDE，
∵ PQ⊂平面PQF，
∴ PQ // 平面CDE．
（2）设AC＝1，则AB＝，
∵ 平面ABDE⊥平面ABC，平面ABDE∩平面ABC＝AB，
∴ AC⊥平面ABDE，∴ AC⊥AE，
∵ AE＝AB＝，∴ CE＝，
∵ 平面ABDE⊥平面ABC，平面ABDE∩平面ABC＝AB，
∴ BD⊥平面ABC，∴ CD＝＝，
∴ DE2+CE2＝CD2，即CE⊥DE，又AE⊥DE，
∴ ∠AEC即为平面ABDE与平面CDE所成锐二面角，
在Rt△ACE中，AC＝6，∴ ∠ACE＝，
故平面ABDE与平面CDE所成锐二面角的大小为．
【考点】
二面角的平面角及求法
直线与平面平行
【解析】
此题暂无解析
【解答】
此题暂无解答年份代码t
1
2
3
4
5
年销售量y（万套）
5.6
5.7
6
6.2
6.5