江西省新余市2020-2021学年高一下学期期末数学（文）试题

这是一份江西省新余市2020-2021学年高一下学期期末数学（文）试题，文件包含江西省新余市2020-2021学年高一下学期期末数学文试题原卷版doc、江西省新余市2020-2021学年高一下学期期末数学文试题解析版doc等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

一､选择题：(本大题12小题，每小题5分，共60分.在每小题给出的四个选项中只有一项是符合题目要求的)
1. 与角终边位置相同的角是（ ）
A. 240°B. 60°C. 150°D. 480°
2. 已知向量，，，若为实数满足，则（ ）
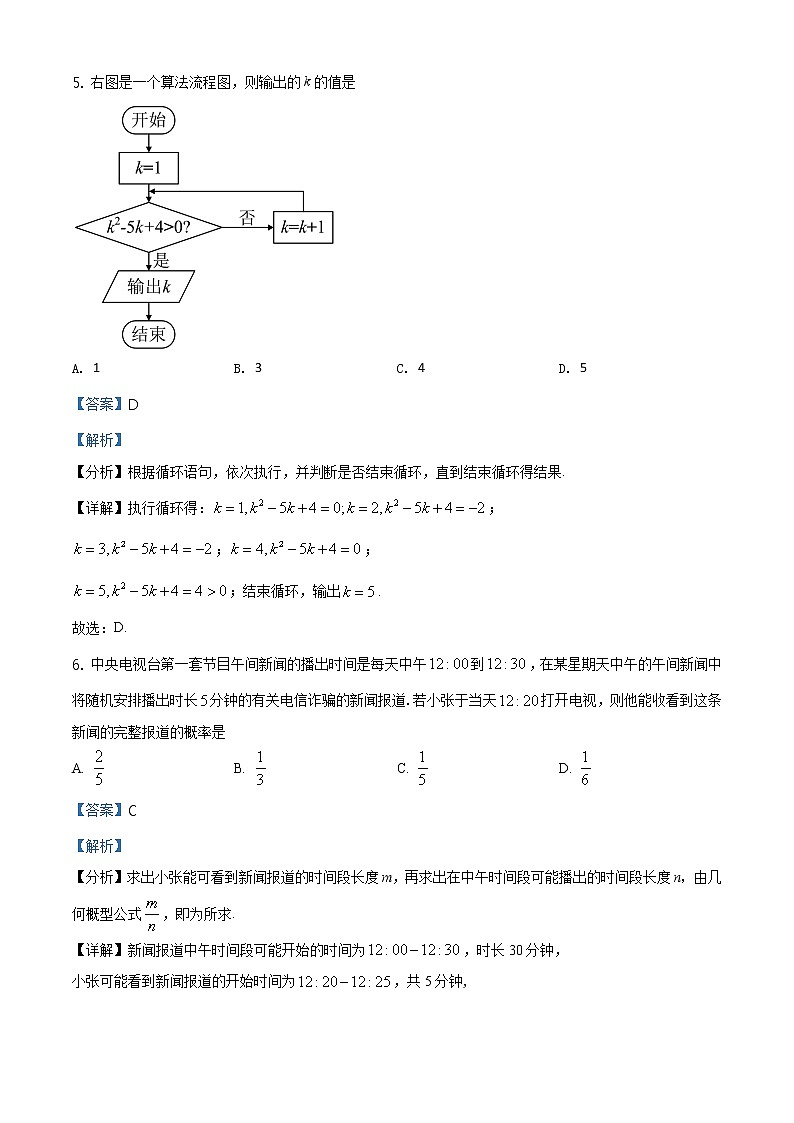
A. B. C. 1D. 2
3. 某市教体局对全市高一年级的学生身高进行抽样调查，随机抽取了100名学生，他们的身高都处在A，B，C，D，E五个层次内，根据抽样结果得到统计图表，则样本中B层人数是（ ）
A. 12B. 24C. 32D. 36
4. 在中，已知，那么一定是（ ）
A. 等腰三角形B. 直角三角形
C. 等边三角形D. 形状无法确定
5. 右图是一个算法流程图，则输出的k的值是
A. 1B. 3C. 4D. 5
6. 中央电视台第一套节目午间新闻的播出时间是每天中午到，在某星期天中午的午间新闻中将随机安排播出时长分钟的有关电信诈骗的新闻报道.若小张于当天打开电视，则他能收看到这条新闻的完整报道的概率是
A. B. C. D.
7. 锐角，满足，，那么
A. B. C. D.
8. 在等腰三角形中，，，若P为边上动点，则（ ）
A. 4B. 8C. D.
9. 已知定义域是，则的定义域为（ ）
A. ，B. ，
C. ，D. ，
10. 已知函数的部分图象如图所示，且，则（ ）
A. B. C. D.
11. 点在直线上，则实数取值范围是
A. B.
C. D.
12. 已知函数的图象关于直线对称，且对任意，都有，则当取最小值时，下列结论正确的是（ ）
A. 函数图象的一个对称中心为点
B. 函数图象的一条对称轴方程为
C. 将函数的图象向右平移个单位长度后得到函数的图象
D. 函数在上单调递减
二､填空题(本大题共4小题，每小题5分，共20分)
13. 若扇形的中心角为，半径为，则此扇形的面积为___________.
14. 已知定义在R上的偶函数满足，当时，，则___________.
15. 求值_______.
16. 如图所示，A，B，C是圆O上的三点，线段的延长线与的延长线交于圆O外的一点D，若，则的取值范围是___________.
三､解答题(本大题共6小题，共70分，解答应写出必要的文字说明，证明过程或演算步骤)
17. 已知，
（1）若，求的坐标；
（2）若与夹角为120°，求.
18. 已知，且.
（1）由的值；
（2）求的值.
19. 某5G科技公司对某款5G产品在2020年1月至6月的月销售量及月销售单价进行了调查，月销售单价x和月销售量y之间的一组数据如表所示：
（1）由散点图可知变量y与x具有线性相关关系，根据1月至6月的数据，求出y关于x的回归直线方程；
（2）预计在今后的销售中，月销售量与月销售单价仍然服从（1）中的关系，若该种产品的成本是350元/件，则该产品的月销售单价应定为多少元才能获得最大月利润？(注：利润=销售收入-成本)
参考公式和部分数据：，.
20. 2021年，是中国共产党建党百年华诞.为迎接建党100周年，某单位组织全体党员开展“学党史，知党情，感党恩”系列活动.在学党史知识竞赛中，共设置20个小题，每个小题5分.随机对100名党员的成绩进行统计，成绩均在内，现将成绩分成5组，按照下面分组进行统计分析：第1组，第2组，第3组，第4组，第5组，并绘制成如图所示的频率分布直方图.已知甲､乙､丙分别在第3，4，5组，现在用分层抽样的方法在第3，4，5组共选取6人（包含甲､乙､丙）参加党史知识抢答赛.
（1）求这100人的平均得分(同一组数据用该区间的中点值作代表)；
（2）求第4组选取参加抢答赛的人数；
（3）若从参加抢答赛的6人中随机选取两人参加上级部门的党史知识复赛，求甲､乙､丙3人至多有一人被选取的概率.
21. 已知函数．
（1）请用“五点法”列表并画出函数在一个周期上的图象；
（2）若方程在上有解，求实数a的取值范围；
（3）若函数的图象横坐标变为原来的2倍，纵坐标不变，再向右平移个单位得到函数的图象，求的单调增区间．
22. 已知，.其中.设函数，如图是函数在一个周期内的图象，A为图象的最高点，B，C为图象与x轴的交点，为等边三角形.将函数的图象上各点的横坐标变为原来的倍后，再向右平移个单位，向上平移1个单位，得到函数的图象.
（1）求函数的解析式；
（2）若不等式对任意恒成立，求实数m的取值范围.
月份
1
2
3
4
5
6
月销售单价x(百元)
9
8.8
8.6
8.4
8.2
8
月销售量y(万件)
68
75
80
83
84
90