

2020-2021学年江苏省扬州市高一(上)1月月考数学试卷苏教版
展开1. 若csα−π2=12,则sin(π+α)=( )
A.−32B.−12C.32D.12
2. 已知实数a,b,c,满足a=lg35,3b=4,3c=3,则a,b,c的大小关系正确的是( )
A.b
3. 已知函数f(x)=sinπx6,x≤0,lg13x,x>0,则f(f(9))=( )
A.12B.−12C.−32D.32
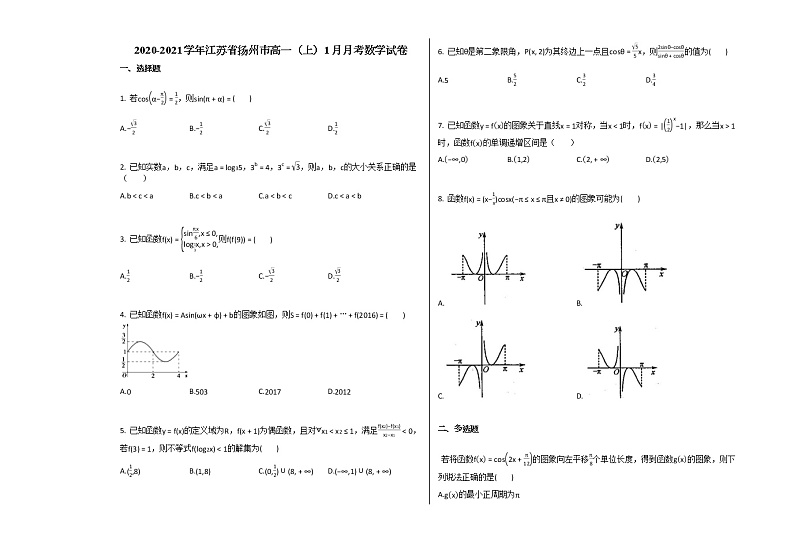
4. 已知函数f(x)=Asin(ωx+φ)+b的图象如图,则S=f(0)+f(1)+⋯+f(2016)=( )
A.0B.503C.2017D.2012
5. 已知函数y=f(x)的定义域为R,f(x+1)为偶函数,且对∀x1
6. 已知θ是第二象限角,P(x, 2)为其终边上一点且csθ=55x,则2sinθ−csθsinθ+csθ的值为( )
A.5B.52C.32D.34
7. 已知函数y=fx的图象关于直线x=1对称,当x<1时,fx=|12x−1|,那么当x>1时,函数fx的单调递增区间是( )
A.−∞,0B.1,2C.2,+∞D.2,5
8. 函数f(x)=(x−1x)csx(−π≤x≤π且x≠0)的图象可能为( )
A.B.
C.D.
二、多选题
若将函数fx=cs2x+π12的图象向左平移π8个单位长度,得到函数gx的图象,则下列说法正确的是( )
A.gx的最小正周期为π
B.gx在区间0,π2上单调递减
C.x=π12不是函数gx图象的对称轴
D.gx在−π6,π6上的最小值为−12
在平面直角坐标系中,横、纵坐标均为整数的点为整点,若函数fx的图象恰好通过nn∈N∗个整点,则称函数fx为n阶整点函数,则下列函数是一阶整点函数的是( )
A.fx=sinxB.gx=x2C.ℎx=12xD.φx=lnx
下列结论正确的是( )
A.若函数f2x的定义域为1,2,则函数fx的定义域是2,4
B.函数fx=ax−1+lga2x−1−1(其中a>0,且a≠1)的图象过定点1,0
C.当α=0时,幂函数y=xα的图象是一条直线
D.若lga12>1,则a的取值范围是12,1
关于函数f(x)=cs|x|+|csx|,下列结论正确的是( )
A.f(x)为偶函数B.f(x)在区间(−π2,0)上单调递增
C.f(x)的最大值为2D.f(x)在[−π,π]上有4个零点
三、填空题
《九章算术》是我国古代数学名著,其中有这样一个问题:“今有宛田,下周三十步,径十六步,问为田几何?”意思说:现有扇形田,弧长三十步,直径十六步,问面积多少?书中给出计算方法:以径乘周,四而一,即扇形的面积等于直径乘以弧长再除以4.在此问题中,扇形的圆心角的弧度数是________.
函数y=lg2(−x2+4x)的增区间是________,值域是________.
对任意的θ∈(0, π2),不等式1sin2θ+4cs2θ≥|2x−1|恒成立,则实数x的取值范围是________.
设函数fx的定义域为D,若满足:①fx在D内是单调函数;②存在m2,n2⊆D,使得fx在m2,n2上的值域为m,n,那么就称函数fx为“梦想函数”,若函数fx=lgaax+ta>0,a≠1是“梦想函数”,则t的取值范围是________.
四、解答题
已知α∈(0, π),且sin(7π2−α)+cs(5π2+α)=55.
(1)求csα1+sinα1−sinα+sinα1+csα1−csα的值;
(2)求sin3α−5csα4sinα+2cs3α的值.
已知函数y=ax(a>0且a≠1)在区间[1, 2]上的最大值与最小值之和为20,记f(x)=axax+2.
(1)求a的值;
(2)证明:f(x)+f(1−x)=1;
(3)求f(12017)+f(22017)+f(32017)+⋯+f(20162017)的值.
在①函数f(x−π3)为奇函数;②当x=π3时,f(x)=3;③2π3是函数f(x)的一个零点这三个条件中任选一个,补充在下面问题中,并解答:
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π2),f(x)的图象相邻两条对称轴之间的距离为π,________.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[0, 2π]上的单调递增区间.
已知函数fx=Asinωx+φ+BA>0,ω>0,|φ|<π2的一系列对应值如下表:
(1)根据表格提供的数据求函数fx的一个解析式;
(2)根据(1)的结果,若函数y=f(kx)(k>0)的最小正周期为2π3,当x∈0,π3时,方程fkx=m恰有两个不同的解,求实数m的取值范围.
已知指数函数fx=3x.
(1)若函数g(x) = f(x) − 1f(x) + 1,求函数g(x)值域,证明函数g(x)在定义域上单调递增;
(2)若函数ℎx=af(x)+bf(−x)(a, b∈R),研究ℎ(x)的奇偶性;
(3)若不等式f(2x)−(t+2)f(x)≥3−t在x∈[1, 2]上恒成立,求实数t的取值范围.
已知偶函数fx=lg22x+1−kx.
(1)若方程fx+12x+1fx+12x−1=aa∈R有两不等实根,求a的取值范围;
(2)若gx=2x+2−x−2b⋅2f(x)+b2b∈R在0≤x≤2上的最小值为2,求6的值.
参考答案与试题解析
2020-2021学年江苏省扬州市高一(上)1月月考数学试卷
一、选择题
1.
【答案】
B
【考点】
诱导公式
【解析】
本题考查三角函数的化简求值.根据诱导公式可知csα−π2=csπ2−α=sinα=12 ,再利用诱导公式即可求解sinπ+α=−sinα=−12 .
【解答】
解:因为csα−π2=csπ2−α=sinα=12 ,
所以sinπ+α=−sinα=−12 .
故选B.
2.
【答案】
B
【考点】
对数值大小的比较
指数式与对数式的互化
【解析】
由题意可得出b=lg34,c=lg33,然后根据对数函数y=lg3x的单调性即可得出a,b,c的大小关系.
【解答】
解:由题意可得出a=lg35,b=lg34,c=lg33,
又∵ lg33
3.
【答案】
C
【考点】
函数的求值
【解析】
此题暂无解析
【解答】
解:∵ 函数f(x)=sinπx6,x≤0,lg13x,x>0,
∴ f(9)=lg139=−2,
∴ f(f(9))=f(−2)=sin−2π6=−sinπ3=−32.
故选C.
4.
【答案】
C
【考点】
由y=Asin(ωx+φ)的部分图象确定其解析式
函数的求值
【解析】
由题意可得A和b值,再由周期性可得ω,代点可得φ值,可得解析式,计算可得f(0),f(1),f(2),f(3),由周期性可得.
【解答】
解:由图象知A=12,b=1,函数的周期T=4,
由周期公式可得ω=2πT=π2,
∴ f(x)=12sin(π2x+φ)+1,
当x=0时,f(0)=12sinφ+1=1,
∴ φ=2kπ(k∈Z),故f(x)=12sinπ2x+1,
∵ f(0)=1,f(1)=32,f(2)=1,f(3)=12,
∴ f(0)+f(1)+f(2)+f(3)=4,
∴ f(0)+f(1)+f(2)+...+f(2016)=504×4+f(0)=2017.
故选C.
5.
【答案】
A
【考点】
函数的对称性
函数单调性的性质
函数单调性的判断与证明
【解析】
f(x+1)为R上的偶函数,可得f(−r+1)=f(r+1),即函数f(r)关于直线x=1对称.对∀x1
解:∵ fx+1为R上的偶函数,
∴ f−x+1=fx+1,
∴ 函数fx关于直线x=1对称.
对∀x1
若f3=1,则不等式flg2x<1⇒flg2x
解得:12
故选A.
6.
【答案】
A
【考点】
任意角的三角函数
同角三角函数间的基本关系
三角函数线
【解析】
(Ⅰ)由题意利用任意角的三角函数的定义求得x的值,再利用同角三角函数的基本关系,求得要求式子的值.
(Ⅱ)由题意利用诱导公式、同角三角函数的基本关系,求得α,β的值.
【解答】
解:已知θ是第二象限角,P(x, 2)为其终边上一点,
且csθ=55x=xx2+4,
∵ x<0,
∴ x=−1,
∴ tanθ=2x=−2,
∴ 2sinθ−csθsinθ+csθ=2tanθ−1tanθ+1=5.
故选A.
7.
【答案】
C
【考点】
函数的单调性及单调区间
函数的对称性
【解析】
由题意可得可将x换为2−x,可得x>1的fx的解析式,画出图象,即可得到所求递增区间.
【解答】
解:∵ 函数y=fx的图象关于直线x=1对称,
当x<1时,fx=|12x−1|,
∴ x>1时,fx=|122−x−1|,
即为fx=|2x−2−1|,
画出y=fx的图象,
由图象可知:当x>1时,函数的递增区间为2,+∞.
故选C.
8.
【答案】
D
【考点】
函数的图象
【解析】
此题暂无解析
【解答】
解:f(−x)=(−x+1x)cs(−x)
=−(x−1x)csx
=−f(x),
∴ 所以函数f(x)为奇函数,排除A,B,
∵ f(π)=−(π−1π)<0,故排除C.
故选D.
二、多选题
【答案】
A,C,D
【考点】
余弦函数的周期性
函数y=Asin(ωx+φ)的图象变换
余弦函数的对称性
余弦函数的单调性
余弦函数的定义域和值域
【解析】
由函数图象的变换可得gx=cs2x+π3,结合余弦函数的周期性、单调性、对称轴等即可判断选项,得出答案.
【解答】
解:∵ gx=cs2x+π8+π12=cs2x+π3,
∴ gx的最小正周期为π,选项A正确;
当x∈0,π2时,2x+π3∈π3,4π3,
故gx在0,π2上有增有减,选项B错误;
gπ12=0,故x=π12不是gx图象的一条对称轴,选项C正确;
当x∈−π6,π6时,2x+π3∈0,2π3,
且当2x+π3=2π3,即x=π6时,gx取最小值−12,选项D正确.
故选ACD.
【答案】
A,D
【考点】
函数新定义问题
函数的图象
【解析】
本题考查新定义的一阶整点函数,考查三角函数,指数函数,对数函数即幂函数的图象和性质,
对给出的四个函数图象逐个分析,可得出答案.
【解答】
解:A,fx=sinx,其图象只经过一个整点,即0,0,故A正确;
B,gx=x2经过整点0,0,1,1,⋯,故不是一阶整点函数,故B错误;
C,ℎx=12x的图象经过整点−1,2,0,1,⋯,故不是一阶整点函数,故C错误;
D,φx=lnx的图象只经过一个整点1,0,故D正确.
故选AD.
【答案】
A,B,D
【考点】
对数函数的图象与性质
幂函数的图像
函数的定义域及其求法
对数函数图象与性质的综合应用
【解析】
A.考查复合函数的定义域问题;
B.考查指数函数和对数函数过定点问题;
C.考查幂函数的图象和性质;
D.考查对数函数的单调性问题.
【解答】
解:A,函数f2x的定义域为1,2,则1≤x≤2,所以2≤2x≤22=4,
故函数fx的定义域为2,4,故A正确;
B,因为a0=1,lga1=0,a>0且a≠1,
故x=1时,f1=a0+lga1−1=1−1=0,故B正确;
C,α=0时,y=x0,其定义域为xx≠0,故其图象为一条直线去掉点0,0,故C错误;
D,lga12>1=lgaa,当a>1时,lga12<0,不等式不成立,舍,
当0
【答案】
A,B,C
【考点】
复合三角函数的单调性
函数奇偶性的判断
函数的零点
三角函数的最值
【解析】
此题暂无解析
【解答】
解:A,f(−x)=cs|−x|+|cs(−x)|=cs|x|+|csx|=f(x),
∴ f(x)是偶函数,故A正确;
B,当x∈(−π2,0)时,f(x)=csx+csx=2csx,
此时f(x)在(−π2,0)上单调递增,故B正确;
C,当x>0时,f(x)=csx+|csx|≤|csx|+|csx|≤2,
当x=2kπ(k≥0,k∈Z)时等号成立.
又∵ f(x)是偶函数,∴ f(x)的最大值为2,故C正确;
D,当x∈[π2,π]时,f(x)=csx−csx=0,此时函数有无数个零点,故D错误.
故选ABC.
三、填空题
【答案】
154
【考点】
弧度制
弧长公式
【解析】
根据题意知扇形的弧长和直径,再计算扇形的面积和圆心角弧度数.
【解答】
解:扇形中,弧长为l=30,直径为d=16,则半径r=8,
扇形的圆心角弧度数是α=lr=308=154.
故答案为:154.
【答案】
(0, 2],(−∞, 2]
【考点】
复合函数的单调性
函数的单调性及单调区间
函数的值域及其求法
【解析】
由题意利用复合函数的单调性,可得本题即求函数t=−x2+4x在满足t>0的条件下,函数t的增区间,再利用二次函数的性质可得结论;求出t的范围,可得y的范围.
【解答】
解:函数y=lg2(−x2+4x)的增区间,即函数t=−x2+4x在满足t>0的条件下,函数t的增区间,
再利用二次函数的性质可得在满足t>0的条件下,函数t的增区间为(0, 2].
由于0
【答案】
[−4, 5]
【考点】
基本不等式在最值问题中的应用
同角三角函数间的基本关系
【解析】
θ∈(0, π2),可得1sin2θ+4cs2θ=(sin2θ+cs2θ)(1sin2θ+4cs2θ)=5+(4tan2θ+1tan2θ),利用基本不等式的性质可得出最小值.根据对任意的θ∈(0, π2),不等式1sin2θ+4cs2θ≥|2x−1|恒成立,可得|2x−1|≤(1sin2θ+4cs2θ)min,即可得出.
【解答】
解:∵ θ∈(0, π2)
∴ 1sin2θ+4cs2θ
=(sin2θ+cs2θ)(1sin2θ+4cs2θ)
=5+(4tan2θ+1tan2θ)
≥5+24tan2θ×1tan2θ=9,
当且仅当tanθ=22时取等号.
∵ 对任意的θ∈(0, π2),不等式1sin2θ+4cs2θ≥|2x−1|恒成立,
∴ |2x−1|=9.
∴ −9≤2x−1≤9,
解得−4≤x≤5.
∴ 实数x的取值范围是[−4, 5].
故答案为:[−4, 5].
【答案】
(−14,0)
【考点】
复合函数的单调性
函数的值域及其求法
【解析】
由题意可得,函数fx=lgaax+ta>0,a≠1在定义域上为增函数,则lgaam2+t=m,lgaan2+t=n,即am=am2+t,an=an2+t,即ax22−ax2−t=0有两个不同的正数解,进而求得t的取值范围.
【解答】
解:由复合函数的单调性可知,
函数fx=lgaax+t a>0,a≠1在定义域上为增函数,
结合“希望函数”的定义可知,
lgaam2+t=m,lgaan2+t=n,
即am=am2+t,an=an2+t,
所以ax=ax2+t有两个不同的正数解,
即ax22−ax2−t=0有两个不同的正数解,
所以Δ=1+4t>0,且−t>0,
解得:−14
四、解答题
【答案】
解:1∵ α∈(0, π),且sin(7π2α)+cs(5π2+α)=55,
∴ 可得:−csα−sinα=55,即csα+sinα=55,
两边平方可得:1+2csαsinα=15,可得2csαsinα=−45,
∴ α为钝角,csα<0,
∴ csα1+sinα1−sinα+sinα1+csα1−csα
=csα(1+sinα)2cs2α+sinα(1+csα)2sin2α
=−(1+sinα)+1+csα
=csα−sinα
=(csα−sinα)2
=1(45)=355.
(2)∵ 由(1)可得:α∈(0, π),csα+sinα=−55<0①,
∴ α∈(π2, π),
又∵ cs2α+sin2α=1②,
∴ 由①②解得csα=−255,sinα=55,
∴ sin3α−5csα4sinα+2cs3α=525+25455−16525=514.
【考点】
运用诱导公式化简求值
三角函数的恒等变换及化简求值
【解析】
(1)由已知利用诱导公式可求csα+sinα = − 55,两边平方可得2csαsinα = − 45,进而利用同角三角函数基本关系式化简所求即可得解.
(2)由(1)可得csα+sinα = − 55,结合角的范围利用同角三角函数基本关系式可求csα,sinα的值,即可计算得解.
【解答】
解:1∵ α∈(0, π),且sin(7π2α)+cs(5π2+α)=55,
∴ 可得:−csα−sinα=55,即csα+sinα=55,
两边平方可得:1+2csαsinα=15,可得2csαsinα=−45,
∴ α为钝角,csα<0,
∴ csα1+sinα1−sinα+sinα1+csα1−csα
=csα(1+sinα)2cs2α+sinα(1+csα)2sin2α
=−(1+sinα)+1+csα
=csα−sinα
=(csα−sinα)2
=1(45)=355.
(2)∵ 由(1)可得:α∈(0, π),csα+sinα=−55<0①,
∴ α∈(π2, π),
又∵ cs2α+sin2α=1②,
∴ 由①②解得csα=−255,sinα=55,
∴ sin3α−5csα4sinα+2cs3α=525+25455−16525=514.
【答案】
(1)解:由题得a1+a2=20,解得a=4,a=−5(舍),所以a=4.
(2)证明:由(1)知f(x) = 4x4x + 2,
所以f(x)+f(1−x) = 4x4x + 2 + 41 − x41 − x + 2
= 4x4x + 2 + 44x44x + 2 = 4x4x + 2 + 42 × 4x + 4
= 4x4x + 2 + 24x + 2 = 1.
(3)解:由(2)知f(12017)+f(20162017)=1,f(22017)+f(20152017)=1,⋯,f(10082017)+f(10092017)=1,
所以f(12017)+f(22017)+f(32017)+⋯+f(20152017)+f(20162017)
=[f(12017)+f(20162017)]+[f(22017)+f(20152017)]
+⋯+[f(10082017)+f(10092017)]
=1+1+1+⋯+1=1008.
【考点】
函数最值的应用
函数的求值
【解析】
(1)根据指数函数是单调函数可得最大值与最小值和为a1+a2=20,解得a=4;
(2)根据条件求出f(x) = 4x4x + 2,可得f(x)+f(1−x)=1;
(3)由(2)可知f(12017)+f(20162017)=1,f(22017)+f(20152017)=1,…,f(10082017)+f(10092017)=1,则原式=1008.
【解答】
(1)解:由题得a1+a2=20,解得a=4,a=−5(舍),所以a=4.
(2)证明:由(1)知f(x) = 4x4x + 2,
所以f(x)+f(1−x) = 4x4x + 2 + 41 − x41 − x + 2
= 4x4x + 2 + 44x44x + 2 = 4x4x + 2 + 42 × 4x + 4
= 4x4x + 2 + 24x + 2 = 1.
(3)解:由(2)知f(12017)+f(20162017)=1,f(22017)+f(20152017)=1,⋯,f(10082017)+f(10092017)=1,
所以f(12017)+f(22017)+f(32017)+⋯+f(20152017)+f(20162017)
=[f(12017)+f(20162017)]+[f(22017)+f(20152017)]
+⋯+[f(10082017)+f(10092017)]
=1+1+1+⋯+1=1008.
【答案】
解:1∵ f(x)的图象相邻两条对称轴之间的距离为π,
∴ T=2πω=2π,∴ ω=1,
∴ f(x)=2sin(x+φ).
选择①:∵ 函数f(x−π3)=2sin(x+φ−π3)为奇函数,
∴ f(−π3)=2sin(φ−π3)=0,解得φ=π3+kπ,k∈Z.
∵ 0< φ< π2,
∴ φ = π3,
∴ f(x) = 2sin(x + π3).
选择②:∵ f(π3)=2sin(π3+φ)=3,
∴ sin(π3+φ)=32,
∴ φ=2kπ,k∈Z或φ=π3+2kπ,k∈Z.
∵ 0< φ< π2,
∴ φ = π3,
∴ f(x) = 2sin(x + π3).
选择③:∵ 2π3是函数f(x)的一个零点,
∴ f(2π3)=2sin(2π3+φ)=0,
∴ φ=kπ−2π3,k∈Z.
∵ 0< φ< π2,
∴ φ = π3,
∴ f(x) = 2sin(x + π3).
2由−π2+2kπ≤x+π3≤π2+2kπ,k∈Z,
得−56π+2kπ≤x≤π6+2kπ,k∈Z,
∴ 令k=0,得 − 5π6 ≤ x ≤ π6,
令k=1,得7π6 ≤ x ≤ 13π6,
∴ 函数f(x)在[0, 2π]上的单调递增区间为[ 0,π6] ,[ 76π,2π] .
【考点】
由y=Asin(ωx+φ)的部分图象确定其解析式
正弦函数的单调性
【解析】
1 根据φ的范围确定φ的取值,然后函数解析式即可确定.
2方案一:由题意可求函数周期,利用周期公式可求ω,选条件①由题意可得φ = π3 + kπ,k∈Z,结合范围0< φ< π2,可求φ = π3,可得函数解析式,利用正弦函数的单调性可求函数f(x)在[0, 2π]上的单调递增区间;
方案二:选条件②,由题意可得sin(π3 + φ) = 32,可求φ,求解函数解析式,利用正弦函数的单调性可求函数f(x)在[0, 2π]上的单调递增区间;
方案三:选条件③,由题意可得f(23π) = 2sin(23π + φ) = 0,求得φ = kπ − 2π3,k∈Z,可求φ,求解函数解析式,利用正弦函数的单调性可求函数f(x)在[0, 2π]上的单调递增区间.
【解答】
解:1∵ f(x)的图象相邻两条对称轴之间的距离为π,
∴ T=2πω=2π,∴ ω=1,
∴ f(x)=2sin(x+φ).
选择①:∵ 函数f(x−π3)=2sin(x+φ−π3)为奇函数,
∴ f(−π3)=2sin(φ−π3)=0,解得φ=π3+kπ,k∈Z.
∵ 0< φ< π2,
∴ φ = π3,
∴ f(x) = 2sin(x + π3).
选择②:∵ f(π3)=2sin(π3+φ)=3,
∴ sin(π3+φ)=32,
∴ φ=2kπ,k∈Z或φ=π3+2kπ,k∈Z.
∵ 0< φ< π2,
∴ φ = π3,
∴ f(x) = 2sin(x + π3).
选择③:∵ 2π3是函数f(x)的一个零点,
∴ f(2π3)=2sin(2π3+φ)=0,
∴ φ=kπ−2π3,k∈Z.
∵ 0< φ< π2,
∴ φ = π3,
∴ f(x) = 2sin(x + π3).
2由−π2+2kπ≤x+π3≤π2+2kπ,k∈Z,
得−56π+2kπ≤x≤π6+2kπ,k∈Z,
∴ 令k=0,得 − 5π6 ≤ x ≤ π6,
令k=1,得7π6 ≤ x ≤ 13π6,
∴ 函数f(x)在[0, 2π]上的单调递增区间为[ 0,π6] ,[ 76π,2π] .
【答案】
解:(1)设f(x)的最小正周期为T,得T=11π6−(−π6)=2π,
由T=2πω,得ω=1,
又B+A=3,B−A=−1, 解得A=2,B=1,
根据|φ|<π2,
令ω⋅5π6+φ=π2,
即5π6+φ=π2,解得φ=−π3,
∴ f(x)=2sin(x−π3)+1.
(2)∵ 函数y=f(kx)=2sin(kx−π3)+1的最小正周期为2π3,
又k>0,∴ k=3,
令t=3x−π3,∵ x∈[0,π3],∴ t∈[−π3,2π3],
如图,sint=s在[−π3,2π3]上有两个不同的解,
则s∈[32,1),
∴ 方程f(kx)=m在x∈[0,π3]时恰好有两个不同的解,则m∈[3+1,3),
即实数m的取值范围是[3+1,3).
【考点】
由y=Asin(ωx+φ)的部分图象确定其解析式
根的存在性及根的个数判断
【解析】
此题暂无解析
【解答】
解:(1)设f(x)的最小正周期为T,得T=11π6−(−π6)=2π,
由T=2πω,得ω=1,
又B+A=3,B−A=−1, 解得A=2,B=1,
根据|φ|<π2,
令ω⋅5π6+φ=π2,
即5π6+φ=π2,解得φ=−π3,
∴ f(x)=2sin(x−π3)+1.
(2)∵ 函数y=f(kx)=2sin(kx−π3)+1的最小正周期为2π3,
又k>0,∴ k=3,
令t=3x−π3,∵ x∈[0,π3],∴ t∈[−π3,2π3],
如图,sint=s在[−π3,2π3]上有两个不同的解,
则s∈[32,1),
∴ 方程f(kx)=m在x∈[0,π3]时恰好有两个不同的解,则m∈[3+1,3),
即实数m的取值范围是[3+1,3).
【答案】
解:(1)由fx=3x,可得g(x) = 3x − 13x + 1 = 1 − 23x + 1,
由3x>0,可得3x+1>1,则−2< − 23x + 1< 0,
则−1<1 − 23x + 1< 1,
即g(x)的值域为(−1, 1).
证明:设x1,x2∈R,且x1
= 2⋅3x1 − 3x2(3x1 + 1)(3x2 + 1),
由x1
则g(x1)−g(x2)<0,即g(x1)
2 函数ℎx=af(x)+bf(−x)=a⋅3x+b⋅3−x,
ℎ−x=a⋅3−x+b⋅3x,
则ℎ(−x)+ℎ(x)=(a+b)(3x+3−x),ℎ(−x)−ℎ(x)=b−a3x−3−x,
当a=b=0时,ℎ(x)=0,ℎ(x)既是奇函数也是偶函数;
当a=−b≠0,ℎ(−x)=−ℎx,ℎ(x)是奇函数;
当a=b≠0,ℎ(−x)=ℎx,ℎ(x)是偶函数;
当a≠b且a≠−b,ℎ(x)是非奇非偶函数.
3不等式f(2x)−(t+2)f(x)≥3−t在x∈[1, 2]上恒成立,
即为32x−(t+2)⋅3x≥3−t在x∈[1, 2]上恒成立,
即t(3x−1)≤32x−2⋅3x−3在x∈[1, 2]上恒成立.
设m=3x−1(2≤m≤8),则t≤m2−4m=m−4m,
由y=m和y = − 4m在2≤m≤8递增,可得y=m − 4m在2≤m≤8递增,
可得m=2时,y=m − 4m取得最小值0,
则t≤0,可得t的取值范围是(−∞, 0].
【考点】
函数的值域及其求法
函数单调性的判断与证明
函数奇偶性的判断
函数恒成立问题
【解析】
(1)运用指数函数的值域和不等式的性质,可得g(x)的值域;再由单调性的定义,结合指数函数的单调性可证明g(x)的单调性;
(2)计算ℎ(x),ℎ(−x),结合奇偶性的定义,分别讨论a,b,即可得到ℎ(x)的奇偶性;
(3)由题意可得32x−(t+2)⋅3x≥3−t在x∈[1, 2]上恒成立,由参数分离和换元法、以及指数函数的单调性,不等式恒成立思想,可得所求范围.
【解答】
解:(1)由fx=3x,可得g(x) = 3x − 13x + 1 = 1 − 23x + 1,
由3x>0,可得3x+1>1,则−2< − 23x + 1< 0,
则−1<1 − 23x + 1< 1,
即g(x)的值域为(−1, 1).
证明:设x1,x2∈R,且x1
= 2⋅3x1 − 3x2(3x1 + 1)(3x2 + 1),
由x1
则g(x1)−g(x2)<0,即g(x1)
2 函数ℎx=af(x)+bf(−x)=a⋅3x+b⋅3−x,
ℎ−x=a⋅3−x+b⋅3x,
则ℎ(−x)+ℎ(x)=(a+b)(3x+3−x),ℎ(−x)−ℎ(x)=b−a3x−3−x,
当a=b=0时,ℎ(x)=0,ℎ(x)既是奇函数也是偶函数;
当a=−b≠0,ℎ(−x)=−ℎx,ℎ(x)是奇函数;
当a=b≠0,ℎ(−x)=ℎx,ℎ(x)是偶函数;
当a≠b且a≠−b,ℎ(x)是非奇非偶函数.
3不等式f(2x)−(t+2)f(x)≥3−t在x∈[1, 2]上恒成立,
即为32x−(t+2)⋅3x≥3−t在x∈[1, 2]上恒成立,
即t(3x−1)≤32x−2⋅3x−3在x∈[1, 2]上恒成立.
设m=3x−1(2≤m≤8),则t≤m2−4m=m−4m,
由y=m和y = − 4m在2≤m≤8递增,可得y=m − 4m在2≤m≤8递增,
可得m=2时,y=m − 4m取得最小值0,
则t≤0,可得t的取值范围是(−∞, 0].
【答案】
解:(1)因为2x+1>0,所以fx的定义域为R.
因为fx是偶函数,即lg2(2−x+1)+kx=lg2(2x+1)−kx,
所以lg22x+12−x+1=2kx,故lg22x=2kx,
所以x=2kx,即方程2k−1x=0的解为一切实数,
所以k=12,
因为f(x)+12x+1f(x)+12x−1=a(a∈R),且fx=lg22x+1−12x,
所以原方程转化为
[lg2(2x+1)+1]|lg2(2x+1)−1|=a,
令t=lg22x+1t>0,则
Ft=t+1|t−1|t>0,
所以Ft=−t2+1,0
当0
故当0
所以2f(x)=2x2+2−x2,
所以g(x)=2x+2−x−2b2x2+2−x2+b2.
令m=2x2,则1≤m≤2,
令ℎm=m+1m,设1≤m1
=1m2m1(m2−m1)(m2m1−1),
因为1≤m1
即ℎm在1,2上是增函数,所以2≤ℎm≤52,
设t=ℎm,则gt=t−b2−2.
①当b≤2时,gt的最小值为g2=2−b2−2,
所以2−b2−2=2,解得b=0,或b=4(舍去);
②当2
所以52−b2−2=2,解得b=92,或b=12(舍去).
综上知,b=0或b=92 .
【考点】
函数奇偶性的性质
函数单调性的性质
函数的零点与方程根的关系
函数的最值及其几何意义
二次函数在闭区间上的最值
【解析】
暂无
暂无
【解答】
解:(1)因为2x+1>0,所以fx的定义域为R.
因为fx是偶函数,即lg2(2−x+1)+kx=lg2(2x+1)−kx,
所以lg22x+12−x+1=2kx,故lg22x=2kx,
所以x=2kx,即方程2k−1x=0的解为一切实数,
所以k=12,
因为f(x)+12x+1f(x)+12x−1=a(a∈R),且fx=lg22x+1−12x,
所以原方程转化为
[lg2(2x+1)+1]|lg2(2x+1)−1|=a,
令t=lg22x+1t>0,则
Ft=t+1|t−1|t>0,
所以Ft=−t2+1,0
当0
故当0
所以2f(x)=2x2+2−x2,
所以g(x)=2x+2−x−2b2x2+2−x2+b2.
令m=2x2,则1≤m≤2,
令ℎm=m+1m,设1≤m1
=1m2m1(m2−m1)(m2m1−1),
因为1≤m1
即ℎm在1,2上是增函数,所以2≤ℎm≤52,
设t=ℎm,则gt=t−b2−2.
①当b≤2时,gt的最小值为g2=2−b2−2,
所以2−b2−2=2,解得b=0,或b=4(舍去);
②当2
所以52−b2−2=2,解得b=92,或b=12(舍去).
综上知,b=0或b=92 .
2020-2021学年江苏省扬州市仪征市高一(上)12月月考数学试卷苏教版: 这是一份2020-2021学年江苏省扬州市仪征市高一(上)12月月考数学试卷苏教版,共11页。试卷主要包含了选择题,多选题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年江苏省扬州市仪征市高一(上)10月月考考试数学试卷苏教版: 这是一份2020-2021学年江苏省扬州市仪征市高一(上)10月月考考试数学试卷苏教版,共9页。试卷主要包含了选择题,多选题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年江苏省扬州市高一(上)期末模拟考试数学试卷苏教版: 这是一份2020-2021学年江苏省扬州市高一(上)期末模拟考试数学试卷苏教版,共12页。试卷主要包含了选择题,多选题,填空题,解答题等内容,欢迎下载使用。












