高中数学北师大版 (2019)必修 第一册2.2 函数的表示法教学演示ppt课件

这是一份高中数学北师大版 (2019)必修 第一册2.2 函数的表示法教学演示ppt课件，共36页。PPT课件主要包含了思考交流，已知函数fx等内容，欢迎下载使用。

函数的概念？函数的三要素？
1，设A、B是非空数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应， 为从集合A到集合B的一个函数
2，三要素：定义域、值域、对应法则
例1．某种笔记本的单价是5元，买x (x∈{1，2，3，4，5})个笔记本需要y元．试用三种表示法表示函数y=f(x) ．
{1,2,3,4,5}
y=5x,x∈{1,2,3,4,5}
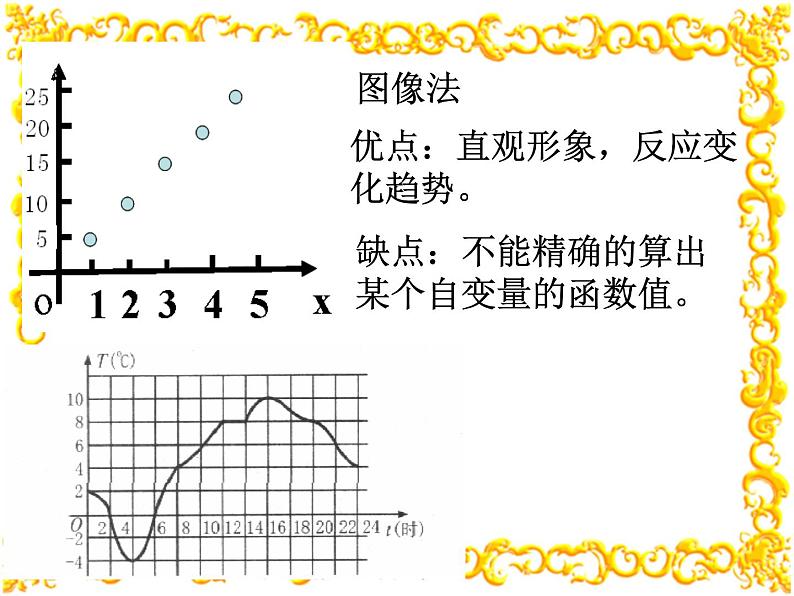
教学函数的三种表示方法：
解析式法、列表法、图像法
如：一天中温度随时间的变化
例1：用解析法表示为:
解析法：优点：简明；给自变量求函数值.
缺点：不是所有的函数都有解析式
列表法：优点：不需计算就可直接看出自变量相应的函数值。
缺点：对于自变量的有些取值，从表中得不到相应的函数值，另外因变量变化规律不明显。
优点：直观形象，反应变化趋势。
缺点：不能精确的算出某个自变量的函数值。
下表是某校高一（1）班三位同学在高一学年度六次数学测试的成绩及班级平均分表：
思考1:上表反映了几个函数关系？这些函数的自变量是什么？定义域是什么？
4个；测试序号；{1，2，3，4，5，6}.
思考2:上述4个函数能用解析法表示吗？能用图象法表示吗？
思考3:若分析、比较每位同学的成绩变化情况，用哪种表示法为宜？
思考4:试根据图象对这三位同学在高一学年度的数学学习情况做一个分析.
王伟同学的数学成绩始终高于班级平均水平，学习情况比较稳定而且成绩优秀；张城同学的数学成绩不稳定，总是在班级平均水平上下波动，而且波动幅度较大；赵磊同学的数学成绩低于班级平均水平，但他的成绩呈上升趋势，表明他的数学成绩在稳步提升.
1.设A=[0,2], B=[1,2], 在下列各图
中, 能表示f:A→B的函数
2.小强去上学，先跑步，后步行，如果y表示小强离学校的距离，x表示出发后的时间，则下列图像中符合小强走法的是（ ）
例2：画出函数y=|x|的图象。
小结：什么是分段函数？
在函数的定义内，对自变量x不同取值范围，有着不同的对应法则，这样的函数叫分段函数
例3：某市“招手即停”公共汽车的票价按下列规定制定：(1)5公里以内（含5公里），票价2元；（2）5公里以上，每增加5公里，票价增加1元（不足5公里的按5公里计算）如果某条线路的总里程为20公里请根据题意写出票价与里程之间的函数解析式，并画出函数图像
1. 分段函数是一个函数,不要把它误认为是“几个函数”;
2. 分段函数的定义域是各个部分定义域的并集，值域也是各个部分值域的并集。
这种在定义域的不同部分，有不同的对应法则的函数称为分段函数。
练习1. A.画出函数f(x)=|x-2|的图像。 B.画出函数f(x)=|x-2|+|x+1|的图像，并求值域。
解：将函数化为分段函数形式
画出他的图像，由图所示
函数的值域是{y|≥3}
求出函数f(x)=|x-2|+|x+1|的值域。
法二：|x-2|表示数轴上一动点x与2的距离。
所以y=|x-2|+|x+1|表示数轴上一动点x到-1，2的距离之和，由数轴易见：
综上：值域为{y|y≥3}或写成y∈[3,+∞)
2x+3, x＜－1,
x2, －1≤x＜1,
x－1, x≥1 .
（2）求f[f(－2)] ;
（3） 当f (x)=－7时,求x ;
（1）求f(-2),f(1),f(5)
解： （1） f{f[f(－2)]} = f{f[-1]}
= f{1}= 0
(2)若x＜－1 , 2x+3 ＜1，与f (x)=－7相符，由2x+3 =－7得x=-5易知其他二段均不符合f (x)=－7 。 故 x=-5
2.函数r=f(p)的图像如图所示。(1)函数r=f(p)的定义域是什么？(2)函数r=f(p)的值域是什么？ (3)r取何值时，只有唯一的p值与之对应
[-5,0] ∪[2,6)
[0,2) ∪(5,+∞)
3、用固定的速度向如下图形状的瓶子注水，则水面的高度h和时间t之间的关系是( )
(02年全国高考) 向高为H的水瓶中注水,若注满为止,注水量V与水深h 的函数关系如图所示,那么水瓶的形状是( )
1,举例初中已经学习过的一些对应，或者日常生活中的一些对应实例：
(1)对于任何一个实数a，数轴上都有唯一的点P和它对应；
(2)对于坐标平面内任何一个点A，都有唯一的有序实数对(x,y)和它对应；
(3)对于任意一个三角形，都有唯一确定的面积和它对应；
(4)某影院的某场电影的每一张电影票有唯一确定的座位与它对应；
2. 讨论：函数存在怎样的对应？其对应有何特点？
A集合中的任意一个x，在B中有唯一的个f(x)与之对应。
只不过A,B一定均为非空数集。
而映射可以是任何集合之间的对应。如：
定义：两个集合A与B间存在着对应关系f，而且对于A中的每一个元素x，B中总有唯一的一个元素y与它对应，就称这种对应为从A到B的映射，记作f:A→B.
强调:(1)A中的任意，B中的唯一。
A中的元素x称为原像，B中的对应元素 y称为x的像，记作： f:x → y.
(2)可以多对一，不可一对多
(3)A中不能剩余，B中可有剩余
例1：以下给出的对应是不是从A到B的映射？
③A={P | P是数轴上的点}，集合B=R，对应关系f:数轴上的点与它所代表的实数对应；
⑤集合A={三角形}，集合B={圆}；对应关系f：每一个三角形都对应它的内切圆；
⑥集合A={x|x是石碣中学的班级}， 集合B={x|x是石碣中学的学生}； 对应关系f：每个班级对应班里的学生。
练习、判断下列对应，是否是映射？
映射f:A→B,理解为以下同点：
①A中每个元素在B中必有唯一的像
②对A中不同的元素，在B中可以有相同的像。
③允许B中元素没有原像。
④A到B对应,可以一对一,多对一,但不能一对多.
定义：若映射f:A→B满足：
①A中每一个元素在B中都有唯一 的像与之对应；
②A中的不同元素的像不相同
③B中每一个元素都有原像
三、一一映射（一一对应）
函数是一个特殊的映射；2)函数是非空数集A到非空数集B的映射， 而对于映射，A和B不一定是数集.
你能说出函数与映射之间的异同吗?
练习：教材P.23第4题．
练习：24页：设集合A={a,b,c},B={0,1}.试问：从A到B的映射共有几个？
如图，动点P从边长为1的正方形ABCD的顶点A出发，顺次经过B、C、D,再回到A，设x表示P的行程，y表示PA的长。求y关于x的函数关系式。
分析：由题意，可分成P在AB上；P在BC上；P在CD上；P在DA上四段来考虑。