冀教版八年级上册第十二章 分式和分式方程12.4 分式方程教课内容课件ppt

这是一份冀教版八年级上册第十二章 分式和分式方程12.4 分式方程教课内容课件ppt，共20页。PPT课件主要包含了问题思考，分式方程，分式方程的解法，知识拓展，课堂小结等内容，欢迎下载使用。

小红家到学校的路程为38km.小红从家去学校总是先乘公共汽车,下车后再步行2km,才能到学校,路途所用时间是1h.已知公共汽车的速度是小红步行速度的9倍,求小红步行的速度.
(1)上述问题中有哪些等量关系?(2)根据你所发现的等量关系,设未知数并列出方程.(3)如果设小红步行的时间为xh,又应该怎么列方程?
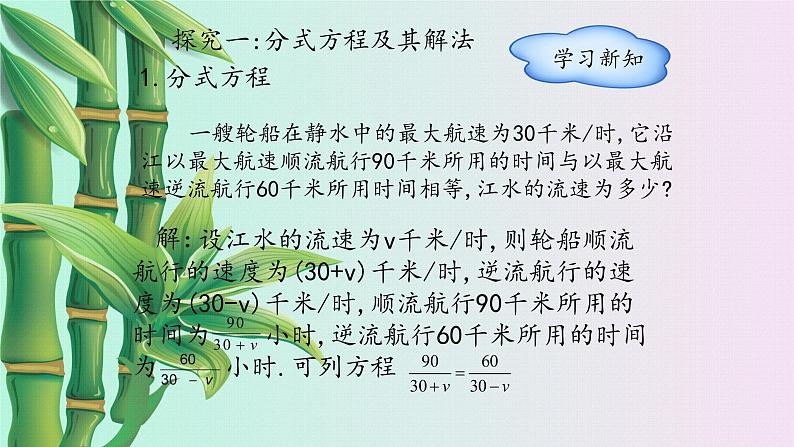
探究一:分式方程及其解法
　 一艘轮船在静水中的最大航速为30千米/时,它沿江以最大航速顺流航行90千米所用的时间与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?
【知识拓展】（1）理解分式方程要明确两点： ①是方程；②分母中含有未知数（也可以看作方程中含有分式）.（2）整式方程和分式方程统称为有理方程.
分母中含有未知数的方程叫做分式方程．
解分式方程的基本思路是将分式方程转化为整式方程,具体做法是“去分母”,即方程两边乘最简公分母,这是解分式方程的一般方法.
判断下列各式哪个是分式方程．
根据定义可得：（1）（2）是整式方程，（3）是分式，（4）（5）是分式方程．
解:两边同乘最简公分母2(x+5)得: 2(x+1)=5+x, 2x+2=5+x, x=3.
解:方程的两边同乘(30+v)(30-v), 得90(30-v)=60(30+v), 解得v=6.
如何解分式方程 ?
解分式方程的基本思想是将分式方程转化为整式方程,具体做法是“去分母”,即方程两边同乘最简公分母,这也是解分式方程的一般方法.
【拓展延伸】分式方程与整式方程的定义区分:
探究二:分式方程的增根
解:方程两边同乘x-1,得x+1=-(x-3)+(x-1), 解这个整式方程,得x=1.
在解分式方程时,通过去分母将分式方程转化为整式方程,并解这个整式方程,再将整式方程的根代入分式方程(或公分母)中检验. 当分母的值不等于0时,这个整式方程的根就是分式方程的根;当公分母的值为0时,分式方程无解,我们把这样的根叫做分式方程的增根.
方程两边同乘x+2,得2-(2-x)=3(x+2),解这个整式方程，得x=-3,经检验x=-3是分式方程的根。
(1)检验的方法有两种:①把未知数的值代入所乘最简公分母中,最简公分母为0是增根,舍去.最简公分母不为0的未知数的值就是原分式方程的解.②把未知数的值代入原方程,若左右两边的值相等,则这个未知数的值就是原方程的根;若某个分式的分母为0,则这个未知数的值就是增根,舍去.
(2)解分式方程时,必须注意以下几点:①若分式方程中的分母是多项式,应先对各分母因式分解,再寻求最简公分母;②将一个分式方程的两边同时乘最简公分母时,每一个式子都应乘到,不要漏乘,特别是不要漏乘没有分母的项;③解含字母系数的分式方程时,字母系数应视为具体数处理;④解分式方程时,检验这一步必不可少,它是解分式方程的一个重要步骤.
解分式方程的一般步骤:1.在方程的两边都乘最简公分母,约去分母,化为整式方程.2.解这个整式方程.3.把整式方程的根代入最简公分母,看结果是不是零;使最简公分母为零的根不是原方程的根,必须舍去.
解析:在方程的两边同乘最简公分母 变为整式方程为x(x+2)-(x-1)(x+2)=3,解得x =1,检验:当x=1时,(x-1)(x+2)=0,所以原分式方程无解.故选D.
解析:去分母得4x-12=3x-6,解得x=6,经检验x=6是分式方程的解.故填6.
解析:把方程的左右两边同时乘最简公分母,化成整式方程进行计算,注意检验.
解:(1)去分母,得3x+6-2x=0,解得x=-6.经检验,x=-6是原方程的解.
解析:增根是分式方程化为整式方程后产生的使分式方程的公分母为0的根.有增根,那么最简公分母3(x-2)=0,所以增根是x=2,把增根代入化为整式方程的方程即可求出m的值.