2019_2020学年苏州市石牌中学八上期末数学复习试卷（1）

这是一份2019_2020学年苏州市石牌中学八上期末数学复习试卷（1），共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是
A. B.
C. D.

2. 用直尺和圆规作一个角的平分线的示意图如图所示，则能说明 ∠AOC=∠BOC 的依据是
A. SSS
B. ASA
C. AAS
D. 角平分线上的点到角两边距离相等

3. 边长是 m 的正方形的面积是 7，如图，表示 m 的点在数轴上表示时，在哪两个字母之间
A. C 与 DB. A 与 BC. A 与 CD. B 与 C

4. 如果 m 是任意实数，则点 Pm−4,m+1 一定不在
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

5. 下列四幅图象近似刻画了两个变量之间的关系，图象与下列四种情景对应排序正确的是
①一辆汽车在公路上匀速行驶（汽车行驶的路程与时间的关系）；
②向锥形瓶中匀速注水（水面的高度与注水时间的关系）；
③将常温下的温度计插入一杯热水中（温度计的读数与时间的关系）；
④一杯越来越凉的水（水温与时间的关系）．
A. ①②④③B. ③④②①C. ①④②③D. ③②④①

6. 如图，直线 y=−x+2 与 y=ax+b（a≠0 且 a，b 为常数）的交点坐标为 3,−1，则关于 x 的不等式 −x+2≥ax+b 的解集为
A. x≥−1B. x≥3C. x≤−1D. x≤3

7. 等腰三角形的底边长为 6，底边上的中线长为 4，它的腰长为
A. 7B. 6C. 5D. 4

8. 在平面直角坐标系中，点 P−3,2 关于直线 y=x 的对称点的坐标是
A. −3,−2B. 2,−3C. 3,2D. 3,−2

9. 如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为 S1，S2，S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为 S4，S5，S6．其中 S1=16，S2=45，S5=11，S6=14 则 S3+S4=
A. 86B. 64C. 54D. 48

10. 如图，正方形 ABCD 的边长为 10，AG=CH=8，BG=DH=6，连接 GH，则线段 GH 的长为
A. 835B. 22C. 145D. 10−52

二、填空题（共10小题；共50分）
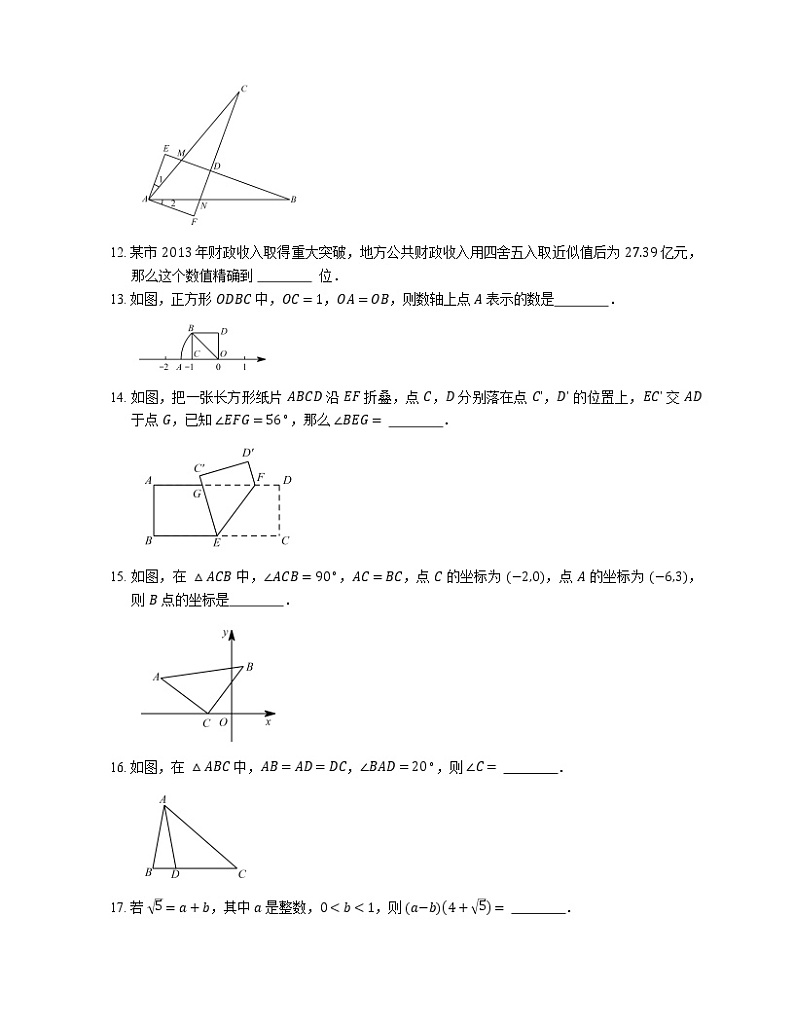
11. 如图，已知 △ABE≌△ACF，∠E=∠F=90∘，∠CMD=70∘，则 ∠2= ．

12. 某市 2013 年财政收入取得重大突破，地方公共财政收入用四舍五入取近似值后为 27.39 亿元，那么这个数值精确到 位．

13. 如图，正方形 ODBC 中，OC=1，OA=OB，则数轴上点 A 表示的数是 ．

14. 如图，把一张长方形纸片 ABCD 沿 EF 折叠，点 C，D 分别落在点 Cʹ，Dʹ 的位置上，ECʹ 交 AD 于点 G，已知 ∠EFG=56∘，那么 ∠BEG= ．

15. 如图，在 △ACB 中，∠ACB=90∘，AC=BC，点 C 的坐标为 −2,0，点 A 的坐标为 −6,3，则 B 点的坐标是 ．

16. 如图，在 △ABC 中，AB=AD=DC，∠BAD=20∘，则 ∠C= ．

17. 若 5=a+b，其中 a 是整数，0
18. 在平面直角坐标系中，将点 P−1,4 向右平移 2 个单位长度后，再向下平移 3 个单位长度，得到点 P1，则点 P1 的坐标为 ．

19. 如图，射线 OA，BA 分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中 s，t 分别表示行驶距离和时间，则这两人骑自行车的速度相差 km/h．

20. 如图，在 △ABC 中，AB=AC，D，E 是 △ABC 内的两点，AE 平分 ∠BAC，∠D=∠DBC=60∘，若 BD=5 cm，DE=3 cm，则 BC 的长是 cm．

三、解答题（共9小题；共117分）
21. 计算：−12−∣−7∣+4×2016−π0+13−1．

22. 如图，木工师傅做一个“人”字形屋梁，上弦 AB=AC=4 m，跨度 BC 为 6 m．现有一根木料打算做中柱 AD（AD 是 △ABC 的中线），请你通过计算求出中柱 AD 的长度．（只考虑长度，不计损耗）

23. 如图，正方形网格中的每个小正方形边长都是 1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．
（1）在图 1 中，画一个三角形，使它的三边长都是有理数；
（2）在图 2 中，画一个直角三角形，使它的三边长都是无理数；
（3）在图 3 中，画一个正方形，使它的面积是 10．

24. 如图，点 A，B，C，D 在同一直线上，BE∥DF，∠A=∠F，AB=FD．求证：AE=FC．

25. 如图，在三角形纸片 ABC 中，∠C=90∘，AC=6，折叠该纸片使点 C 落在 AB 边上的 D 点处，折痕 BE 与 AC 交于点 E．若 AD=BD，求折痕 BE 的长．

26. 如图，在平面直角坐标系中，已知点 A0,3，B2,4，C4,0，D2,−3，E0,−4．写出 D，C，B 关于 y 轴对称点 F，G，H 的坐标，并画出 F，G，H 点．顺次而平滑地连接 A，B，C，D，E，F，G，H，A 各点．观察你画出的图形说明它具有怎样的性质，它像我们熟知的什么图形?

27. 如图，直线 y=−43x+8 与 x 轴、 y 轴分别相交于点 A，B，设 M 是 OB 上一点，若将 △ABM 沿 AM 折叠，使点 B 恰好落在 x 轴上的点 Bʹ 处，求：
（1）点 Bʹ 的坐标；
（2）直线 AM 所对应的函数关系式．

28. 国家推行“节能减排，低碳经济”政策后，某企业推出一种叫“CNG”的改烧汽油为天然气的装置，每辆车改装费为 b 元，据市场调查知：每辆车改装前、后的燃料费（含改装费）y0，y1（单位：元）与正常运营时间 x（单位：天）之间分别满足关系式：y0=ax，y1=b+50x，如图所示．试根据图象解决下列问题：
（1）每辆车改装前每天的燃料费 a= 元；每辆车的改装费 b= 元，正常运营 天后，就可以从节省的燃料费中收回改装成本；
（2）某出租车公司一次性改装了 100 辆出租车，正常运营多少天后共节省燃料费 40 万元?

29. 某文具商店销售功能相同的 A，B 两种品牌的计算器，购买 2 个 A 品牌和 3 个 B 品牌的计算器共需 156 元；购买 3 个 A 品牌和 1 个 B 品牌的计算器共需 122 元．
（1）求这两种品牌计算器的单价；
（2）学校开学前夕，该商店对这两种计算器开展了促销活动，具体办法如下：A 品牌计算器按原价的八折销售，B 品牌计算器 5 个以上超出部分按原价的七折销售．设购买 x 个 A 品牌的计算器需要 y1 元，购买 x 个 B 品牌的计算器需要 y2 元，若购买计算器的数量超过 5 个，分别用含 x 的式子表示出 y1 和 y2；
（3）小明准备联系一部分同学集体购买同一品牌的计算器，若购买计算器的数量超过 5 个，请问购买哪种品牌的计算器更合算?说明理由．
答案
第一部分
1. A【解析】A、是轴对称图形；
B、不是轴对称图形；
C、不是轴对称图形；
D、不是轴对称图形．
2. A
3. A
4. D
5. D
6. D
7. C
8. B
9. C【解析】
如图1，S1=34a2 ，同理，S2=34c2，S3=34b2．
∵a2+b2=c2，
∴S1+S3=S2 .
∴ S3=S2−S1=45−16=29；
如图2，S5+S6=S4=11+14=25
∴S3+S4=29+25=54．
10. B
【解析】如图，延长 BG 交 CH 于点 E，
在 △ABG 和 △CDH 中，
AB=CD=10,AG=CH=8,BG=DH=6,
∴△ABG≌△CDHSSS，
AG2+BG2=AB2，
∴∠1=∠5，∠2=∠6，∠AGB=∠CHD=90∘，
∴∠1+∠2=90∘，∠5+∠6=90∘，
又 ∵∠2+∠3=90∘，∠4+∠5=90∘，
∴∠1=∠3=∠5，∠2=∠4=∠6，
在 △ABG 和 △BCE 中，
∠1=∠3,AB=BC,∠2=∠4,
∴△ABG≌△BCEASA，
∴BE=AG=8，CE=BG=6，∠BEC=∠AGB=90∘，
∴GE=BE−BG=8−6=2，
同理可得 HE=2，
在 Rt△GHE 中，GH=GE2+HE2=22+22=22．
第二部分
11. 20∘
12. 百万
13. −2
14. 68∘
15. 1,4
16. 40∘
【解析】∵AB=AD，∠BAD=20∘，
∴∠B=12180∘−∠BAD=12180∘−20∘=80∘．
∵∠ADC 是 △ABD 的外角，
∴∠ADC=∠B+∠BAD=80∘+20∘=100∘．
∵AD=DC．
∴∠C=12180∘−∠ADC=12180∘−100∘=40∘．
17. 11
18. 1,1
19. 4
20. 8
第三部分
21. −12−∣−7∣+4×2016−π0+13−1=1−7+2×1+3=1−7+2+3=−1.
22. ∵ AB=AC=4 m，AD 是 △ABC 的中线，BC=6 m，
∴ AD⊥BC，BD=12BC=3 m，
在 Rt△ABD 中，由勾股定理，得 AD=AB2−BD2=42−32=7m，
即这根中柱 AD 的长度是 7 m．
23. （1） 如图 1：（答案不唯一）
（2） 如图 2：（答案不唯一）
（3） 如图 3：（答案不唯一）
24. ∵ BE∥DF，
∴ ∠ABE=∠D，
在 △ABE 和 △FDC 中，
∠ABE=∠D,AB=FD,∠A=∠F,
∴ △ABE≌△FDC，
∴ AE=FC．
25. ∵ 折叠 △ABC 纸片使点 C 落在 AB 边上的 D 点处，
∴ BC=BD，∠CBE=∠ABE，
∵ BD=AD，
∴ BC=12AB，
∴ sinA=0.5，
∴ ∠A=30∘，
∴ BC=33AC=33×6=23，
∵ ∠ABC=90∘−∠A=60∘，
∴ ∠CBE=12∠ABC=30∘，
在 Rt△BCE 中，
∵ ∠CBE=30∘，
∴ CE=33BC=2，
∴ BE=2CE=4．
26. 由题意得，F−2,−3，G−4,0，H−2,4，
这个图形关于 y 轴对称，是我们熟知的轴对称图形．
27. （1） y=−43x+8，
令 x=0，则 y=8，
令 y=0，则 x=6，
∴A6,0，B0,8，
∴OA=6，OB=8，
∴AB=10，
∵ABʹ=AB=10，
∴OBʹ=10−6=4，
∴ 点 Bʹ 的坐标为：−4,0．
（2） 设 OM=m，则 BʹM=BM=8−m，
在 Rt△OMBʹ 中，m2+42=8−m2，
解得：m=3，
∴M 的坐标为：0,3，
设直线 AM 的解析式为 y=kx+b，
则 6k+b=0,b=3,
解得：k=−12,b=3,
故直线 AM 的解析式为：y=−12x+3．
28. （1） 90；4000；100
（2） 设正常运营 x 天后节省材料费 40 万元，
依据题意及图象得：改装前、后的燃料费每天分别为 90 元，50 元，
则：
100×90−50x=400000+100×4000,
解得：
x=200,
答：200 天后共节省燃料费 40 万元．
29. （1） 设 A 品牌的计算器的价格为 m 元，B 品牌的计算器的价格为 n 元，
根据题意得
2m+3n=156,3m+n=122,
解得
m=30,n=32.
答：A 品牌的计算器的价格为 30 元，B 品牌的计算器的价格为 32 元．
（2） 根据题意得 y1=0.8⋅30x=24x，
当 x>5，y2=32×5+0.7×32x−5=22.4x+48．
（3） 当购买计算器的数量超过 5 个，
当 y1当 y1=y2 时，24x=22.4x+48，解得 x=30；
当 y1>y2 时，24x>22.4x+48，解得 x>30；
所以购买计算器的数量超过 5 个而不足 30 个时，购买 A 品牌的计算器更合算；
购买计算器的数量为 30 个时，购买 A 品牌和 B 品牌的计算器一样合算；
购买计算器的数量超过 30 个时，购买 B 品牌的计算器更合算．