2018年江苏省无锡市滨湖区中考二模数学试卷

这是一份2018年江苏省无锡市滨湖区中考二模数学试卷，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. −5 的倒数是
A. −15B. 15C. −5D. 5

2. 式子 3−x 在实数范围内有意义，则 x 的取值范围是
A. x>3B. x≥3C. x<3D. x≤3

3. 下列运算正确的是
A. −2x23=−6x6B. y+x−y+x=y2−x2
C. 2x+2y=4xyD. x4÷x2=x2

4. 已知一次函数 y=kx+1k≠0 的图象经过点 A，且函数值 y 随 x 的增大而减小，则点 A 的坐标可能是
A. 2,4B. −1,2C. −1,−4D. 5,1

5. 反比例函数 y=1−2kx 的图象经过点 −2,3，则 k 的值为
A. 72B. −72C. 6D. −6

6. 某中学足球队的 18 名队员的年龄情况如下表：则这些队员年龄的众数和中位数分别是
年龄单位:岁1415161718人数36441
A. 15，15B. 15，15.5C. 15，16D. 16，15

7. 下列命题正确的是
A. 一组对边平行，另一组对边相等的四边形是平行四边形
B. 对角线相等的四边形是矩形
C. 一组邻边相等的矩形是正方形
D. 对角线互相垂直的四边形是菱形

8. 已知点 Am2−2,5m+4 在第一象限角平分线上，则 m 的值为
A. 6B. −1C. 2 或 3D. −1 或 6

9. 如图，已知等腰 △ABC，AB=BC，D 是 AC 上一点，线段 BE 与 BA 关于直线 BD 对称，射线 CE 交射线 BD 于点 F，连接 AE，AF．则下列关系正确的是
A. ∠AFE+∠ABE=180∘B. ∠AEF=12∠ABC
C. ∠AEC+∠ABC=180∘D. ∠AEB=∠ACB

10. 如图，在平面直角坐标系中，A0,3，B3,0，以点 B 为圆心、 2 为半径的 ⊙B 上有一动点 P．连接 AP，若点 C 为 AP 的中点，连接 OC，则 OC 的最小值为
A. 1B. 22−1C. 2D. 322−1

二、填空题（共8小题；共40分）
11. 9 的平方根是 ．

12. 根据滨湖区旅游局数据统计显示，今年“五一”小长假，鼋头渚、灵山圣境、三国水浒城三大 5A 景区共接待旅游总人数 254000 人，这个数据用科学记数法可表示为 人．

13. 分解因式：2x2−12x+18= ．

14. 用一个圆心角为 120∘，半径为 6 的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是 ．

15. 小丽计算数据方差时，使用公式 s2=155−x2+8−x2+13−x2+14−x2+15−x2，则公式中 x= ．

16. 如图，BD 为 ⊙O 的直径，点 A 为 BDC 的中点，∠ABD=35∘，则 ∠DBC= ∘．

17. 如图，在 △ABC 中，AC=4，将 △ABC 绕点 C 按逆时针旋转 30∘ 得到 △FGC，则图中阴影部分的面积为 ．

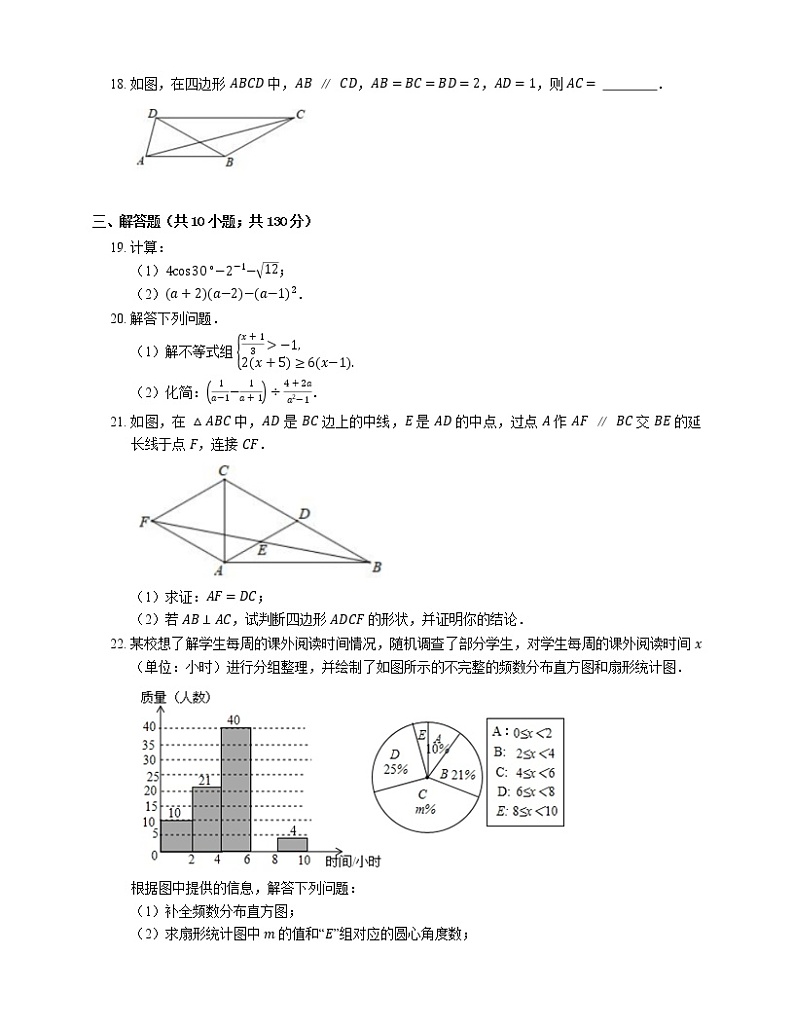
18. 如图，在四边形 ABCD 中，AB∥CD，AB=BC=BD=2，AD=1，则 AC= ．

三、解答题（共10小题；共130分）
19. 计算：
（1）4cs30∘−2−1−12；
（2）a+2a−2−a−12．

20. 解答下列问题．
（1）解不等式组 x+13>−1,2x+5≥6x−1.
（2）化简：1a−1−1a+1÷4+2aa2−1．

21. 如图，在 △ABC 中，AD 是 BC 边上的中线，E 是 AD 的中点，过点 A 作 AF∥BC 交 BE 的延长线于点 F，连接 CF．
（1）求证：AF=DC；
（2）若 AB⊥AC，试判断四边形 ADCF 的形状，并证明你的结论．

22. 某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间 x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分布直方图和扇形统计图．
根据图中提供的信息，解答下列问题：
（1）补全频数分布直方图；
（2）求扇形统计图中 m 的值和“E”组对应的圆心角度数；
（3）请估计该校 3000 名学生中每周的课外阅读时间不小于 6 小时的人数．

23. 甲，乙，丙三位学生进入了“校园朗诵比赛”冠军、亚军和季军的决赛，他们将通过抽签来决定比赛的出场顺序．
（1）求甲第一个出场的概率；
（2）求甲比乙先出场的概率．

24. 如图，已知矩形 ABCD，E 是 AB 上一点．
（1）利用尺规分别在 BC，CD，AD 上确定点 F，G，H，使得四边形 EFGH 是特殊的平行四边形；（提示：①保留作图痕迹，不写作法；②只需作出一种情况即可．）
（2）在（1）的条件下，若 AB=7，AD=8，AE=4，则所作四边形的周长为 ．

25. 随着“一带一路”的不断建设与深化，我国不少知名企业都积极拓展海外市场，参与投资经营．某著名手机公司在某国经销某种型号的手机，受该国政府经济政策与国民购买力双重影响，手机价格不断下降．分公司在该国某城市的一家手机销售门店，今年 5 月份的手机售价比去年同期每台降价 1000 元，若卖出同样多的手机，去年销售额可达 10 万元，今年销售额只有 8 万元．
（1）今年 5 月份每台手机售价多少元?
（2）为增加收入，分公司决定拓展产品线，增加经销某种新型笔记本电脑．已知手机每台成本为 3500 元，笔记本电脑每台成本为 3000 元，分公司预计用不少于 4.8 万元的成本资金少量试生产这两种产品共 15 台，但因资金所限不能超过 5 万元，共有几种生产方案?
（3）如果笔记本电脑每台售价 3800 元，现为打开笔记本电脑的销路，公司决定每售出 1 台笔记本电脑，就返还顾客现金 a 元，要使（2）中各方案获利相同，a 的值应为多少?

26. 如图，△ABC 是以 BC 为底边的等腰三角形，点 A，C 分别是一次函数 y=−34x+3 的图象与 y 轴、 x 轴的交点，点 B 在二次函数 y=18x2+bx+c 的图象上，且该二次函数图象上存在一点 D 使四边形 ABCD 能构成平行四边形．
（1）求该二次函数的解析式；
（2）动点 P 从 A 到 D 运动，同时动点 Q 从 C 到 A 运动，两点都以每秒 1 个单位的速度运动，问：
①当 △APQ 是直角三角形时，求点 P 的坐标；
②四边形 PDCQ 的面积是否有最小值?若有，求出面积的最小值和点 P 的坐标；若没有，请说明理由．

27. 在 △ABC 中，∠ABC=45∘，BC=4，tanC=3，AH⊥BC 于点 H，点 D 在 AH 上，且 DH=CH，连接 BD．
（1）如图 1，将 △BHD 绕点 H 旋转，得到 △EHF（点 B，D 分别与点 E，F 对应），连接 AE，点 F 落在 AC 上时（F 不与 C 重合），求 AE 的长．
（2）如图 2，△EHF 是由 △BHD 绕点 H 逆时针旋转 30∘ 得到的，射线 CF 与 AE 相交于点 G，连接 GH，试探究线段 GH 与 EF 之间满足的等量关系，并说明理由．

28. 如图，在平行四边形 ABCD 中，AB=4，AD=2，∠A=60∘．动点 P 从点 A 出发，沿 AB 以每秒 1 个单位长度的速度向终点 B 运动，过点 P 作 PQ⊥AB 交折线 AD−DC 于点 Q，以 PQ 为边在 PQ 右侧作等边三角形 PQN．将 △PQN 绕 QN 的中点旋转 180∘ 得到 △MNQ．设四边形 PQMN 与平行四边形 ABCD 重叠部分图形的面积为 S（平方单位），点 P 的运动时间为 ts0≤t≤4．
（1）当点 N 在边 BC 上时，t 的值是 ，当 MN 经过点 C 时，t 的值是 ；
（2）当点 Q 在 CD 边上，且四边形 PQMN 与平行四边形 ABCD 重叠部分图形是四边形时，求 S 与 t 之间的函数关系式；
（3）设平行四边形 ABCD 和四边形 PQMN 的对角线的交点分别是点 O，Oʹ．当 OOʹ 最短时，直接写出 t 的值．
答案
第一部分
1. A【解析】∵−5×−15=1，
∴−5 的倒数是 −15．
2. D【解析】依题意，得 3−x≥0，
解得，x≤3．
3. D【解析】A、 −2x23=−8x6，故本项错误；
B、 y+x−y+x=x2−y2，故本项错误；
C、 2x 与 2y 不能合并，故本项错误；
D、 x4÷x2=x2，故本项正确，
故选：D．
4. B【解析】∵ 一次函数 y=kx+1k≠0 的函数值 y 随 x 的增大而减小，
∴k<0．
A．∵ 当 x=2，y=4 时，2k+1=4，解得 k=1.5>0，
∴ 此点不符合题意，故本选项错误；
B．∵ 当 x=−1，y=2 时，−k+1=2，解得 k=−1<0，
∴ 此点符合题意，故本选项正确；
C．∵ 当 x=−1，y=−4 时，−k+1=−4，解得 k=5>0，
∴ 此点不符合题意，故本选项错误；
D．∵ 当 x=5，y=1 时，5k+1=1，解得 k=0，
∴ 此点不符合题意，故本选项错误．
5. A
【解析】∵ 反比例函数 y=1−2kx 的图象经过点 −2,3，
∴3=1−2k−2，
解得，k=72，
故选：A．
6. B【解析】根据图表数据，同一年龄人数最多的是 15 岁，共 6 人，所以众数是 15；
18 名队员中，按照年龄从大到小排列，第 9 名队员的年龄是 15 岁，第 10 名队员的年龄是 16 岁，
所以，中位数是 15+162=15.5．
7. C【解析】A、例如等腰梯形，故本选项错误；
B、对角线相等且互相平分的平行四边形是矩形，故本选项错误；
C、一组邻边相等的矩形是正方形，故本选项正确；
D、根据菱形的判定，应是对角线互相垂直的平行四边形，故本选项错误．
故选：C．
8. A【解析】∵ 点 Am2−2,5m+4 在第一象限角平分线上，
∴m2−2=5m+4，
∴m2−5m−6=0，
解得 m1=−1，m2=6，
当 m=−1 时，m2−2=−1，
点 A−1,−1 在第三象限，不符合题意，
∴m 的值为 6．
9. B【解析】由轴对称的性质可得，四边形 ABEF 中，AB=EB，AF=EF，
∴∠BAF=∠BEF，
∵ 等腰 △BCE 中，∠BEC<90∘，
∴∠BEF>90∘，
∴∠BAF>90∘，
∴ 四边形 ABEF 中，∠AFE+∠ABE<180∘，故A错误；
∵△ABE 中，∠AEB=180∘−∠ABE2，
△BCE 中，∠BEC=180∘−∠CBE2，
∴∠AEF=180∘−∠AEB−∠BEC=180∘−180∘−∠ABE2−180∘−∠CBE2=12∠ABE+∠CBE=12∠ABC,
故B正确；
∵AB=CB=EB，
∴∠AEB=∠EAB，∠BEC=∠BCE，
∴∠AEC=∠EAB+∠ECB>∠CAB+∠ACB，
∴∠AEC+∠ABC>∠CAB+∠ACB+∠ABC=180∘，故C错；
∵∠AEB=∠EAB，∠BAC=∠BCA，∠BAE>BAC，
∴∠AEB>ACB，故D错；
故选：B．
10. D
【解析】当点 P 运动到 AB 的延长线上时，即如图中点 P1，C1 是 AP1 的中点，
当点 P 在线段 AB 上时，C2 是中点，取 C1C2 的中点为 D，
点 C 的运动路径是以 D 为圆心，以 DC1 为半径的圆（CA:PA=1:2，则点 C 轨迹和点 P 轨迹相似，所以点 C 的轨迹就是圆），当 O，C，D 共线时，OC 的长最小，
设线段 AB 交 ⊙B 于 Q，
Rt△AOB 中，OA=3，OB=3，
∴AB=32，
∵⊙B 的半径为 2，
∴BP1=2，AP1=32+2，
∵C1 是 AP1 的中点，
∴AC1=322+1，AQ=32−2，
∵C2 是 AQ 的中点，
∴AC2=C2Q=322−1，
C1C2=232+1−322−1=2，即 ⊙D 的半径为 1，
∵AD=322−1+1=322=12AB，
∴OD=12AB=322．
∴OC=322−1
方法二：如图，取 Aʹ0,−3，连接 PAʹ．
根据三角形中位线定理可知：PAʹ=2OC，求出 PAʹ 的最小值即可解决问题．
第二部分
11. ±3
【解析】∵±3 的平方是 9，
∴9 的平方根是 ±3．
12. 2.54×105
【解析】254000 人，这个数据用科学记数法可表示为 2.54×105 人．
13. 2x−32
【解析】2x2−12x+18=2x2−6x+9=2x−32．
故答案为：2x−32．
14. 2
【解析】扇形的弧长 =120π×6180=4π，
∴ 圆锥的底面半径为 4π÷2π=2．
故答案为：2．
15. 11
【解析】∵s2=155−x2+8−x2+13−x2+14−x2+15−x2，
∴x=5+8+13+14+155=11．
16. 20
【解析】连接 AD．
∵BD 是直径，
∴∠BAD=90∘，
∵∠ABD=35∘，
∴∠ADB=55∘，
∴∠ACB=∠ADB=55∘，
∵A 为弧 BDC 的中点，
∴AB=AC，
∴∠ABC=∠ACB=55∘，
∵∠ABD=35∘，
∴∠DBC=55∘−35∘=20∘．
17. 43π
【解析】由题意得，△CAB 的面积 =△CFG 的面积，
由图形可知，阴影部分的面积 =△CFG 的面积 + 扇形 CAF 的面积 −△CBA 的面积，
∴ 阴影部分的面积 = 扇形 CAF 的面积 =30π×42360=43π．
18. 15
【解析】过点 D 作 DE⊥AB 于点 E，过点 C 作 CF⊥AB 交 AB 延长线于点 F，
∴∠AED=∠BED=∠F=90∘，
设 AE=x，
∵AB=BC=BD=2，AD=1，
∴BE=AB−AE=2−x
∵ 在 Rt△ADE 中，AE2+DE2=AD2，
在 Rt△BDE 中，BE2+DE2=BD2，
∴DE2=AD2−AE2=BD2−BE2，
得：12−x2=22−2−x2，
解得：x=14，
∴DE2=AD2−AE2=12−142=1516，
∵AB∥CD，
∴CF=DE，
∴ 在 Rt△BCF 中，BF=BC2−CF2=22−1516=74，
∴AF=AB+BF=2+74=154，
∴ 在 Rt△ACF 中，AC=AF2+CF2=1542+1516=15．
第三部分
19. （1） 原式=4×32−12−23=−12.
（2） 原式=a2−4−a2−2a+1=a2−4−a2+2a−1=2a−5.
20. （1） 解不等式 x+13>−1，得：
x>−4.
解不等式 2x+5≥6x−1，得：
x≤4.
则不等式组的解集为
−4 （2） 原式=a+1a+1a−1−a−1a+1a−1÷2a+2a+1a−1=2a+1a−1⋅a+1a−12a+2=1a+2.
21. （1） ∵AF∥CD，E 是 AD 的中点，
∴∠AFE=∠DBE，EF=EB，
又 ∠AEF=∠DEB，
∴△AEF≌△DEBASA，
∴AF=DB，
∵AD 是 BC 边上的中线，
∴DB=DC，
∴AF=DC．
（2） 四边形 ADCF 是菱形．
证明：
∵ 由（1）知 AF=CD，
又 AF∥CD，
∴ 四边形 ADCF 是平行四边形，
∵AB⊥AC，
∴△ABC 是直角三角形，
∵AD 是 BC 边上的中线，
∴AD=DC=DB，
∵AF=CD，
∴AF=AD，
∴ 四边形 ADCF 是菱形．
22. （1） 数据总数为：21÷21%=100，
第四组频数为：100−10−21−40−4=25，
频数分布直方图补充如下：
（2） m=40÷100×100=40；
“E”组对应的圆心角度数为：360∘×4100=14.4∘；
（3） 3000×25%+4100=870（人）．
即估计该校 3000 名学生中每周的课外阅读时间不小于 6 小时的人数是 870 人．
23. （1） 画树状图如下：
所有等可能的情况有 6 种，其中甲第一个出场的情况有 2 种，
则 P（甲第一个出场）=26=13．
（2） 甲比乙先出场的情况有 3 种，
则 P（甲比乙先出场）=36=12．
24. （1） 下列三种图形中的一种；
（2） 73454 或 613 或 105
【解析】若是图 1，周长为 73454；若是图 2，周长为 613；若是图 3，周长为 105．
25. （1） 设今年 5 月份手机每台售价为 m 元，则去年同期每台售价为 m+1000 元．
根据题意得：
100000m+1000=80000m.
解得：
m=4000.
经检验，m=4000 是原方程的根且符合题意．
答：今年 5 月份手机每台售价为 4000 元．
（2） 设生产手机 x 台，则生产笔记本电脑 15−x 台，
根据题意得：
3500x+300015−x≥48000,3500x+300015−x≤50000.
解得：
6≤x≤10.∴x
的正整数解为 6，7，8，9，10．
答：共有 5 种生产方案．
（3） 设总获利为 w 元，
根据题意得：w=4000−3500x+3800−3000−a15−x=a−300x+12000−15a．
∵w 的值与 x 值无关，
∴a−300=0，即 a=300．
答：当 a=300 时，（2）中所有方案获利相同．
26. （1） 由 y=−34x+3，得 A0,3，C4,0．
由于 B，C 关于 OA 对称，
∴B−4,0，BC=8．
∵AD∥BC，AD=BC，
∴D8,3．
将 B−4,0，D8,3 分别代入 y=18x2+bx+c，
得 2−4b+c=0,8+8b+c=3, 解得：b=−14,c=−3.
∴ 该二次函数的解析式为：y=18x2−14x−3．
（2） ①设点 P，Q 运动的时间为 t．
如图 1，在 △APQ 中，AP=t，AQ=AC−CQ=5−t，cs∠PAQ=cs∠ACO=45．
当 PQ⊥AC 时，AQAP=45．∴5−tt=45．
解得：t=259；
如图 2，当 QP⊥AD 时，这时 APAQ=45，
∴t5−t=45，解得：t=209．
即 AP=259 或 AP=209 时，△APQ 是直角三角形．
②如图 3，过点 Q 作 QH⊥AD，垂足为 H．
由于 S△APQ=12AP⋅QH=12AP⋅AQsin∠PAQ=12t5−t×35=−310t2+32t，
S△ACD=12AD⋅OA=12×8×3=12，
∴S四边形PDCQ=S△ACD−S△APQ=12−−310t2+32t=310t−522+818．
∴ 当 t=52，即 AP=52 时，四边形 PDCQ 的最小值是 818．
27. （1） 如图 3，
在 Rt△AHC 中，
∵tanC=3，
∴AHCH=3，
设 CH=x，
∴BH=AH=3x，
∵BC=4，
∴3x+x=4，
∴x=1，
∴AH=3，CH=1，
由旋转知，∠EHF=∠BHD=∠AHC=90∘，EH=AH=3，CH=DH=FH，
∴∠EHF+∠AHF=∠AHC+∠AHF，
∴∠EHA=∠FHC，EHAH=FHHC=1，
∴△EHA∽△FHC，
∴∠EAH=∠C，
∴tan∠EAH=tanC=3，
过点 H 作 HP⊥AE，
∴HP=3AP，AE=2AP，
在 Rt△AHP 中，AP2+HP2=AH2，
∴AP2+3AP2=9，
∴AP=31010，
∴AE=3105．
（2） 如图 4，
∵△EHF 是由 △BHD 绕点 H 逆时针旋转 30∘ 得到，
∴HD=HF，∠AHF=30∘，
∴∠CHF=90∘+30∘=120∘，
由（1）有，△AEH 和 △FHC 都为等腰三角形，
∴∠GAH=∠HCG=30∘，
∴CG⊥AE，
∴ 点 C，H，G，A 四点共圆，
∴∠CGH=∠CAH，
设 CG 与 AH 交于点 Q，
∵∠AQC=∠GQH，
∴△AQC∽△GQH，
∴ACHG=AQGQ=1sin30∘=2，
∵△EHF 是由 △BHD 绕点 H 逆时针旋转 30∘ 得到，
∴EF=BD，
由（1）知，BD=AC，
∴EF=AC，
∴EFHG=1sin30∘=2，
即：EF=2HG．
28. （1） 3；72
【解析】如图 1 中，当点 N 在边 BC 上时，
由题意：PB=BN=CN=1，
∴PA=AB−PB=3，
∴t=3 s 时，点 N 在直线 BC 上．
如图 2 中，当 MN 经过点 C 时，
由题意：PA−DQ=1，
∴t−4−32=1，
∴t=72 s．
（2） 如图 3 中，当 1≤t≤3 时，重叠部分是四边形 GQPN．
S=12×3+32⋅32=938．
如图 4 中，当 3.5≤t≤4 时，重叠部分是四边形 CQPG．
S=S梯形CQPB−S△PBG=324−t+5−t−344−t2=−34t2+3t+32.
（3） 74．
【解析】如图 5 中，由题意可知点 Oʹ 在直线 HG 上运动，DH=CG=14AD=12．
当 OOʹ⊥CD 于 E 时，OOʹ 的值最小，
此时 QE=34，DE=32，
∴DQ=32−34=34，
∴PA=1+34=74s．