

专题04 因动点产生的相似、全等问题-版突破中考数学压轴之学霸秘笈大揭秘(教师版)
展开
【类型综述】
函数中因动点产生的相似三角形问题一般有三个解题途径
① 求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
【方法揭秘】
相似三角形的判定定理有3个,其中判定定理1和判定定理2都有对应角相等的条件,因此探求两个三角形相似的动态问题,一般情况下首先寻找一组对应角相等.
判定定理2是最常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验.
如果已知∠A=∠D,探求△ABC与△DEF相似,只要把夹∠A和∠D的两边表示出来,按照对应边成比例,分和两种情况列方程.
应用判定定理1解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等.
应用判定定理3解题不多见,根据三边对应成比例列连比式解方程(组).
还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题.
求线段的长,要用到两点间的距离公式,而这个公式容易记错.理解记忆比较好.
如图1,如果已知A、B两点的坐标,怎样求A、B两点间的距离呢?
我们以AB为斜边构造直角三角形,直角边与坐标轴平行,这样用勾股定理就可以求斜边AB的长了.水平距离BC的长就是A、B两点间的水平距离,等于A、B两点的横坐标相减;竖直距离AC就是A、B两点间的竖直距离,等于A、B两点的纵坐标相减.
图1
【典例分析】
例1 如图1,已知直线y=-x+3与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,点P在线段OA上,从点O出发,向点A以每秒1个单位的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以每秒个单位的速度匀速运动,连结PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)问:当t为何值时,△APQ为直角三角形;
(3)过点P作PE//y轴,交AB于点E,过点Q作QF//y轴,交抛物
线于点F,连结EF,当EF//PQ时,求点F的坐标;
(4)设抛物线顶点为M,连结BP、BM、MQ,问:是否存在t的值,使以B、Q、M为顶点的三角形与以O、B、P为顶点的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
思路点拨
1.在△APQ中,∠A=45°,夹∠A的两条边AP、AQ都可以用t表示,分两种情况讨论直角三角形APQ.
2.先用含t的式子表示点P、Q的坐标,进而表示点E、F的坐标,根据PE=QF列方程就好了.
3.△MBQ与△BOP都是直角三角形,根据直角边对应成比例分两种情况讨论.
满分解答
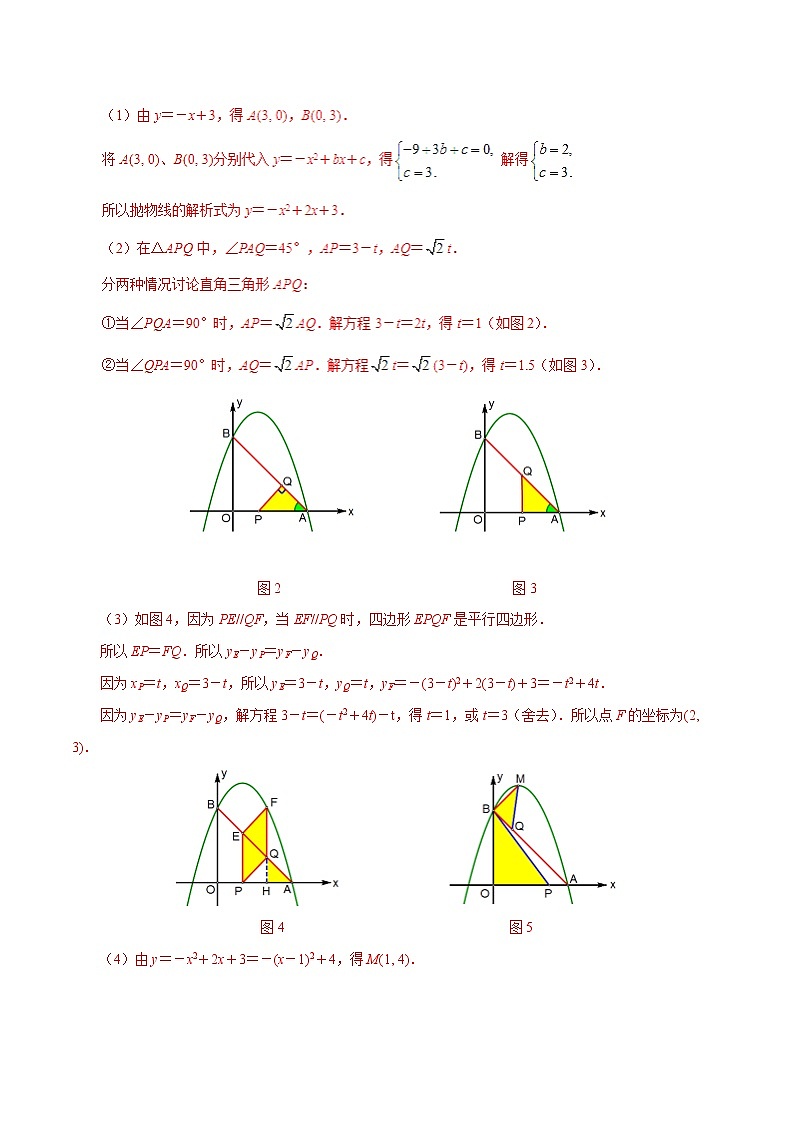
图2 图3
(3)如图4,因为PE//QF,当EF//PQ时,四边形EPQF是平行四边形.
所以EP=FQ.所以yE-yP=yF-yQ.
因为xP=t,xQ=3-t,所以yE=3-t,yQ=t,yF=-(3-t)2+2(3-t)+3=-t2+4t.
因为yE-yP=yF-yQ,解方程3-t=(-t2+4t)-t,得t=1,或t=3(舍去).所以点F的坐标为(2, 3).
图4 图5
(4)由y=-x2+2x+3=-(x-1)2+4,得M(1, 4).
考点伸展
第(3)题也可以用坐标平移的方法:由P(t, 0),E(t, 3-t),Q(3-t, t),按照P→E方向,将点Q向上平移,得F(3-t, 3).再将F(3-t, 3)代入y=-x2+2x+3,得t=1,或t=3.
例2 二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3, 0)、B(1, 0)两点,与y轴交于点C(0,-3m)(m>0),顶点为D.
(1)求该二次函数的解析式(系数用含m的代数式表示);
(2)如图1,当m=2时,点P为第三象限内抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值;
(3)如图2,当m取何值时,以A、D、C三点为顶点的三角形与△OBC相似?
图1 图2
思路点拨
1.用交点式求抛物线的解析式比较简便.
2.连结OP,△APC可以割补为:△AOP与△COP的和,再减去△AOC.
3.讨论△ACD与△OBC相似,先确定△ACD是直角三角形,再验证两个直角三角形是否相似.
4.直角三角形ACD存在两种情况.
满分解答
图3 图4 图5
(3)如图4,过点D作y轴的垂线,垂足为E.过点A作x轴的垂线交DE于F.
由y=m(x+3)(x-1)=m(x+1)2-4m,得D(-1,-4m).
在Rt△OBC中,OB∶OC=1∶3m.
如果△ADC与△OBC相似,那么△ADC是直角三角形,而且两条直角边的比为1∶3m.
①如图4,当∠ACD=90°时,.所以.解得m=1.
此时,.所以.所以△CDA∽△OBC.
考点伸展
第(2)题还可以这样割补:如图6,过点P作x轴的垂线与AC交于点H.
由直线AC:y=-2x-6,可得H(x,-2x-6).
又因为P(x, 2x2+4x-6),所以HP=-2x2-6x.
因为△PAH与△PCH有公共底边HP,高的和为A、C两点间的水平距离3,所以
S=S△APC=S△APH+S△CPH
=(-2x2-6x)=.
例3如图1,在平面直角坐标系中,双曲线(k≠0)与直线y=x+2都经过点A(2, m).
(1)求k与m的值;
(2)此双曲线又经过点B(n, 2),过点B的直线BC与直线y=x+2平行交y轴于点C,联结AB、AC,求△ABC的面积;
(3)在(2)的条件下,设直线y=x+2与y轴交于点D,在射线CB上有一点E,如果以点A、C、E所组成的三角形与△ACD相似,且相似比不为1,求点E的坐标.
图1
思路点拨
1.直线AD//BC,与坐标轴的夹角为45°.
2.求△ABC的面积,一般用割补法.
3.讨论△ACE与△ACD相似,先寻找一组等角,再根据对应边成比例分两种情况列方程.
满分解答
(3)由A(2, 4) 、D(0, 2) 、C (0,-2),得AD=,AC=.
由于∠DAC+∠ACD=45°,∠ACE+∠ACD=45°,所以∠DAC=∠ACE.
所以△ACE与△ACD相似,分两种情况:
①如图3,当时,CE=AD=.
此时△ACD≌△CAE,相似比为1.
图3 图4
考点伸展
第(2)题我们在计算△ABC的面积时,恰好△ABC是直角三角形.
一般情况下,在坐标平面内计算图形的面积,用割补法.
如图5,作△ABC的外接矩形HCNM,MN//y轴.
由S矩形HCNM=24,S△AHC=6,S△AMB=2,S△BCN=8,得S△ABC=8.
例4 如图1,Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)如图2,连接AQ、CP,若AQ⊥CP,求t的值;
(3)试证明:PQ的中点在△ABC的一条中位线上.
图1 图2
思路点拨
1.△BPQ与△ABC有公共角,按照夹角相等,对应边成比例,分两种情况列方程.[来源:]
2.作PD⊥BC于D,动点P、Q的速度,暗含了BD=CQ.
3.PQ的中点H在哪条中位线上?画两个不同时刻P、Q、H的位置,一目了然.
满分解答
图3 图4
(2)作PD⊥BC,垂足为D.
在Rt△BPD中,BP=5t,cosB=,所以BD=BPcosB=4t,PD=3t.
当AQ⊥CP时,△ACQ∽△CDP.
所以,即.解得.
图5 图6
考点伸展
本题情景下,如果以PQ为直径的⊙H与△ABC的边相切,求t的值.
如图7,当⊙H与AB相切时,QP⊥AB,就是,.
如图8,当⊙H与BC相切时,PQ⊥BC,就是,t=1.
如图9,当⊙H与AC相切时,直径,
半径等于FC=4.所以.
解得,或t=0(如图10,但是与已知0<t<2矛盾).
图7 图 8 图9 图10
例5如图1,已知抛物线(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B是左侧),与y轴的正半轴交于点C.
(1)点B的坐标为______,点C的坐标为__________(用含b的代数式表示);
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
图1
思路点拨
1.第(2)题中,等腰直角三角形PBC暗示了点P到两坐标轴的距离相等.
2.联结OP,把四边形PCOB重新分割为两个等高的三角形,底边可以用含b的式子表示.
3.第(3)题要探究三个三角形两两相似,第一直觉这三个三角形是直角三角形,点Q最大的可能在经过点A与x轴垂直的直线上.
满分解答
图2 图3
图4 图5
考点伸展
第(3)题的思路是,A、C、O三点是确定的,B是x轴正半轴上待定的点,而∠QOA与∠QOC是互余的,那么我们自然想到三个三角形都是直角三角形的情况.
这样,先根据△QOA与△QOC相似把点Q的位置确定下来,再根据两直角边对应成比例确定点B的位置.
如图中,圆与直线x=1的另一个交点会不会是符合题意的点Q呢?
如果符合题意的话,那么点B的位置距离点A很近,这与OB=4OC矛盾.
例6如图1,已知抛物线的方程C1: (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线C1过点M(2, 2),求实数m的值;
(2)在(1)的条件下,求△BCE的面积;
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;
(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
图1
思路点拨
1.第(3)题是典型的“牛喝水”问题,当H落在线段EC上时,BH+EH最小.
2.第(4)题的解题策略是:先分两种情况画直线BF,作∠CBF=∠EBC=45°,或者作BF//EC.再用含m的式子表示点F的坐标.然后根据夹角相等,两边对应成比例列关于m的方程.
满分解答
(4)①如图3,过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.
由于∠BCE=∠FBC,所以当,即时,△BCE∽△FBC.
设点F的坐标为,由,得.
解得x=m+2.所以F′(m+2, 0).
由,得.所以.
由,得.
整理,得0=16.此方程无解.
图2 图3 图4[来源:Z#xx#k.Com]
考点伸展
第(4)题也可以这样求BF的长:在求得点F′、F的坐标后,根据两点间的距离公式求BF的长.
【变式训练】
1.如图,在四边形中,,,,,,点为边上一动点,若与是相似三角形,则满足条件的点的个数是( )
A.个 B.个 C.个 D.个
【答案】C
【解析】分类讨论
①
设,则,,,,
②,设为,则,,,,,综上,为,,,则满足题意,有三个点.
2.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2㎝,BC=6㎝,AB=7㎝,点P是从点B出发在射线BA上的一个动点,运动的速度是1㎝/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
A.5个 B.4个 C.3个 D.2个
【答案】A
【解析】
考点:相似三角形的判定与性质.
3.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.
A.1 B.1或3 C.1或7 D.3或7
【答案】C
【解析】
4.如图,在中,,点是边上一动点(不与、重合),,交于点,且,则线段的最大值为________.
【答案】
【解析】
过点A作AG⊥BC于G,
设BD=x,则CD=16-x,
∵∠ADC=∠B+∠BAD,即∠ADE+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
∵∠C=∠B,
∴△ABD∽△DCE,
∴,即,
∴CE=,
∴当x=8时,EC有最大值,最大值为6.4.
故答案为:6.4.
5.如图, 中, , 分别是上动点,且,当=_______时,才能使和全等.
【答案】3或8
【解析】试题解析:分为两种情况:①当AP=3时,
∵BC=3,
∴AP=BC,
∵∠C=90°,AE⊥AC,
∴∠C=∠QAP=90°,
∴在Rt△ABC和Rt△QAP中,
∴Rt△ABC≌Rt△QAP(HL),
6.如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 .下列结论: ①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或; ④CD2=CE•CA. 其中正确的结论是________ (把你认为正确结论的序号都填上)
【答案】①②③
【解析】
7.如图,在中,,,,点是边上的动点(点与点、不重合),过动点作交于点.若与相似,则________.
【答案】或
【解析】
∵∠BAC=90°,PD∥AB,
∴∠PDA=90°,
又∵∠C=60°,
∴∠APD=30°或60°时,△ABC与△DAP相似,
∴∠APD=30°或60°.
8.如图,直线与轴交于点,与轴交于点,抛物线,经过点.
(1)求抛物线的解析式
(2)已知点是抛物线上的一个动点,并且点在第二象限内,过动点作轴于点,交线段于点.
①如图1,过作轴于点,交抛物线于两点(点位于点的左侧),连接,当线段的长度最短时,求点的坐标,
②如图2,连接,若以为顶点的三角形与相似,求的面积.
【答案】(1) ;(2) ①点的坐标为,点的坐标为,点的坐标为;②
【解析】
(2) ①由题意可知,四边形是矩形,所以.
由(1)可知,
当时,最短,即最短,
此时点是的中点,
点的坐标为,点的坐标为
②当时(如图2),则、关于抛物线的对称轴对称,
的坐标为,点的坐标为,,
当时(如图3),则是等腰直角三角形,,
过点作于点,设点的坐标为,
,,,解得,
.
9.如图,抛物线与坐标轴交点分别为,,,作直线BC.
求抛物线的解析式;
点P为抛物线上第一象限内一动点,过点P作轴于点D,设点P的横坐标为,求的面积S与t的函数关系式;
条件同,若与相似,求点P的坐标.
【答案】(1);(2);(3)点P的坐标为或
【解析】
设点P的坐标为,
,,
,
;
解得:或舍去,
,,
点P的坐标为,
综上所述点P的坐标为或
10.如图,抛物线的顶点坐标为,并且与轴交于点,与轴交于、两点.
()求抛物线的表达式.
()如图,设抛物线的对称轴与直线交于点,点为直线上一动点,过点作轴的平行线,与抛物线交于点,问是否存在点,使得以、、为顶点的三角形与相似.若存在,求出点的坐标;若不存在,请说明理由.
【答案】(1);(2)或或或.
【解析】试题分析:(1)设抛物线的表达式为y=a(x-2)2-1(a≠0),将点C的坐标代入即可得出答案;(2)由直线BC的解析式知,∠OBC=∠OCB=45°.又由题意知∠EFD=∠COB=90°,所以只有△EFD∽△COB,根据这种情况求点E的坐标即可.
试题解析:
()该抛物线的顶点坐标为,所以该抛物线的解析式为,又该抛物线过点,代入得:
,解得,故该抛物线的解析式为+3.
如图,连接DF.
当x=2-时,y=-x+3=1+;
∴E1(2-,1+)、E2(2+,1-).
∠EDF=90°;易知,直线AD:y=x-1,联立抛物线的解析式有:
x2-4x+3=x-1,解得 x1=1、x2=4;
当x=1时,y=-x+3=2;
当x=4时,y=-x+3=-1;
∴E3(1,2)、E4(4,-1).
∴综上,点E的坐标为(2-,1+)或(2+,1-)或(1,2)或(4,-1).
11.如图,在平面直角坐标系中,直线与坐标轴分别交于、两点,抛物线过、两点,点为线段上一动点,过点作轴于点,交抛物线于点.
求抛物线的解析式.
求面积的最大值.
连接,是否存在点,使得和相似?若存在,求出点坐标;若不存在,说明理由.
【答案】(1).(2)存在点,使得和相似,点的坐标为或.
【解析】
如图,连接、过点作轴于点,
设点坐标为,则点坐标为,
则,,
∵,
∴,
∵为等腰直角三角形,和相似
∴必为等腰直角三角形.
若,则,
∵,
∴,
∴,
∴.
∵点在抛物线上,
∴,解得(不合题意,舍去)或,
∴;
若,则,
在等腰直角三角形中,,
12.在平面直角坐标系中,抛物线与轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
【答案】(1),(-1,4) (2)(-2,3),,
(3)(-4,-5),(,)
【解析】
(1)设抛物线的解析式为,
∵抛物线过点A(-3,0),B(1,0),D(0,3),
∴,解得,a=-1,b=-2,c=3,
∴抛物线解析式为,顶点C(-1,4);
(3)①若点P在对称轴左侧(如图2),只能是△CPQ∽△ACH,得∠PCQ=∠CAH,
∴,
分别过点C、P作x轴的平行线,过点Q作y轴的平行线,交点为M和N,
由△CQM∽△QPN,
得=2,
∵∠MCQ=45°,
设CM=m,则MQ=m,PN=QN=2m,MN=3m,
∴P点坐标为(-m-1,4-3m),
将点P坐标代入抛物线解析式,得,
解得m=3,或m=0(与点C重合,舍去)
∴P点坐标为(-4,-5);
②若点P在对称轴右侧(如图①),只能是△PCQ∽△ACH,得∠PCQ=∠ACH,
∴,
13.抛物线过点和,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作,且,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
求抛物线解析式;
当点D落在抛物线上时,求点P的坐标;
若以A、B、D为顶点的三角形与相似,请直接写出此时t的值.
【答案】(1)抛物线的解析式为:;(2);(3)当、时,以A、B、D为顶点的三角形与相似.
【解析】
解:由题意得,
解得.
故抛物线的解析式为:;
假设在抛物线上,有,
解得 或,
,
,
即当时,点D落在抛物线上.
当时,如图1,
若∽,
∽,
∽,
,即,化简得:,
解得:.
,
.
当时,如图2,
解得负根舍去.
∽,
∽,同理,此时t无解.
综合上述:当、时,以A、B、D为顶点的三角形与相似.
14.如图,已知抛物线的对称轴为直线,( ),且经过、两点,与轴交于另一点,设是抛物线的对称轴上的一动点,且.
()求这条抛物线所对应的函数关系式.
()求点的坐标.
()探究坐标轴上是否存在点,使得、、为顶点的三角形与相似?若存在,请指出符合条件的点的位置,并直接写出点的坐标;若不存在,请说明理由.
【答案】(1);(2);(3), ,
()设经过点且与直线垂直的直线为直线,作轴,垂足为;
∵,
∴, ,
∴.
()连接,则容易得出,又,可知,得符合条件的点为.
15.如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.
(1)求抛物线的解析式及点M的坐标.
(2)点P是直线BC在y轴右侧部分图象上的动点,若点P,点C,点M所构成的三角形与△AOC相似,求符合条件的P点坐标.
(3)过点C作CD∥AB,CD交抛物线于点D,点Q是线段CD上的一动点,作直线QN与线段AC交于点N,与x轴交于点E,且∠BQE=∠BDC,当CN的值最大时,求点E的坐标.
【答案】 (1)y=x2-2x-3,M(1,-4);(2)P1(,-),P2(3,0);(3)E(-10,0).[来源:+网Z+X+X+K]
【解析】
(2)连接MC,作MF⊥y轴于点F,则点F坐标为(0,-4).
∵MF=1,CF=-3-(-4)=1,
∴MF=CF,MC=.
∴∠FCM=∠FMC=45°.
∵B(3,0),C(0,-3),∴OB=OC=3.
而∠BOC=90°,∴∠OCB=∠OBC=45°.
∴∠MCB=180°-∠OCB-∠FCM=90°.
由此可知,∠MCP=90°,则点O与点C必为相似三角形对应点.
过点P作PH⊥y轴于H.
①若有△PCM∽△AOC,则有=.
∴CP===.
∵∠PCH=45°,CP=,
∴PH=CH=÷=.
∴OH=OC-CH=3-=.
∴P1(,-);
(3)过点Q作QG⊥x轴于点G.
设点E的坐标为(n,0),Q的坐标为(m,-3).
∵CD∥x轴,
∴D的纵坐标为-3.
把y=-3代入y=x2-2x-3,
∴x=0或x=2.
∴D(2,-3).
∵B(3,0),
∴由勾股定理可求得:BD=.
∵Q(m,-3),
∴QD=2-m,CQ=m(0≤m≤2).
∵∠BQE=∠BDC,∠EQC+∠BQE=∠BDC+∠QBD,
∴∠EQC=∠QBD.
又由抛物线的轴对称性可知:∠NCQ=∠BDC,
∴△NCQ∽△QDB.
∴=.
∴=.
∴CN=-(m2-2m)=-(m-1)2+.
∴当m=1时,CN可取得最大值.此时Q的坐标为(1,-3).
∴BQ2=QD•EB,即13=1×(3-n),
∴n=-10.
∴E的坐标为(-10,0).
16.如图,在平面直角坐标系xOy中,将抛物线y=x2平移,使平移后的抛物线经过点A(–3,0)、B(1,0).
(1)求平移后的抛物线的表达式.
(2)设平移后的抛物线交y轴于点C,在平移后的抛物线的对称轴上有一动点P,当BP与CP之和最小时,P点坐标是多少?
(3)若y=x2与平移后的抛物线对称轴交于D点,那么,在平移后的抛物线的对称轴上,是否存在一点M,使得以M、O、D为顶点的三角形△BOD相似?若存在,求点M坐标;若不存在,说明理由.
【答案】(1)y=x2+2x﹣3;(2)点P坐标为(﹣1,﹣2);(3)点M坐标为(﹣1,3)或(﹣1,2).
【解析】
(2)∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线对称轴为直线x=﹣1,与y轴的交点C(0,﹣3),
则点C关于直线x=﹣1的对称点C′(﹣2,﹣3),
如图1,
连接B,C′,与直线x=﹣1的交点即为所求点P,
由B(1,0),C′(﹣2,﹣3)可得直线BC′解析式为y=x﹣1,
则,
解得,
所以点P坐标为(﹣1,﹣2);
(3)如图2,
∵∠BOD=135°,
∴点M只能在点D上方,
∵∠BOD=∠ODM=135°,
∴当或时,以M、O、D为顶点的三角形△BOD相似,
①若,则,解得DM=2,
此时点M坐标为(﹣1,3);
17.已知抛物线的图象经过点、,顶点为,与轴交于点.
求抛物线的解析式和顶点的坐标;
如图,为线段上一点,过点作轴平行线,交抛物线于点,当的面积最大时,求点的坐标;
如图,若点是直线上的动点,点、、所构成的三角形与相似,请直接写出所有点的坐标;
如图,过作轴于点,是轴上一动点,是线段上一点,若,则的最大值为________,最小值为________.
【答案】(1)抛物线解析式为y=−x2+2x+3,顶点坐标E(1,4).(2)P(,).(3)Q点坐标为(3,0),(−3,6), (,),(−,).(4)m的最大值为5,最小值为−54.
【解析】
(1)∵抛物线y=−x2+bx+c的图象经过点A(−1,0)、B(3,0),
∴,
解得,
∴抛物线解析式为y=−x2+2x+3,
顶点坐标E(1,4).
(2)如图1中,
∵−<0,
∴当a=时,△BDC的面积最大,此时P(,).
(3)如图2中,[来源:]
∵C(0,3),E(1,4),B(3,0),
∴直线EC的解析式为y=x+3,直线BC的解析式为y=−x+3,
∵1×(−1)=−1,
∴EC⊥BC,
∴∠ECB=90〬,
(4)如图3中,过C作CH⊥EF于H点,则CH=EH=1,
当M在EF左侧时,
∵∠MNC=90〬,
则△MNF∽△NCH,
∴,
作EM⊥CE交x轴于点M,则∠FEM=45〬,
∵FM=EF=4,
∴OM=5,
即N为点E时,OM=5,此时m的值最大,
∴m⩽5,
∴m的最大值为5,最小值为−54,
18.如图,已知抛物线的对称轴是y轴,且点(2,2),(1,)在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.
(1)求抛物线的解析式及顶点N的坐标;
(2)求证:四边形PMDA是平行四边形;
(3)求证:△DPE∽△PAM,并求出当它们的相似比为时的点P的坐标.
【答案】(1), N(0,1);(2)证明见解析;(3)证明见解析,P(,4)或(﹣,4).
【解析】
(3)解:同(2)设P(t,),则C(0,),PA=,PC=|t|,∵M(0,2),∴CM=﹣2=,在Rt△PMC中,由勾股定理可得PM= = = ==PA,且四边形PMDA为平行四边形,∴四边形PMDA为菱形,∴∠APM=∠ADM=2∠PDM,∵PE⊥y轴,且抛物线对称轴为y轴,∴DP=DE,且∠PDE=2∠PDM,∴∠PDE=∠APM,且,∴△DPE∽△PAM;∵OA=|t|,OM=2,∴AM=,且PE=2PC=2|t|,当相似比为时,则=,即 =,解得t=或t=﹣,∴P点坐标为(,4)或(﹣,4).[来源:ZXXK]
考点:二次函数综合题;压轴题.
19.如图1,抛物线 经过 , 两点,与 轴相交于点 ,连接 .点 为抛物线上一动点,过点 作 轴的垂线 ,交直线 于点 ,交 轴于点 .
Ⅰ 求抛物线的表达式;
Ⅱ 当 位于 轴右边的抛物线上运动时,过点 作 直线 , 为垂足.当点 运动到何处时,以 , , 为顶点的三角形与 相似?并求出此时点 的坐标;
Ⅲ 如图2,当点 在位于直线 上方的抛物线上运动时,连接 , .请问 的面积 能否取得最大值?若能,请求出最大面积 ,并求出此时点 的坐标;若不能,请说明理由.
【答案】(1)抛物线的表达式为 ;(2)点 的坐标为 或 ;(3)当 时, 的面积 能取最大值 ,此时 点坐标为 .
(2) 点坐标为 ,
为等腰直角三角形,且 为直角.
, , 为顶点的三角形与 相似,
为等腰直角三角形,
又 直线 ,
.
设 ,则 ,
.
,
,解得 或 .
点 的坐标为 或 .
20.如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】解(1)设抛物线的解析式为y=ax2+bx+c(a≠0),且过A(﹣2,0),B(﹣3,3),O(0,0)可得
,
解得.
故抛物线的解析式为y=x2+2x;
(3)存在,
如上图:∵B(﹣3,3),C(﹣1,﹣1),根据勾股定理得:
BO2=18,CO2=2,BC2=20,
∴BO2+CO2=BC2.
∴△BOC是直角三角形.
假设存在点P,使以P,M,A为顶点的 三角形与△BOC相似,
设P(x,y),由题意知x>0,y>0,且y=x2+2x,
【解析】略
专题04 因动点产生的相似、全等问题版突破中考数学压轴之学霸秘笈大揭秘(学生版): 这是一份专题04 因动点产生的相似、全等问题版突破中考数学压轴之学霸秘笈大揭秘(学生版),共12页。
专题01 因动点产生的面积问题-版突破中考数学压轴之学霸秘笈大揭秘(教师版): 这是一份专题01 因动点产生的面积问题-版突破中考数学压轴之学霸秘笈大揭秘(教师版),共46页。
专题14 因动点产生的面积问题-版突破中考数学压轴之学霸秘笈大揭秘 学生版+教师版: 这是一份专题14 因动点产生的面积问题-版突破中考数学压轴之学霸秘笈大揭秘 学生版+教师版,文件包含专题14图形变换和类比探究类几何压轴综合问题-版突破中考数学压轴之学霸秘笈大揭秘学生版doc、专题14图形变换和类比探究类几何压轴综合问题-版突破中考数学压轴之学霸秘笈大揭秘教师版doc等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。












