2020-2021学年广东省深圳市南山区第二外国语学校集团海德学校九上期末数学试卷

这是一份2020-2021学年广东省深圳市南山区第二外国语学校集团海德学校九上期末数学试卷，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
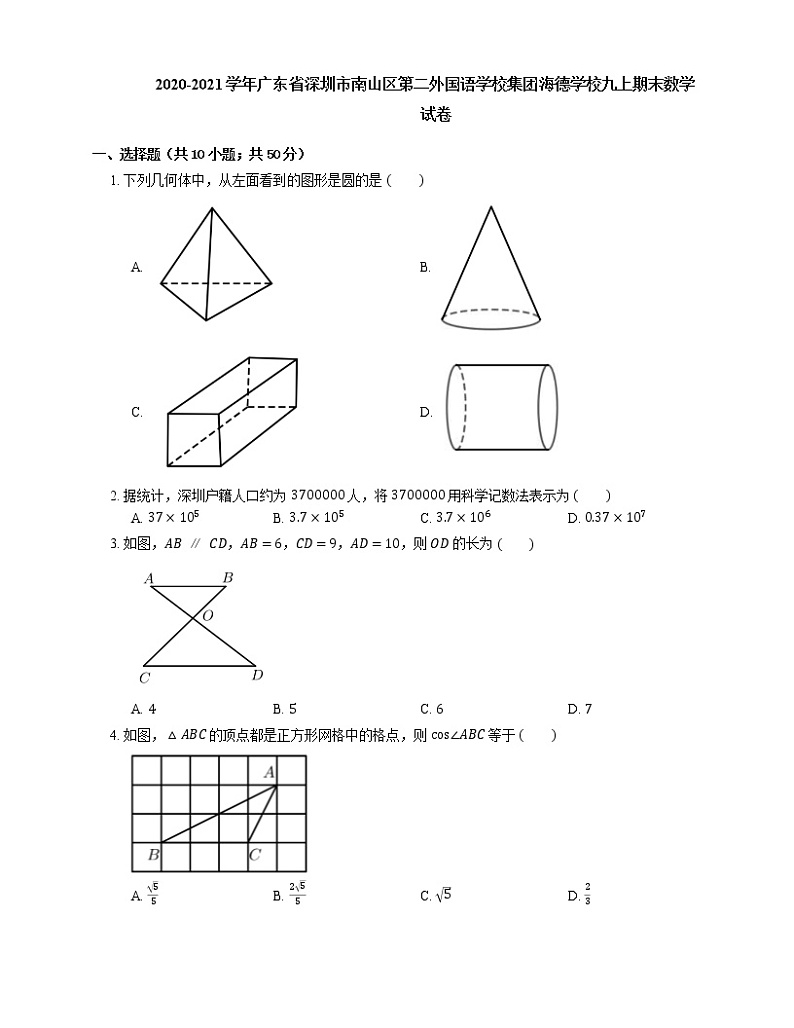
1. 下列几何体中，从左面看到的图形是圆的是
A. B.
C. D.

2. 据统计，深圳户籍人口约为 3700000 人，将 3700000 用科学记数法表示为
A. 37×105B. 3.7×105C. 3.7×106D. 0.37×107

3. 如图，AB∥CD，AB=6，CD=9，AD=10，则 OD 的长为
A. 4B. 5C. 6D. 7

4. 如图，△ABC 的顶点都是正方形网格中的格点，则 cs∠ABC 等于
A. 55B. 255C. 5D. 23

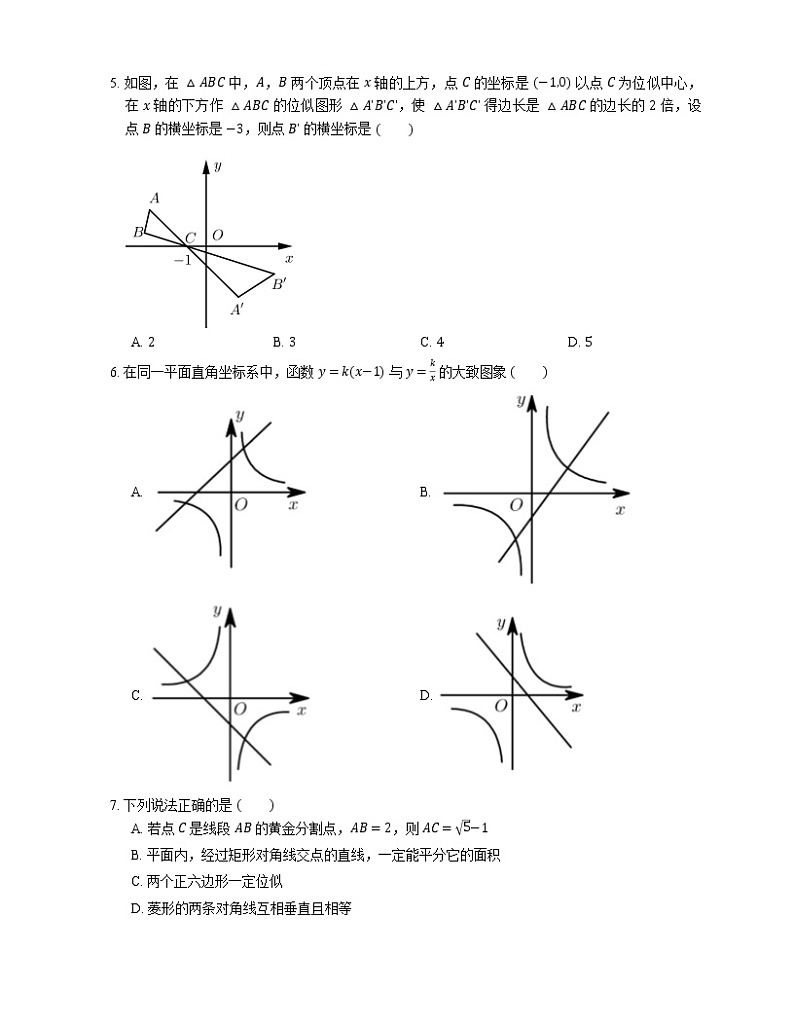
5. 如图，在 △ABC 中，A，B 两个顶点在 x 轴的上方，点 C 的坐标是 −1,0 以点 C 为位似中心，在 x 轴的下方作 △ABC 的位似图形 △AʹBʹCʹ，使 △AʹBʹCʹ 得边长是 △ABC 的边长的 2 倍，设点 B 的横坐标是 −3，则点 Bʹ 的横坐标是
A. 2B. 3C. 4D. 5

6. 在同一平面直角坐标系中，函数 y=kx−1 与 y=kx 的大致图象
A. B.
C. D.

7. 下列说法正确的是
A. 若点 C 是线段 AB 的黄金分割点，AB=2，则 AC=5−1
B. 平面内，经过矩形对角线交点的直线，一定能平分它的面积
C. 两个正六边形一定位似
D. 菱形的两条对角线互相垂直且相等

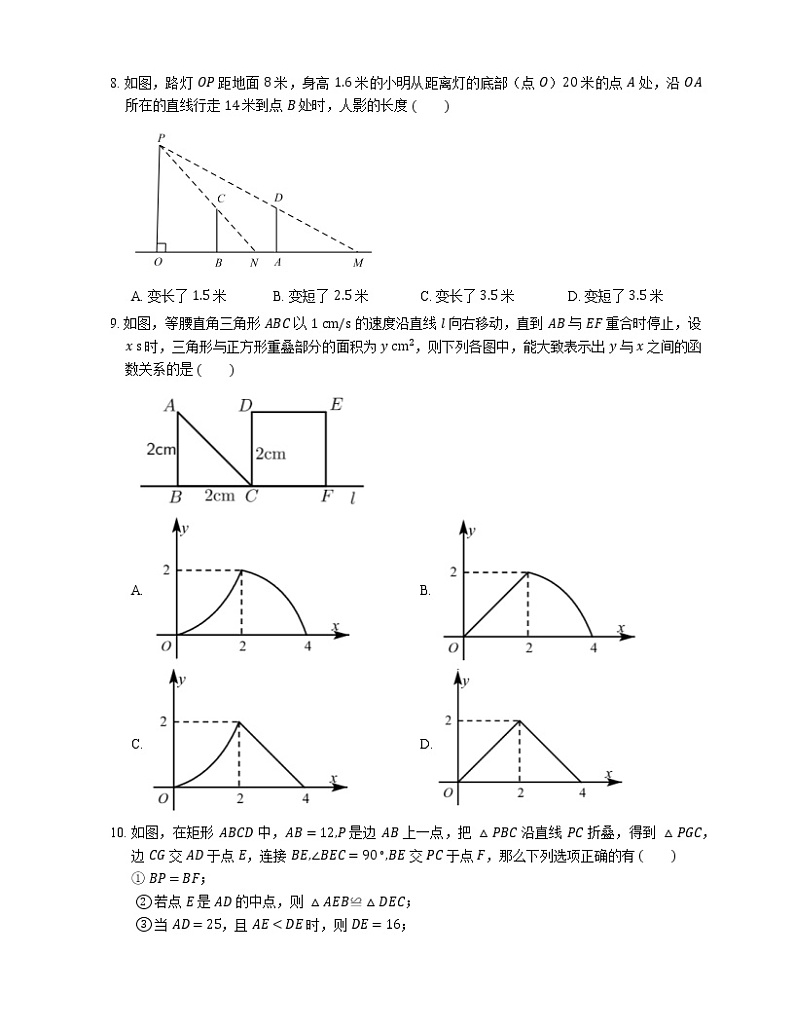
8. 如图，路灯 OP 距地面 8 米，身高 1.6 米的小明从距离灯的底部（点 O）20 米的点 A 处，沿 OA 所在的直线行走 14 米到点 B 处时，人影的长度
A. 变长了 1.5 米B. 变短了 2.5 米C. 变长了 3.5 米D. 变短了 3.5 米

9. 如图，等腰直角三角形 ABC 以 1 cm/s 的速度沿直线 l 向右移动，直到 AB 与 EF 重合时停止，设 x s 时，三角形与正方形重叠部分的面积为 y cm2，则下列各图中，能大致表示出 y 与 x 之间的函数关系的是
A. B.
C. D.

10. 如图，在矩形 ABCD 中，AB=12,P 是边 AB 上一点，把 △PBC 沿直线 PC 折叠，得到 △PGC，边 CG 交 AD 于点 E，连接 BE,∠BEC=90∘,BE 交 PC 于点 F，那么下列选项正确的有
① BP=BF；
② 若点 E 是 AD 的中点，则 △AEB≌△DEC；
③ 当 AD=25，且 AE ④ 当 AD=25，可得 sin∠PCB=31010；
⑤ 当 BP=9 时，BE⋅EF=108．
A. 5 个B. 4 个C. 3 个D. 2 个

二、填空题（共5小题；共25分）
11. 若 csA−12+tanB−3=0，那么 △ABC 的形状是 ．

12. 若关于 x 的一元二次方程 a+3x2+2x+a2−9=0 有一个根为 0，则 a 的值为 ．

13. 已知二次函数 y=x2+bx+4 顶点在 x 轴上，则 b= ．

14. 有两个全等矩形纸条，长与宽分别为 11 和 7，按如图所示的方式交叉叠放在一起，则重合部分构成的四边形 BGDH 的周长为 ．

15. 如图．已知，在矩形 AOBC 中，OB=4，OA=3．分别以 OB，OA 所在直线为 x 轴和 y 轴，建立如图所示的平面直角坐标系，F 是边 BC 上的一个动点（不与 B，C 重合），过 F 点的反比例函数 y=kxk>0 的图象与 AC 边交于点 E．将 △CEF 沿 EF 对折后，C 点恰好落在 OB 上的点 D 处，则 k 的值为 ．

三、解答题（共7小题；共91分）
16. 计算：∣1−2∣−13−1+2020−π0−2cs45∘．

17. 先化简，再求值：a+1a2−2a+1÷2+3−aa−1，其中 a=2．

18. 我区某中学为了解八年级学生的体能状况，从八年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级．请根据两幅统计图中的信息回答下列问题：
（1）本次抽样调查共抽取了多少名学生?
（2）求测试结果为C等级的学生数，并补全条形图．
（3）若该中学八年级共有 700 名学生，请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
（4）若从体能为A等级的 2 名男生 2 名女生中随机的抽取 2 名学生，做为该校培养运动员的重点对象，请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率．

19. 如图是一矩形广告牌 ACGE，AE=2 米，为测量其高度，某同学在 B 处测得 A 点仰角为 45∘，该同学沿 GB 方向后退 6 米到 F 处，此时测得广告牌上部灯杆顶端 P 点仰角为 37∘．若该同学眼睛离地面的垂直距离为 1.7 米，灯杆 PE 的高为 2.25 米，求广告牌的高度（AC 或 EG 的长）．（精确到 1 米，参考数据：sin37∘≈0.6，tan37∘≈0.75）

20. 在 2020 年新冠肺炎抗疫期间，小明决定在淘宝上销售一批口罩．经市场调研：某类型口罩进价每袋为 20 元，当售价为每袋 25 元时，销售量为 250 袋，若销售单价每提高 1 元，销售量就会减少 10 袋．
（1）直接写出小明销售该类型口罩销售量 y（袋）与销售单价 x（元）之间的函数关系式 ；每天所得销售利润 w（元）与销售单价 x（元）之间的函数关系式 ．
（2）若小明想每天获得该种类型口罩的销售利润为 2000 元时，则销售单价应定为多少元?
（3）若每天销售量不少于 100 袋，且每袋口罩的销售利润至少为 17 元，则销售单价定为多少元时，此时利润最大，最大利润是多少?

21. 在矩形 ABCD 的 CD 边上取一点 E，将 △BCE 沿 BE 翻折，使点 C 恰好落在 AD 边上点 F 处．
（1）如图 1，若 BC=2BA，求 ∠CBE 的度数．
（2）如图 2，当 AB=5，且 AF⋅FD=10 时，求 BC 的长．
（3）如图 3，延长 EF，与 ∠ABF 的角平分线交于点 M，BM 交 AD 于点 N，当 NF=AN+FD 时，求 ABBC 的值．

22. 如图，抛物线 y=ax2+94x+ca≠0 与 x 轴相交于点 A−1,0 和点 B．与 y 轴相交于点 C0,3，作直线 BC．
（1）求抛物线的解析式；
（2）在直线 BC 上方的抛物线上存在点 D，使 ∠DCB=2∠ABC，求点 D 的坐标；
（3）在（2）的条件下，点 F 的坐标为 0,72，点 M 在抛物线上，点 N 在直线 BC 上，当以 D，F，M，N 为顶点的四边形是平行四边形时，请直接写出点 N 的坐标．
答案
第一部分
1. D【解析】A选项：选项A中的几何体的左视图为三角形，故A错误；
B选项：选项B中的几何体其左视图为等腰三角形，故B错误；
C选项：选项C中的几何体的左视图为长方形，故C错误；
D选项：选项D中的几何体，其左视图为圆，故D正确．
2. C【解析】3700000=3.7×106．
3. C【解析】∵AB∥CD，
∴△AOB∽△DOC，
∴AOOD=ABCD=69=23，
∴AO=23OD，
∵AD=AO+OD=53OD=10，
∴OD=6．
4. B【解析】由格点可得 ∠ABC 所在的直角三角形的两条直角边为 2，4，
∴ 斜边为 22+42=25，
∴cs∠ABC=425=255．
5. B
【解析】作 BD⊥x 轴于 D，BʹE⊥x 轴于 E，
则 BD∥BʹE，
由题意得 CD=2，BʹC=2BC，
∵BD∥BʹE，
∴△BDC∽△BʹEC，
∴CDCE=BCBʹC=12，
∴CE=4，则 OE=CE−OC=3，
∴ 点 Bʹ 的横坐标是 3．
6. B【解析】因为函数 y=kx−1，无论 k 为何值，函数图象一定过 1,0 点，故排除选项A和选项C，
当 k>0 时，函数 y=kx−1 与 y=kx 都经过第一、三象限，
当 k<0 时，函数 y=kx−1 与 y=kx 都经过第二、四象限，
故排除选项D，只有选项B的图象符合．
7. B【解析】A、若点 C 是线段 AB 的黄金分割点，AB=2，当 AC>BC 时，AC=5−1，当 ACB、平面内，经过矩形对角线交点的直线，一定能平分它的面积，本选项说法正确；
C、两个正六边形不一定位似，本选项说法错误；
D、菱形的两条对角线互相垂直，但不一定相等，本选项说法错误；
故选：B．
8. D【解析】设小明在 A 处时影长为 x，B 处时影长为 y．
∵AD∥OP，BC∥OP，
∴△ADM∽△OPM，△BCN∽△OPN，
∴ADOP=MAMO，BCOP=BNON，
则 xx+20=1.68，
∴x=5．
yy+20−14=1.68，
∴y=1.5，
∴x−y=3.5，故变短了 3.5 米．
9. A【解析】如图 1 ，
当 x≤2 时，重叠部分为三角形，面积 y=12⋅x⋅x=12x2，
如图 2，
当 2≤x≤4 时，重叠部分为梯形，面积 y=12×2×2−12×x−22=−12x−22+4，
所以，图象为两段二次函数图象，纵观各选项，只有A选项符合．
10. B
【解析】① 在矩形 ABCD,∠ABC=90∘，
∵△BPC 沿 PC 折叠得到 △GPC，
∴∠PGC=∠PBC=90∘,∠BPC=∠GPC，
∵BE⊥CG，
∴BE∥PG，
∴∠GPF=∠PFB，
∴∠BPF=∠BFP，
∴BP=BF，
故 ① 正确；
② 在矩形 ABCD 中，∠A=∠D=90∘,AB=DC，
∵E 是 AD 中点，
∴AE=DE，
在 △ABE 和 △DCE 中，AB=DC,∠A=∠D=90∘,AE=DE,
∴△AEB≌△DECSAS，
故 ② 正确；
③ 当 AD=25 时，
∵∠BEC=90∘，
∴∠AEB+∠CED=90∘，
∵∠AEB+∠ABE=90∘，
∴∠CED=∠ABE，
∵∠A=∠D=90∘，
∴△ABE∽△DEC，
∴ABAE=DECD，
设 AE=x，
∴DE=25−x，
∴12x=25−x12，
∴x=9 或 x=16，
∵AE ∴AE=9,DE=16，故 ③ 正确；
④ 由 ③ 知：
CE=DE2+CD2=162+122=20，
BE=AE2+AB2=92+122=15，
由折叠得，BP=PG，
∴BP=BF=PG，
∵BE∥PG，
∴△ECF∽△GCP，
∴EFPG=ECCG，
设 BP=BF=PG=y，
∴15−yy=2025，
∴y=253，
∴BP=253，
在 Rt△PBC 中，
PC=PB2+BC2=2532+252=25310.
∴sin∠PCB=PBPC=25325310=1010，
故 ④ 不正确；
⑤ 如图，连接 FG，
由 ① 知 BF∥PG，
∵BF=PG=PB，
∴ 平行四边形 BPGF 是菱形，
∴BP∥GF,FG=PB=9，
∴∠GFE=∠ABE，
∴△GEF∽△EAB，
∴EFAB=GFBE，
∴BE⋅EF=AB⋅GF=12×9=108，
故 ⑤ 正确，
所以本题正确的有 ①②③⑤,4 个，
故选B．
第二部分
11. 等边三角形
【解析】由题意可知，csA=12，则 ∠A=60∘，
tanB=3，则 ∠B=60∘，
∴∠C=180∘−∠A−∠B=60∘．
12. 3
【解析】根据题意，将 x=0 代入方程可得 a2−9=0，
解得：a=3 或 a=−3，
∵a+3≠0，即 a≠−3，
∴a=3．
故答案为：3．
13. ±4
【解析】∵ 二次函数 y=x2+bx+4 的顶点在 x 轴上，
∴Δ=b2−4ac=b2−4×1×4=0，
∴b2=16，
∴b=±4．
14. 34011
【解析】∵ 图中是矩形纸条，
∴DE∥BF，BC∥AD，
∴ 四边形 BGDH 是平行四边形，
在 △ABH 和 △FDH 中，
∠BAH=∠DFH=90∘,∠BHA=∠DHF,AB=DF,
∴△ABH≌△FDH，
∴BH=DH，
∴ 四边形 BGDH 是菱形，
∴DG=BG=BH=DH，
设 DG=BG=x，则 EG=11−x，
在 Rt△EGB 中，EG2+BE2=BG2，
∴72+11−x2=x2，
整理得 49+121−22x+x2=x2，
解得 x=8511，
∴ 四边形 BGDH 的周长为 4×8511=34011．
15. 218
【解析】∵ 将 △CEF 沿 EF 对折后，C 点恰好落在 OB 上的 M 点处，
∴∠EMF=∠C=90∘，EC=EM，CF=MF，
∴∠DME+∠FMB=90∘，而 ED⊥OB，
∴∠DME+∠DEM=90∘，
∴∠DEM=∠FMB．
∴Rt△DEM∽Rt△BMF；
又 ∵EC=AC−AE=4−k3，CF=BC−BF=3−k4，
∴EM=4−k3，MF=3−k4，
∴EMMF=4−k33−k4=43；
∴ED:MB=EM:MF=4:3，而 ED=3，
∴MB=94，
在 Rt△MBF 中，MF2=MB2+MF2，
即 3−k42=942+k42，解得 k=218．
第三部分
16. ∣1−2∣−13−1+2020−π0−2cs45∘=2−1−3+1−2×22=2−1−3+1−2=−3.
17. 原式=a+1a−12÷2a−2+3−aa−1=a+1a−12÷a+1a−1=a+1a−12×a−1a+1=1a−1,
当 a=2 时，原式 =12−1=1．
18. （1） 10÷20%=50，
所以本次抽样调查共抽取了 50 名学生．
（2） 测试结果为C等级的学生数为 50−10−20−4=16（人），
补全条形图如图所示：
（3） 700×450=56，
所以估计该中学八年级学生中体能测试结果为D等级的学生有 56 名．
（4） 画树状图为：
共有 12 种等可能的结果数，其中抽取的两人恰好都是男生的结果数为 2，
所以抽取的两人恰好都是男生的概率 =212=16．
19. 如图，延长 HD 交 AC，BG 于点 M，N，
则由题意可知 MG=NC=DB=HF=1.7（米），
MN=AE=2（米），
∵ 在 Rt△AND 中，∠ADN=45∘，
∴AN=DN，
∴ 设 AN=DN=x（米），
则 EM=AN=x，
∴PM=EM+PE=x+2.25（米），
MH=MN+ND+DH=2+x+6=x+8（米），
∵ 在 Rt△PHM 中，∠PHM=37∘，
∴tan∠PHM=PMMH，
即 tan37∘=x+2.25x+8=0.75，
∴ 解得：x=15，
∴EM=15（米），
∴EG=EM+MG=15+1.7=16.7≈17（米），
∴ 广告牌的高度为 17 米．
20. （1） y=−10x+500；w=−10x2+700x−10000
【解析】y=250−10x−25=−10x+500，
则 w=x−20−10x+500=−10x2+700x−10000．
（2） ∵w=2000，
∴−10x2+700x−10000=2000，
解得 x1=30，x2=40．
答：销售单价为 30 元或 40 元时，小明每天获得该种类型口罩的销售利润为 2000．
（3） 由题意得 −10x+500≥100,x−20≥17,
∴x 的取值范围为：37≤x≤40．
∵ 函数 w=−10x−352+2250，对称轴为直线 x=35，
∴ 当 x=37 时，w最大值=1850．
21. （1） 由 △BCE 翻折得到 △BFE 可知：BC=BF，∠CBE=∠FBE．
又 ∵BC=2BA=BF，
∴ 在 Rt△ABF 中，
cs∠ABF=ABBF=AB2AB=12，
可得：∠ABF=60∘，
∴∠CBF=90∘−60∘=30∘．
又 ∵∠CBE=∠FBE=12∠CBF，
故可得 ∠CBE=12×30∘=15∘．
（2） 由翻折可知：∠BFE=∠BCE=90∘，
∴ 可得 ∠AFB+∠DFE=90∘．
又 ∵ 在 △AFB 中，∠AFB+∠ABF=90∘，
在 Rt△DEF 中，∠DFE+∠DEF=90∘，
故可得 ∠DFE=∠ABF，∠AFB=∠DEF，
∴△AFB∽△DEF，
∴ABDF=AFDE，
故 AB⋅DE=AF⋅DF，即 5⋅DE=10，
∴DE=2，
∴EF=CE=5−2=3．
设 DF 为 a，在 Rt△DEF 中，a2+DE2=EF2，
即 a2+4=9，可得 DF=5．
又 ∵AF⋅DF=10，
∴AF=25，
故 BC=AD=AF+DF=25+5=35．
（3） 如图，过 N 点作 NH⊥BF 于 H 点．
∵∠NFH=∠BFA，∠NHF=∠BAF=90∘，
∴△NFH∽△BFA，
故 NHBA=FHFA=NFBF．
又 ∵NF=AN+FD，
即 NF=12AD=12BC=12BF，
即 NHBA=FHFA=NFBF=12BFBF=12，
设 NH=a，
又 ∵BN 为角平分线，NA⊥AB，NH⊥BF，
∴AN=HN=a．
在 Rt△ABN 和 Rt△HBN 中，
AN=HN,BN=BN,
∴Rt△ABN≌Rt△HBNHL，
故 BH=AB=2NH=2a．
设 FN=b，由 FHFA=FHa+b=12，
可得 FH=12a+b．
在 Rt△NHF 中，
由 NH2+FH2=FN2 得：a2+a+b22=b2，解得 b=53a，
∴BF=BH+HF=2a+a+53a2=103a，
故 ABBC=ABBF=2a103a=35．
22. （1） ∵ 抛物线 y=ax2+94x+c 经过点 A−1,0，B0,3，
∴a−94+c=0,c=3, 解得 a=−34,c=3,
∴ 抛物线的解析式为 y=−34x2+94x+3．
（2） 过点 C 作 CE∥x轴 交抛物线于点 E，则 ∠ECB=∠ABC，
过点 C 作 ∠DCE=∠ABC 交抛物线于点 D，
过点 D 作 DH⊥CE 于点 H，则 ∠DHC=90∘，
∴∠DCB=∠DCE+∠ECB=2∠ABC，
∵∠DHC=∠COB=90∘，∠DCH=∠ABC，
∴△DCH∽△CBO，
∴DHCO=CHBO，
设点 D 的横坐标为 t，则 Dt,−34t2+94t+3，
∵C0,3，
∴DH=−34t2+94t，
∵ 点 B 是 y=−34x2+94x+3 与 x 轴的交点，
∴−34x2+94x+3=0，
解得 x1=4，x2=−1，
∴B 的坐标为 4,0，
∴OB=4，
∴−34t2+94t3=t4，
解得 t1=0（舍去），t2=2，
∴ 点 D 的纵坐标为：−34t2+94t+3=92，
则点 D 坐标为 2,92．
（3） N163,3−64，N2−63,3+64，
N34+663,−664，N44−663,664．