2020-2021学年北京市西城区中考一模数学试卷

这是一份2020-2021学年北京市西城区中考一模数学试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
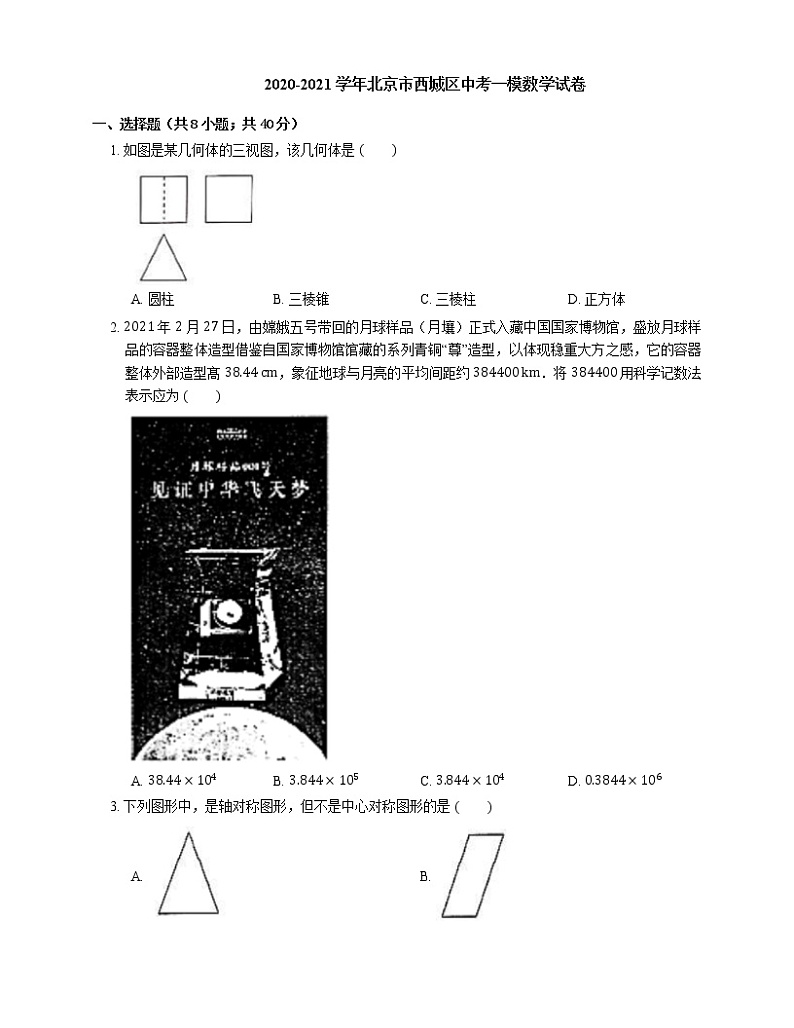
1. 如图是某几何体的三视图，该几何体是
A. 圆柱B. 三棱锥C. 三棱柱D. 正方体

2. 2021 年 2 月 27 日，由嫦娥五号带回的月球样品（月壤）正式入藏中国国家博物馆，盛放月球样品的容器整体造型借鉴自国家博物馆馆藏的系列青铜“尊”造型，以体现稳重大方之感，它的容器整体外部造型髙 38.44 cm，象征地球与月亮的平均间距约 384400 km．将 384400 用科学记数法表示应为
A. 38.44×104B. 3.844×105C. 3.844×104D. 0.3844×106

3. 下列图形中，是轴对称图形，但不是中心对称图形的是
A. B.
C. D.

4. 若实数 a，b 在数轴上的对应点的位置如图所示，则以下结论正确的是
A. a−b>0B. ab>0C. b>−aD. a<2b

5. 如果一个多边形的内角和等于它的外角和的 2 倍，那么这个多边形的边数是
A. 4B. 5C. 6D. 8

6. 如图，AB 是 ⊙O 的直径，CD 是弦（点 C 不与点 A，点 B 重合，且点 C 与点 D 位于直径 AB 两侧），若 ∠AOD=110∘，则 ∠BCD 等于
A. 25∘B. 35∘C. 55∘D. 70∘

7. 春回大地万物生，“微故宫”微信公众号设计了互动游戏，与大家携手走过有故宫猫陪伴的四季．游戏规则设计如下：每次在公众号对话框中回复【猫春图】，就可以随机抽取 7 款“猫春图”壁纸中的一款，抽取次数不限，假定平台设置每次发送每款图案的机会相同，小春随机抽取了两次，她两次都抽到“东风纸鸢”的概率是
A. 17B. 27C. 149D. 249

8. 风寒效应是一种因刮风所引起的使体感温度较实际气温低的现象，科学家提出用风寒温度描述刮风时的体感温度，并通过大量实验找出了风寒温度和风速的关系．下表中列出了当气温为 5∘C 时，风寒温度 T∘C 和风速 vkm/h 的几组对应值，那么当气温为 5∘C 时，风寒温度 T 与风速 v 的函数关系最可能是
风速v单位:km/h010203040风寒温度T单位:∘C531−1−3
A. 正比例函数关系B. 一次函数关系
C. 二次函数关系D. 反比例函数关系

二、填空题（共8小题；共40分）
9. 若分式 x−3x+2 的值为 0，则实数 x 的值为 ．

10. 将一副直角三角板如图摆放，点 A 落在 DE 边上，AB∥DF，则 ∠1= ∘．

11. 比 7 大的整数中，最小的是 ．

12. 如图所示的网格是正方形网格，A，B，C，D 是网格线的交点，那么 ∠DAC 与 ∠ACB 的大小关系为：∠DAC ∠ACB（填“>”，“=”或“<”）．

13. 已知方程组 2x+y=5,x+2y=1, 则 x+y 的值为 ．

14. 某公司销售一批新上市的产品，公司收集了这个产品 15 天的日销售额的数据，制作了如下的统计图．
关于这个产品销售情况有以下说法：
①第 1 天到第 5 天的日销售额的平均值低于第 6 天到第 10 天的日销售额的平均值；
②第 6 天到第 10 天日销售额的方差小于第 11 天到第 15 天日销售额的方差；
③这 15 天日销售额的平均值一定超过 2 万元．
所有正确结论的序号是 ．

15. 将二次函数 y=x2 的图象向右平移 3 个单位得到一个新函数的图象，请写出一个自变量 x 的取值范围，使得在所写的取值范围内，上述两个函数中，恰好其中一个函数的图象从左往右上升，而另一个函数的图象从左往右下降，写出的 x 的取值范围是 ．

16. 某商家需要更换店面的瓷砖，商家打算用 1500 元购买彩色和单色两种地砖进行搭配，并且把 1500 元全部花完．已知每块彩色地砖 25 元，每块单色地砖 15 元，根据需要，购买的单色地砖数要超过彩色地砖数的 2 倍，并且单色地砖数要少于彩色地砖数的 3 倍，那么符合要求的一种购买方案是 ．

三、解答题（共12小题；共156分）
17. 计算：4sin60∘+−13−2−12+∣−5∣．

18. 解不等式组 5x+1>7x−1,x−13>x−24. 并求它的整数解．

19. 已知 x2+3x−4=0，求代数式 2x+12x−1−3xx−1 的值．

20. 阅读材料并解决问题：
已知：如图，∠AOB 及内部一点 P．
求作：经过点 P 的线段 EF，使得点 E，F 分别在射线 OA，OB 上，且 OE=OF．
作法：如图．
①以点 O 为圆心，以任意长为半径作弧，分别交射线 OA，OB 于点 M，N；
②连接 NP，作线段 MP 的垂直平分线，得到线段 NP 的中点 C；
③连接 MC 并在它的延长线上截取 CD=MC；
④作射线 DP，分别交射线 OB，OA 于点 F，E．线段 EF 就是所求作的线段．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明证明：连接 MN．
由②得，线段 CN CP（填“>”，“=”或“<”）．
在 △MCN 和 △DCP 中，
, , ,
∴△MCN≌△DCP．
∠NMC=∠PDC．
∵.MN∥EF（ ）（填推理的依据）．
又由①得，线段 OM=ON．
可得 OE=OF．

21. 奥林匹克森林公园南园（奥森南园）是深受北京长跑爱好者追捧的跑步地点．小华和小萓相约去奥森南园跑步踏青，奥森南园有 5 千米和 3 千米的两条跑道（如图所示）．小华选择了 5 千米的路线，小萓选择了 3 千米的路线，已知小华平均每分钟比小萱平均每分钟多跑 100 米，两人同时出发，结果同时到达终点．求小萱的速度．

22. 如图，在平行四边形 ABCD 中，点 E 在 BC 的延长线上，CE=DE=2BC，DC 的中点为 F，DE 的中点为 G，连接 AF，FG．
（1）求证：四边形 AFGD 为菱形；
（2）连接 AG，若 BC=2，tanB=32，求 AG 的长．

23. 在平面直角坐标系 xOy 中，直线 y=−x+b 与双曲线 y=kxk≠0 交于 A，B 两点，点 A，点 B 的横坐标 xA，xB 满足 xA>xB，直线 y=−x+b 与 x 轴的交点为 C3,0，与 y 轴的交点为 D．
（1）求 b 的值；
（2）若 xA=2，求 k 的值；
（3）当 AD≥2BD 时，直接写出 k 的取值范围．

24. 国家大力提倡节能减排和环保，近年来纯电动汽车普及率越来越高，纯电动汽车的续航里程是人们选择时参考的重要指标．某汽车杂志根据当前汽车行业常用的两种续航里程测试标准（标准 M 和标准 N），对市面上常见的 9 种车型进行了续航里程实测，并与这些厂家公布的工信部续航里程进行了对比，下面是部分信息：
a．标准 M 下的实测续航里程数据为 324.8，355.8，378.2，385，403.7，407.9，441.2，445，463.2（单位：km）；
b．标准 N 下实测续航里程与工信部续航里程情况统计图（图 1）；
c．标准 N 下实测续航里程频数分布直方图，为方便记录，将续航里程设为 x（单位：km），数据分为A ∼ F六组（图 2）．
不同标准下实测续航里程统计表（单位：km）
标准M下实测续航里程标准N下实测续航里程平均数400.5316.6中位数ab
根据信息回答以下问题：
（1）补全图 2；
（2）不同标准下实测续航里程统计表中，a= ，在A ∼ F六组数据中，b 所在的组是 （只填写A ∼ F中的相应代号即可）；
判断 a 与 b 的大小关系为 a b（填“>”，“=”或“<”）．
（3）在选购纯电动汽车时，实测续航里程与工信部续航里程的比值（简称“续航里程达成比”）越高越好，但续航里程达成比受到实测时各种实际条件的限制只能达到一定比例，晓春打算为家里选购纯电动汽车，如果在标准 N 下，他希望续航里程达成比不低于 75%，请在图 1 中圈出实测续航里程不低于 300 km 的车型中，符合他要求的车型所对应的点．

25. 如图，AB 为 ⊙O 的弦，C 为 AB 的中点，D 为 OC 延长线上一点，DA 与 ⊙O 相切，切点为 A，连接 BO 并延长，交 ⊙O 于点 E，交直线 DA 于点 F．
（1）求证：∠B=∠D；
（2）若 AF=42，sinB=13，求 ⊙O 的半径．

26. 在平面直角坐标系 xOy 中，抛物线 y=ax2−2a2x+1a≠0 与 y 轴交于点 A，过点 A 作 x 轴的平行线与抛物线交于点 B．
（1）直接写出抛物线的对称轴；
（2）若 AB=4，求抛物线所对应的函数解析式；
（3）已知点 Pa+4,1，Q0,a+1，如果抛物线与线段 PQ 恰有一个公共点，结合函数图象，求 a 的取值范围．

27. 如图，在 △ABC 中，AB=AC，∠BAC>90∘，D 是 △ABC 内一点，∠ADC=∠BAC．过点 B 作 BE∥CD 交 AD 的延长线于点 E．
（1）依题意补全图形；
（2）求证：∠CAD=∠ABE；
（3）在（1）补全的图形中，不添加其他新的线段，在图中找出与 CD 相等的线段并加以证明．

28. 对于平面直角坐标系 xOy 中的线段 PQ，给出如下定义：若存在 △PQR 使得 S△PQR=PQ2，则称 △PDR 为线段 PQ 的“等幂三角形”，点 R 称为线段 PQ 的“等幂点”．
（1）已知 A3,0．
①在点 P11,3，P22,6，P3−5,1，P43,−6 中，是线段 OA 的“等幂点”的是 ；
②若存在等腰 △OAB 是线段 OA 的“等幂三角形”，求点 B 的坐标；
（2）已知点 C 的坐标为 C2,−1，点 D 在直线 y=x−3 上，记图形 M 为以点 T1,0 为圆心，2 为半径的 ⊙T 位于 x 轴上方的部分．若图形 M 上存在点 E，使得线段 CD 的“等幂三角形”△CDE 为锐角三角形，直接写出点 D 的横坐标 xD 的取值范围．
答案
第一部分
1. C
2. B
3. A
4. D
5. C
6. B
7. C
8. B
第二部分
9. 3
10. 75
11. 3
12. >
13. 2
14. ①②③
15. 答案不唯一，如：016. 答案不唯一，如：购买 24 块彩色地砖，60 块单色地砖
第三部分
17. 原式=4×32+9−23+5=23+9−23+5=14.
18. 原不等式组为
5x+1>7x−1, ⋯⋯①x−13>x−24. ⋯⋯②
解不等式①，得
x<3.
解不等式②，得
x>−2.∴
原不等式组的解集为
−2 原不等式组的整数解为 −1，0，1，2．
19. 2x+12x−1−3xx−1=4x2+3x−1=x2+3x−1,
∵x2+3x−4=0，
∴x2+3x=4，
∴原式=x2+3x−1=4−1=3．
20. （1） 补全的图形如图 1 所示．
（2） =；CN=CP；∠MCN=∠DCP；CM=CD；内错角相等，两直线平行
21. 设小萱的速度为 x 米/分．
则小华的速度为 x+100 米/分．
由题意得
5000x+100=3000x.
整理，得
5x=3x+100.
解得
x=150.
经检验，x=150 是原方程的解，且符合题意.
答：小萱的速度为 150 米/分．
22. （1） 因为四边形 ABCD 为平行四边形，点 E 在 BC 的延长线上，
所以 AD∥BE，AD=BC，
因为 DC 的中点为 F，DE 的中点为 G，
所以 FG∥CE，FG=12CE．
所以 AD∥FG．
又因为 CE=2BC，
所以 BC=12CE，
所以 AD=12CE，
所以 AD=FG，
所以四边形 AFGD 为平行四边形．
因为 FG=12CE，DG=12DE，CE=DE．
所以 FG=DG．
所以四边形 AFGD 为菱形．
（2） 如图，设 AG 与 DF 的交点为 O．
因为四边形 AFGD 为菱形，
所以 AG⊥DF，AG=2AO，
因为四边形 ABCD 为平行四边形，BC=2，tanB=32，
所以 AD=BC=2，tan∠1=tanB=32，
在 Rt△AOD 中，∠AOD=90∘，AD=2，tan∠1=32，
若设 AO=3k，则 OD=2k，AD=AO2+OD2=13k，
所以 13k=2，
解得 k=21313．
所以 AG=2AO=6k=121313．
23. （1） ∵ 直线 y=−x+b 与 x 轴的交点为 C3,0，
∴0=−3+b，
∴b=3．
（2） 由（1）得直线 y=−x+3
∵ 直线 y=−x+3 与双曲线 y=kxk≠0 的一个交点为 A，xA=2，
∴ 点 A 的坐标为 2,1，
∴1=k2，
解得 k=2．
（3） 024. （1） 由图 1 可得，C组的频数为 4，D组的频数为 1，
补全的图 2 如图所示；
（2） 403.7；C；>
【解析】∵ 标准 M 下的实测续航里程数据为 324.8，
355.8，378.2，385，403.7，407.9，441.2，445，463.2，
∴a=403.7，
由图 1 可知，b 在C组，
a>b，
故答案为：403.7，C，>；
（3） 由图 1 可知，不低于 300 km 的车型中对应的实际续航里程各数据约为：330，300，350，330，380，440，相对应的工程部续航里程为：410，440，475，510，525，570，相对应的“续航里程达成比”为：
330÷410≈80%，300÷440≈68%，
350÷475≈74%，330÷510≈65%，
380÷525≈72%，440÷570≈77%，
符合晓春要求的车型所对应的点如下图所示．
25. （1） 如图，连接 OA．
∵DA 与 ⊙O 相切，切点为 A，OA 为 ⊙O 的半径，
∴DA⊥OA，
∴∠OAD=90∘，∠1+∠CAD=90∘，
∵OA=OB，C 为 AB 的中点，
∴OC⊥BC，∠1=∠B．
∴∠D+∠CAD=90∘，
∴∠1=∠D，
∴∠B=∠D．
（2） 如图，连接 AE，
设 ⊙O 的半径为 r，
∵O 为 BE 的中点，C 为 AB 的中点，
∴AE∥OC，OC=12AE，
∴FAFD=AEOD，
∵∠B=∠D，sinB=13，
∴sinD=sin∠1=sinB=13，
在 Rt△OAD 中，OD=OAsinD=3r，AD=OD2−OA2=22r，
在 Rt△OAC 中，OC=OA⋅sin∠1=13r，
∴AE=2OC=23r．
∵AF=42，
∴2242+22r=23r3r，
化简，得 44+2r=29，
解得 r=7．
经检验，r=7 是原方程的解．
∴r=7．
26. （1） x=a．
（2） ∵ 抛物线 y=ax2−2a2x+1a≠0 与 y 轴的交点为 A．
∴ 点 A 的坐标为 A0,1．
∵ 过 A 所作 x 轴的平行线与抛物线的交点为 B，AB=4，
∴ 点 B 的坐标为 4,1 或 −4,1．
∴ 抛物线的对称轴为直线 x=2 或 x=−2．
∴a=2 或 a=−2．
∴ 抛物线所对应的函数解析式为 y=2x2−8x+1 或 y=−2x2−8x+1．
（3） ∵ 过 A 所作 x 轴的平行线与抛物线 y=ax2−2a2x+1a≠0 的交点为 B，
∴ 点 B 的纵坐标为 1．
∵ 点 B 的横坐标是关于 x 的方程 ax2−2a2x+1=1 的解．
解得 x1=0，x2=2a，
∴ 点 B 的坐标为 B2a,1．
又 ∵ 点 P 的坐标为 Pa+4,1．
∴ 点 P 在直线 AB 上．
①如图 1，
当 a>0 时，2a>0，a+1>1，a+4>a，
∴B2a,1 在 A0,1 右侧，且 Q0,a+1 在 y 轴上 N0,1 的上方，
Pa+4,1 在抛物线的对称轴右侧，
∵ 抛物线 y=ax2−2α2x+1a≠0 与线段 PQ 恰有一个公共点，
∴ 结合图象可得，点 P，点 B 的横坐标 x 满足 xP，
xB 满足 xP≥xB，
∴a>0，
a+4≥2a,
解得 0②如图 2，
当 a<0 时，2a<0，a+1<1，
a+4>a，
∴B2a,1 在 A0,1 左侧，且 Q0,a+1 在 y 轴上 A0,1 的下方，Pa+4,1 在抛物线的对称轴右侧．
∵ 拋物线 y=ax2−2a2x+1a≠0 与线段 PQ 恰有一个公共点，
∴ 结合图象可得，点 P，点 A 的横坐标 xP，
xA 满足 xP≥xA，
∴a<0，
a+4≥0，
解得 −4≤a<0，
综上所述，−4≤a<0 或 0≤a<4．
27. （1） 补全图形如图所示．
（2） 如图 1，延长 BE 至点 F．
∵BE∥CD，点 F 在 BE 的延长线上，
∴∠ADC=∠1．
∵∠ADC=∠BAC，
∴∠1=∠BAC，
∵∠1 是 △ABE 的外角，
∴∠1=∠ABE+∠BAE，
∴∠ABE=∠1−∠BAE．
又 ∵∠CAD=∠BAC−∠BAE，
∴∠CAD=∠ABE．
（3） AE．
如图 2，延长 BE 至点 F，在 BE 上截取 BG=AD，连接 AG．

由（2）得 ∠ABG=∠CAD，
又 ∵△ABG≌△CAD，
∴AG=CD，∠BGA=∠ADC，
∵∠ADC=∠1，
∴∠1=∠BGA，
∵∠AGE+∠BGA=180∘，∠2+∠1=180∘，
∴∠AGE=∠2，
∴AE=AG．
∴AE=CD．
28. （1） ① P2，P4；
②如图，
∵△OAB 是线段 OA 的“等幂三角形”，
∴S△OAB=OA2，
∵ 点 A 的坐标 A3,0，
若记 △OAB 中 OA 边上的高为 h，
则有 S△OAB=12×OA×h=32h=9，
解得则有 h=6，
∴ 点 B 在直线 y=6 或 y=−6 上，
∴△OAB 是等腰三角形，
∴ 点 B 在半径为 3 的 ⊙O，半径为 3 的 ⊙A 或线段 OA 的垂直平分线上，
综上所述，点 B 的坐标为 32,6 或 32,−6．
（2） 3−22