2020-2021学年天津市南开区八下期末数学试卷

这是一份2020-2021学年天津市南开区八下期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 如图，x 轴、 y 轴上分别有两点 A3,0，B0,2，以点 A 为圆心，AB 为半径的弧交 x 轴负半轴于点 C，则点 C 的坐标为
A. −1,0B. 2−5,0C. 1−132,0D. 3−13,0

2. 关于 x 的一元二次方程 k+3x2+5x+k2+2k−3=0 的一个根是 0，则 k 的值是
A. −3 或 1B. 1C. −3D. −1

3. 一家鞋店在一段时间内销售了某种女鞋 30 双，各种尺码的鞋销售量如下表：
尺码销售量/双12510462
店主决定在下次进货时增加一些 23.5 cm 尺码的女鞋，影响店主决策的统计量是
A. 平均数B. 中位数C. 众数D. 方差

4. 已知关于 x 的一元二次方程 x2−2m−1x+m2=0 有实数根，则 m 的取值范围是
A. m≠0B. m≤14C. m＜14D. m＞14

5. △ABC 中，∠A，∠B，∠C 的对边分别记为 a，b，c，由下列条件不能判定 △ABC 为直角三角形的是
A. ∠A+∠B=∠CB. ∠A:∠B:∠C=3:4:5
C. a2=c2−b2D. a:b:c=3:4:5

6. 如图，在四边形 ABCD 中，对角线 AC，BD 相交于点 O，下列条件不能判定这个四边形是平行四边形的是

A. AB∥DC，AD∥BCB. AB∥DC，∠DAB=∠DCB
C. AO=CO，AB=DCD. AB∥DC，DO=BO

7. 已知点 −2,y1，3,y2 都在直线 y=−x−5 上，则 y1，y2 的值的大小关系是
A. y1y2C. y1=y2D. 不能确定

8. 在平面直角坐标系 xOy 中，Rt△AOB 的直角顶点 B 在 y 轴上，点 A 的坐标为 1,3，将 Rt△AOB 沿直线 y=−x 翻折，得到 Rt△AʹOBʹ，过 Aʹ 作 AʹC 垂直于 OAʹ 交 y 轴于点 C，则点 C 的坐标为
A. 0,−23B. 0,−3C. 0,−4D. 0,−43

9. 如图，在菱形 ABCD 中，AB＝8，∠BAD=120∘，点 O 是对角线 BD 的中点，OE⊥CD 于点 E，则 OE 的长为
A. 23B. 3C. 4D. 2

10. 某组数据方差计算公式为：s2=22−x2+33−x2+24−x2n，由公式提供的信息，下列说法错误的是
A. 样本的容量是 3B. 样本的中位数是 3
C. 样本的众数是 3D. 样本的平均数是 3

11. 某药品经过两次降价，每瓶零售价由 168 元降为 108 元，已知两次降价的百分率相同．设每次降价的百分率为 x，根据题意列方程得
A. 1681+x2=108B. 1681−x2=108
C. 1681−2x=108D. 168x21−x2=108

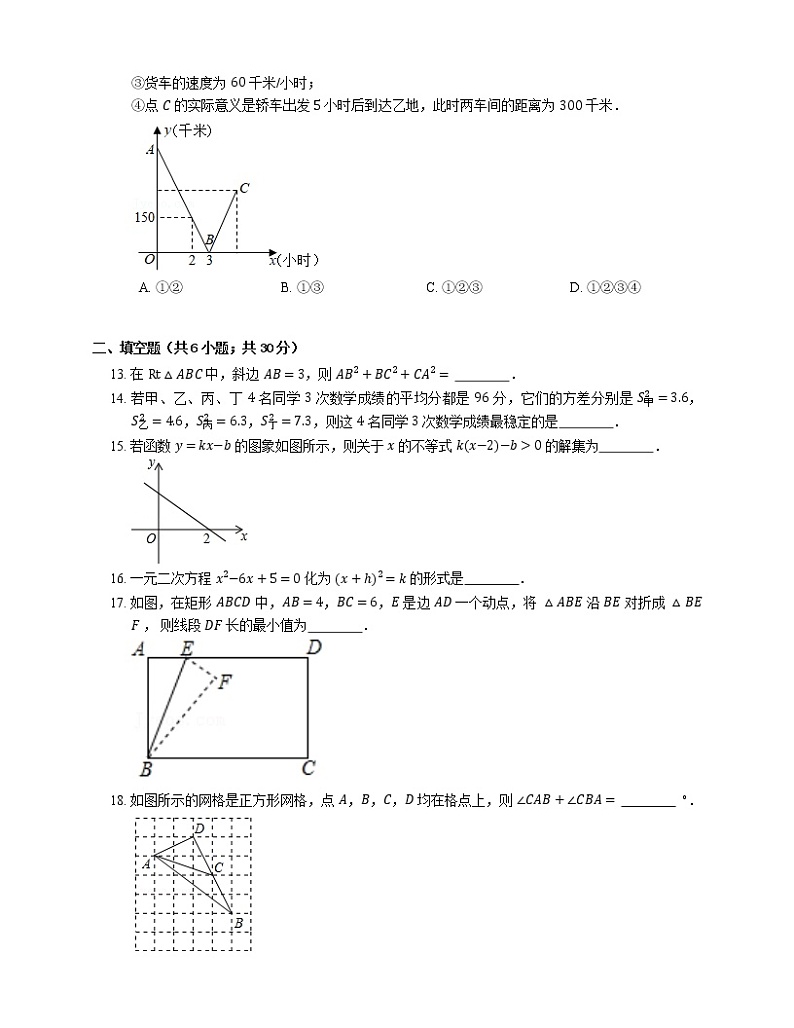
12. 一辆轿车和一辆货车分别从甲、乙两地同时出发，匀速相向而行，相遇后继续前行，已知两车相遇时轿车比货车多行驶了 90 千米，设行驶的时间为 x（小时），两车之间的距离为 y（千米），图中的折线表示从两车出发至轿车到达乙地这一过程中 y 与 x 之间的函数关系．根据图象提供的信息，下列说法正确的是
①甲乙两地的距离为 450 千米；
②轿车的速度为 90 千米/小时；
③货车的速度为 60 千米/小时；
④点 C 的实际意义是轿车出发 5 小时后到达乙地，此时两车间的距离为 300 千米．
A. ①②B. ①③C. ①②③D. ①②③④

二、填空题（共6小题；共30分）
13. 在 Rt△ABC 中，斜边 AB=3，则 AB2+BC2+CA2= ．

14. 若甲、乙、丙、丁 4 名同学 3 次数学成绩的平均分都是 96 分，它们的方差分别是 S甲2=3.6，S乙2=4.6，S丙2=6.3，S丁2=7.3，则这 4 名同学 3 次数学成绩最稳定的是 ．

15. 若函数 y=kx−b 的图象如图所示，则关于 x 的不等式 kx−2−b>0 的解集为 ．

16. 一元二次方程 x2−6x+5=0 化为 x+h2=k 的形式是 ．

17. 如图，在矩形 ABCD 中，AB=4，BC=6，E 是边 AD 一个动点，将 △ABE 沿 BE 对折成 △BEF ， 则线段 DF 长的最小值为 ．

18. 如图所示的网格是正方形网格，点 A，B，C，D 均在格点上，则 ∠CAB+∠CBA= ∘．

三、解答题（共6小题；共78分）
19. 解下列方程：
（1）x+32−16=0；
（2）2x2−3x−1=0．

20. 重庆一中开展了“爱生活•爱运动”的活动，以鼓励学生积极参与体育锻炼．为了解学生每周体育锻炼时间，学校在活动之前对八年级同学进行了抽样调查，并根据调查结果将学生每周的体育锻炼时间分为 3 小时、 4 小时、 5 小时、 6 小时、 7 小时共五种情况．小明根据调查结构制作了如图两幅统计图，请你结合图中所给信息解答下列问题：
【整理数据】
“爱生活•爱运动”的活动结束之后，再次抽查这部分学生的体育锻炼时间：
一周体育锻炼时间小时34567人数3515a10
活动之后部分学生体育锻炼时间的统计表
【分析数据】
平均数中位数众数活动之前锻炼时间小时555活动之后锻炼时间小时5.52bc
请根据调查信息分析：
（1）补全条形统计图，并计算 a= ，b= 小时，c= 小时；
（2）小亮同学在活动之前与活动之后的这两次调查中，体育锻炼时间均为 5 小时，根据体育锻炼时间由多到少进行排名统计，请问他在被调查同学中体育锻炼时间排名靠前的是 （填“活动之前”或“活动之后”），理由是 ；
（3）已知八年级共 2200 名学生，请估算全年级学生在活动结束后，每周体育锻炼时间至少有 6 小时的学生人数有多少人?

21. 在平面直角坐标系 xOy 中，一次函数的图象经过点 2,1，4,−2．
（1）求该一次函数的表达式；
（2）若点 A2m,y1，Bm+1,y2 在该一次函数的图象上，且 y1>y2，求实数 m 的取值范围．

22. 如图所示，点 E 在 △ABC 外部，点 D 在 BC 边上，DE 交 AC 于 F，若 ∠1=∠2=∠3，AD=AB，求证：AC=AE．

23. 某超市销售一款洗手液，这款洗手液成本价为每瓶 16 元，当销售单价定为每瓶 20 元时，每天可售出 60 瓶．市场调查反应：销售单价每上涨 1 元，则每天少售出 5 瓶．若设这款洗手液的销售单价上涨 x 元，每天的销售量利润为 y 元．
（1）每天的销售量为 瓶，每瓶洗手液的利润是 元；（用含 x 的代数式表示）
（2）若这款洗手液的日销售利润 y 达到 300 元，则销售单价应上涨多少元?

24. 如图，将一矩形纸片 OABC 放在平面直角坐标系内．O0,0，A6,0，C0,3，
（1）动点 Q 从 O 出发以每秒 1 个单位长度的速度沿 OC 向终点 C 运动，运动 23 秒时，动点 P 从点 A 出发以相同速度沿 AO 向终点 O 运动，当其中一个点到达终点时另一点也停止运动．设 P 点运动时间为 t 秒，
①求点 B 的坐标，并用 t 表示 OP 和 OQ；
②当 t=1 时，将 △OPQ 沿 PQ 翻折，O 恰好落在 CB 边上的 D 点处，求 D 点坐标；
（2）动点 Q 从 O 出发以每秒 1 个单位长度的速度沿 OC 向终点 C 运动，同时点 P 从点 A 出发以相同速度沿 AO 向终点 O 运动，是否存在这样的点 P 使 BP⊥PQ，若存在，请求出 PQ 的长度，若不存在，请说明理由．
答案
第一部分
1. D【解析】如图，
∵A3,0，B0,2，
∴OA=3，OB=2，
∴ 在直角 △AOB 中，由勾股定理得 AB=32+22=13．
又 ∵ 以点 A 为圆心，AB 为半径的弧交 x 轴负半轴于点 C，
∴AC=AB，
∴OC=AC−OA=13−3．
又 ∵ 点 C 在 x 轴的负半轴上，
∴C3−13,0．
2. B【解析】∵ 方程 k+3x2+5x+k2+2k−3=0，
∴k−3≠0，
∴k≠−3．
将 x=0 代入 k+3x2+5x+k2+2k−3=0，得：k2+2k−3=0，
解得：k1=−3（不合题意，舍去），k2=1．
3. C【解析】由表中数据知，这组数据的众数为 23.5 cm，所以影响店主决策的统计量是众数，故选C．
4. B【解析】根据题意得，Δ=b2−4ac=−2m−12−4m2=−4m+1≥0，
解得：m≤14，
故选：B．
5. B
【解析】A、因为 ∠A+∠B=∠C，∠A+∠B+∠C=180∘，
所以 ∠C=90∘，
所以 △ABC 为直角三角形，故此选项不合题意；
B、设 ∠A=3x∘，∠B=4x∘，∠C=5x∘，
3x+4x+5x=180，
解得：x=15，
则 5x∘=75∘，
所以 △ABC 不是直角三角形，故此选项符合题意；
C、因为 a2=c2−b2，
所以 a2+b2=c2，
所以 △ABC 为直角三角形，故此选项不合题意；
D、因为 a:b:c=3:4:5，
设 a=3x，b=4x，c=5x，
因为 3x2+4x2=5x2，
所以能构成直角三角形，故此选项不合题意．
6. C【解析】A. ∵AB∥CD，AD∥BC，
∴ 四边形 ABCD 是平行四边形，故此选项不符合题意；
B. ∵AB∥DC，
∴∠DAB+∠ADC=180∘，
∵∠DAB=∠DCB，
∴∠DCB+∠ADC=180∘，
∴AD∥BC，
∴ 四边形 ABCD 是平行四边形，故此选项不符合题意；
C. ∵AO=CO，AB=DC，∠AOB=∠COD，不能判定 △AOB≌△COD，
∴ 不能得到 ∠OAB=∠OCD，
∴ 不能得到 AB∥CD，
∴ 不能判定四边形 ABCD 是平行四边形，故此选项符合题意；
D. ∵AB∥DC，
∴∠OAB=∠OCD，
在 △AOB 和 △COD 中，
∠OAB=∠OCD∠AOB=∠CODBO=DO，
∴△AOB≌△CODAAS，
∴AB=DC，
又 ∵AB∥DC，
∴ 四边形 ABCD 是平行四边形，故此选项不符合题意．
7. B【解析】当 x=−2 时，y1=−1×−2−5=−3，
当 x=3 时，y2=−1×3−5=−8．
因为 −3>−8，
所以 y1>y2．
故选：B．
8. C【解析】∵ 点 A 的坐标为 1,3，
∴AB=1，OB=3，
∴OA=AB2+OB2=12+32=2，
∵ 将 Rt△AOB 沿直线 y=−x 翻折，得到 Rt△AʹOBʹ，
∴OBʹ=OB=3，AʹBʹ=AB=1，OAʹ=OA=2，
∴Aʹ−3,−1，
∵ 过 Aʹ 作 AʹC 垂直于 OAʹ 交 y 轴于点 C，
∴∠AʹOC+∠AʹCO=90∘，
∵∠AʹOBʹ+∠AʹOC=90∘，
∴∠AʹCO=∠AʹOBʹ，
∵∠AʹBʹO=∠OAʹC=90∘，
∴△AʹOBʹ∽△OCAʹ，
∴OCOAʹ=OAʹAʹBʹ，即 OC2=21，
∴OC=4，
∴C0,−4．
9. A【解析】连接 OA，如图所示：
∵ 四边形 ABCD 为菱形，点 O 是对角线 BD 的中点，
∴AD=AB=8，AO⊥BD，
∴∠ADB=∠CDB=12180∘−120∘=30∘，
在 Rt△AOD 中，OD=cs30∘⋅AD=32×8=43，
∵OE⊥CD，
∴∠DEO=90∘，
在 Rt△DOE 中，OE=12OD=12×43=23，
故选：A．
10. A
【解析】由题意知这组数据为 2，2，3，3，3，4，4，
所以样本容量为 7，中位数为 3，众数为 3，平均数为 2×2+3×3+2×47=3，
故选：A．
11. B【解析】设每次降价的百分率为 x，根据题意得：
1681−x2=108．
故选：B．
12. D【解析】由图象可知，甲乙两地的距离为 450 千米，故①说法正确；
设轿车和货车的速度分别为 V1 千米/小时，V2 千米/小时．
根据题意得 3V1+3V2=450 . 3V1−3V2=90．解得：V1=90，V2=60，
故轿车和货车速度分别为 90 千米/小时，60 千米/小时；故②③说法正确；
轿车到达乙地的时间为 450÷90=5（小时），
此时两车间的距离为 90+60×5−3=300（千米），故点 C 的实际意义是轿车出发 5 小时后到达乙地，此时两车间的距离为 300 千米．故④说法正确．
所以说法正确的是①②③④．
第二部分
13. 18
【解析】∵△ABC 为直角三角形，AB 为斜边，
∴AC2+BC2=AB2，又 AB=3，
∴AC2+BC2=AB2=9，
则 AB2+BC2+CA2=AB2+BC2+CA2=9+9=18．
14. 甲
【解析】∵S甲2=3.6，S乙2=4.6，S丙2=6.3，S丁2=7.3，
∴S甲2 ∴ 这 4 名同学 3 次数学成绩最稳定的是甲，
故答案为：甲．
15. x<4
【解析】∵ 一次函数 y=kx−b 的图象经过点 2,0，
∴2k−b=0，b=2k．
∵ 函数值 y 随 x 的增大而减小，
∴k<0；
∴ 关于 x 的不等式 kx−2−b>0 可化为 kx−2−2k>0，
移项得：kx>2k+2k，
即 kx>4k，
两边同时除以 k 得：x<4．
16. x−32=4
【解析】移项，得 x2−6x=−5，
配方得，x2−6x+9=−5+9，
x−32=4．
故答案为：x−32=4．
17. 213−4
【解析】如图，连接 DF，BD，
由图可知，DF>BD−BF，
当点 F 落在 BD 上时，DF 取得最小值，且最小值为 BD−BF 的长，
∵ 四边形 ABCD 是矩形，
∴AB=CD=4，BC=6，
∴BD=BC2+CD2=62+42=213，
由折叠性质知 AB=BF=4，
∴ 线段 DF 长度的最小值为 BD−BF=213−4，
故答案为：213−4．
18. 45
【解析】由图可知：AD=CD=12+22=5，AC=12+32=10，
∴∠ADC=90∘，
∴∠ACD=45∘，
∴∠BAC+∠BCA=∠ACD=45∘，
故答案为：45．
第三部分
19. （1）
x+32−16=0,∴x+32=16,∴x+3=±4,∴x1=1,x2=−7.
（2）
2x2−3x−1=0,∴a=2,b=−3,c=−1,
则
Δ=−32−4×2×−1=17>0,∴x=3±174,
即
x1=3+174,x2=3−174.
20. （1） 17；6；6
【解析】调查的总人数为：14÷28%=50（人），a=50−3−5−10−15=17（人），
活动结束后，再抽查，体育锻炼时间最多的是 6 小时，有 17 人，因此众数是 6 小时，把体育锻炼时间从小到大排列后处在第 25 位、 26 位的两个数都是 6 小时，因此中位数是 6．
（2） 活动之前；活动之前小亮的体育锻炼时间并列排名 19 名，而活动之后则并列排名 28 名
【解析】活动之前，体育锻炼为 6 小时的有：50−6−12−14−6=12 人，
小亮 5 小时锻炼时间的并列排名为：12+6+1=19 名，
而活动之后，小亮 5 小时锻炼时间的并列排名为：17+10+1=28 名．
（3） 2200×17+1050=1188（人），
答：八年级 2200 名学生中，生在活动结束后，每周体育锻炼时间至少有 6 小时的学生大约有 1188 人．
21. （1） 设一次函数的表达式为 y=kx+bk≠0，
把 2,1，4,−2 代入得
1=2k+b,−2=4k+b.
解得
k=−32,b=4.∴
一次函数的表达式为 y=−32x+4．
（2） ∵k=−32<0，
∴y 随 x 的增大而减少，
∵y1>y2
∴x1 ∴m<1．
22. 如图所示：
∵∠BAC=∠1+∠DAC，
∠DAE=∠2+∠DAC，
∴∠BAC=∠DAE，
又 ∵∠2+∠AFE+∠E=180∘，
∠3+∠DFC+∠C=180∘
∠2=∠3，∠AFE=∠DFC，
∴∠E=∠C，
在 △ABC 和 △ADE 中，
∠ABC=∠DAE,∠E=∠C,AB=AD,
∴△ABC≌△ADEAAS，
∴AC=AE．
23. （1） 60−5x；4+x
【解析】设这款洗手液的销售单价上涨 x 元，则每天的销售量为 60−5x 瓶，每瓶洗手液的利润为 20+x−16=4+x 元．
（2） 依题意得：
4+x60−5x=300,
整理得：
x2−8x+12=0,
解得：
x1=2,x2=6.
答：销售单价应上涨 2 元或 6 元．
24. （1） ① ∵O0,0，A6,0，C0,3，
∴OA=6，OC=3，
∵ 四边形 OABC 是矩形，
∴AB=OC=3，BC=OA=6，
∴B6,3，
∵ 动点 Q 从 O 点以每秒 1 个单位长的速度沿 OC 向终点 C 运动，运动 23 秒时，动点 P 从点 A 出发以相等的速度沿 AO 向终点 O 运动．
∴ 当点 P 的运动时间为 t（秒）时，
AP=t，OQ=23+t，
则 OP=OA−AP=6−t；
②当 t=1 时，OQ=53，则 CQ=CQ=OC−OQ=43，
由折叠可知：△OPQ△≌DPQ，
∴OQ=DQ=53，
由勾股定理，得：CD=1，
∴D1,3．
（2） 存在，如图所示，
设 P 点运动时间为 t 秒，则 OQ=AP=t，PO=6−t，
当 BP⊥PQ 时，∠BPQ=90∘，
∵ 四边形 OABC 是矩形，
∴∠COA=∠BAO=90∘，
∴∠OPQ=∠ABP，
∴△POQ≌△BAPAAS
∴PO=BA=3，即 6−t=3，
解得：t=3，
∴OQ=3，
∴PQ=OQ2+PO2=32，
∴ 存在点 P 使 BP⊥PQ，PQ=32．