优化提升专题训练（新高考） 导数的综合运用（含答案解析）学案

    导数的综合运用

【知识框图】

【自主热身，归纳总结】

1、（2020届山东师范大学附中高三月考）已知在区间上有极值点，实数a的取值范围是（    ）

A． B． C． D．

【答案】C

【解析】,由于函数在上有极值点，所以在上有零点.所以，解得.

故选：D.

2、【2019年高考浙江】已知，函数．若函数恰有3个零点，则

A．a<–1，b<0   B．a<–1，b>0   

C．a>–1，b<0   D．a>–1，b>0

【答案】C

【解析】当x＜0时，y＝f（x）﹣ax﹣b＝x﹣ax﹣b＝（1﹣a）x﹣b＝0，得x，

则y＝f（x）﹣ax﹣b最多有一个零点；

当x≥0时，y＝f（x）﹣ax﹣bx3（a+1）x2+ax﹣ax﹣bx3（a+1）x2﹣b，

，

当a+1≤0，即a≤﹣1时，y′≥0，y＝f（x）﹣ax﹣b在[0，+∞）上单调递增，

则y＝f（x）﹣ax﹣b最多有一个零点，不合题意；

当a+1＞0，即a>﹣1时，令y′＞0得x∈(a+1，+∞），此时函数单调递增，

令y′＜0得x∈[0，a+1），此时函数单调递减，则函数最多有2个零点.

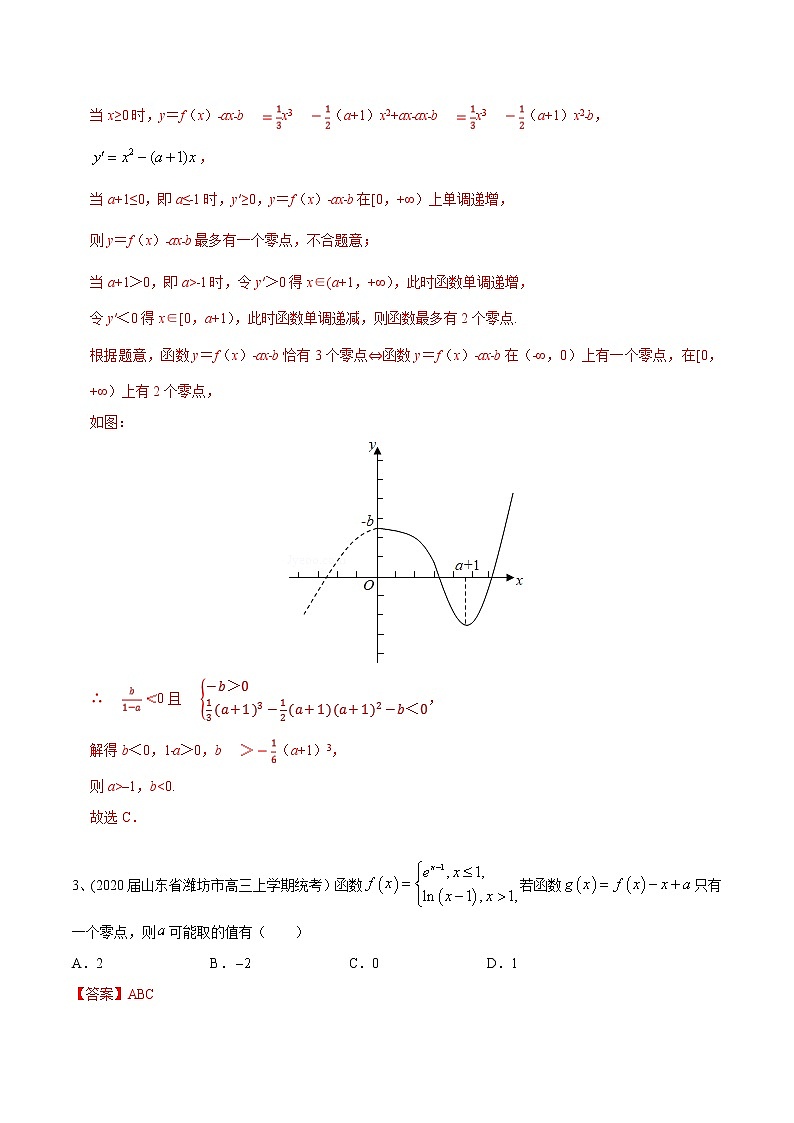
根据题意，函数y＝f（x）﹣ax﹣b恰有3个零点⇔函数y＝f（x）﹣ax﹣b在（﹣∞，0）上有一个零点，在[0，+∞）上有2个零点，

如图：

∴0且，

解得b＜0，1﹣a＞0，b（a+1）3，

则a>–1，b<0.

故选C．

3、(2020届山东省潍坊市高三上学期统考）函数若函数只有一个零点，则可能取的值有（    ）

A．2 B． C．0 D．1

【答案】ABC

【解析】∵只有一个零点，
∴函数与函数有一个交点，
作函数函数与函数的图象如下，

 
结合图象可知，当时；函数与函数有一个交点；
当时，，可得，令可得，所以函数在时，直线与相切，可得.

综合得：或.
故选：ABC.

4、（2020届山东省滨州市三校高三上学期联考）已知函数（e为自然对数的底），若且有四个零点，则实数m的取值可以为（    ）

A．1 B．e C．2e D．3e

【答案】CD

【解析】因为，可得，即为偶函数，

由题意可得时，有两个零点，

当时，，

即时，，

由，可得，

由相切，设切点为，

的导数为，可得切线的斜率为，

可得切线的方程为，

由切线经过点，可得，

解得：或（舍去），即有切线的斜率为，

故，

故选：CD.

5、（2020届山东省临沂市高三上期末）已知函数的定义域为，则（    ）

A．为奇函数

B．在上单调递增

C．恰有4个极大值点

D．有且仅有4个极值点

【答案】BD

【解析】因为的定义域为，所以是非奇非偶函数，

，

当时，，则在上单调递增.

显然，令，得，

分别作出，在区间上的图象，

由图可知，这两个函数的图象在区间上共有4个公共点，且两图象在这些公共点上都不相切，故在区间上的极值点的个数为4，且只有2个极大值点.

故选：BD.

6、【2019年高考北京理数】设函数（a为常数）．若f（x）为奇函数，则a=________；若f（x）是R上的增函数，则a的取值范围是___________．

【答案】

【解析】首先由奇函数的定义得到关于的恒等式，据此可得的值，然后利用可得a的取值范围.

若函数为奇函数，则即，

即对任意的恒成立，

则，得.

若函数是R上的增函数，则在R上恒成立，

即在R上恒成立，

又，则，

即实数的取值范围是.

7、（2020届山东省德州市高三上期末）已知函数（为常数）.

（1）若在处的切线与直线垂直，求的值；

（2）若，讨论函数的单调性；

【解析】（1）由题意，，则，

由于函数的图象在处的切线与直线垂直，

则，所以，因此，；

（2），则.

①若时，，

当或时，，时，，

所以在和单调递增，在单调递减，

②若时，，对，恒成立，在单调递增；

③若时，，

当或时，，时，，

所以在和单调递增，在单调递减；

【问题探究，变式训练】

题型一、函数单调性的讨论

知识点拨：利用导数研究函数的单调性主要是通过多函数求导，研究导函数的正负的问题，对于单调性的讨论问题时导数中经常考查的问题，讨论时要注意讨论的依据和标准，做到不重复不遗漏。

例1、【2020年高考全国Ⅰ卷理数】已知函数.

（1）当a=1时，讨论f（x）的单调性；

（2）当x≥0时，f（x）≥x3+1，求a的取值范围.

【解析】（1）当a=1时，f（x）=ex+x2–x，则=ex+2x–1．

故当x∈（–∞，0）时，<0；当x∈（0，+∞）时，>0．所以f（x）在（–∞，0）单调递减，在（0，+∞）单调递增．

（2）等价于.

设函数，则

.

（i）若2a+1≤0，即，则当x∈（0，2）时，>0.所以g（x）在（0，2）单调递增，而g（0）=1，故当x∈（0，2）时，g（x）>1，不合题意.

（ii）若0<2a+1<2，即，则当x∈(0，2a+1)∪(2，+∞)时，g'(x)<0；当x∈(2a+1，2)时，g'(x)>0.所以g(x)在(0，2a+1)，(2，+∞)单调递减，在(2a+1，2)单调递增.由于g(0)=1，所以g(x)≤1当且仅当g(2)=(7−4a)e−2≤1，即a≥.

所以当时，g(x)≤1.

（iii）若2a+1≥2，即，则g(x)≤.

由于，故由（ii）可得≤1.

故当时，g(x)≤1.

综上，a的取值范围是.

变式1、【2019年高考全国Ⅲ卷理数】已知函数.

（1）讨论的单调性；

（2）是否存在，使得在区间的最小值为且最大值为1？若存在，求出的所有值；若不存在，说明理由.

【答案】（1）见解析；（2）或.

【解析】（1）．

令，得x=0或.

若a>0，则当时，；当时，．故在单调递增，在单调递减；

若a=0，在单调递增；

若a<0，则当时，；当时，．故在单调递增，在单调递减.

（2）满足题设条件的a，b存在.

（i）当a≤0时，由（1）知，在[0，1]单调递增，所以在区间[0，l]的最小值为，最大值为.此时a，b满足题设条件当且仅当，，即a=0，．

（ii）当a≥3时，由（1）知，在[0，1]单调递减，所以在区间[0，1]的最大值为，最小值为．此时a，b满足题设条件当且仅当，b=1，即a=4，b=1．

（iii）当0<a<3时，由（1）知，在[0，1]的最小值为，最大值为b或．

若，b=1，则，与0<a<3矛盾.

若，，则或或a=0，与0<a<3矛盾．

综上，当且仅当a=0，或a=4，b=1时，在[0，1]的最小值为-1，最大值为1．

变式2、【2018年高考全国Ⅰ卷理数】已知函数．

（1）讨论的单调性；

【解析】（1）的定义域为，.

（i）若，则，当且仅当，时，所以在单调递减.

（ii）若，令得，或.

当时，；

当时，.

所以在单调递减，在单调递增.

变式3、（2020届山东省临沂市高三上期末）已知函数，函数（）.

（1）讨论的单调性；

【解析】

（1）解：的定义域为，，

当，时，，则在上单调递增；

当，时，令，得，令，得，则在上单调递减，在上单调递增；

当，时，，则在上单调递减；

当，时，令，得，令，得，则在上单调递增，在上单调递减；

变式4、（2019·夏津第一中学高三月考）已知函数．

（1）当时，讨论的单调性；

【解析】（1）函数的定义域为.

，

因为，所以，

①当，即时，

由得或，由得，

所以在，上是增函数， 在上是减函数；

②当，即时，所以在上是增函数；

③当，即时，由得或，由得，所以在，.上是增函数，在.上是减函

综上可知：

当时在，上是单调递增，在上是单调递减；

当时，在.上是单调递增；

当时在，上是单调递增，在上是单调递减.

题型二、给定单调区间，研究参数问题

知识点拨：给定单调区间，研究参数问题要转化为恒成立的问题，特别要注意等号。

例2、（2020届山东省潍坊市高三上学期统考）已知函数.

若在上是单调递增函数，求的取值范围；

【解析】 在上是单调递增函数,

在上，恒成立，即：

设

，

当时， 在上为增函数，

当时， 在上为减函数，

， 即 .

变式1、（2020届山东省九校高三上学期联考）已知函数，

（1）求的极值；

（2）若时，与的单调性相同，求的取值范围；

【解析】（1）的定义域为，，

当时，；当时，，

所以在单调递减，在    单调递增.

所以有极小值，无极大值.

（2）由（1）知，在单调递增.

则在单调递增，即在恒成立，

即在恒成立，

令，；，

所以当时，；当时，，

所以在单调递增，在单调递减，

又时，，所以，

∴.

题型三、函数的零点与极值点的综合问题

知识点拨：1、 研究函数的零点的问题，需要解决函数的单调性以及零点的支撑点这两个问题，其难点在于零点的支撑点的确定．一般地，确定零点的支撑点可有以下几种方法：一是以极值点作为支撑点，这是最为容易的一类；二是采用放放缩的方法，将函数转化为基本初等函数来加以解决；三是采用“形式化”的方式，即将函数分为几个部分，来分别找到这几个部分的零点，且它们有相同的变量法则，则取这些零点中的最大的或最小的作为支撑点．本题所采用的是放缩的方法来找支撑点．

例3、（2020届山东师范大学附中高三月考）已知函数，是函数的极值点，以下几个结论中正确的是（    ）

A． B． C． D．

【答案】AC

【解析】函数,,

∵是函数的极值点，∴，即，
,
,

,即A选项正确,B选项不正确;
,即C正确,D不正确.
故答案为:AC.

变式1、（2020·山东省淄博实验中学高三上期末）关于函数，下列判断正确的是（    ）

A．是的极大值点

B．函数有且只有1个零点

C．存在正实数，使得成立

D．对任意两个正实数，，且，若，则.

【答案】BD

【解析】A.函数的 的定义域为（0，+∞），

函数的导数f′（x），∴（0，2）上，f′（x）＜0，函数单调递减，（2，+∞）上，f′（x）＞0，函数单调递增，

∴x＝2是f（x）的极小值点，即A错误；

B.y＝f（x）﹣xlnx﹣x，∴y′10，

函数在（0，+∞）上单调递减，且f（1）﹣1ln1﹣1=1>0，f（2）﹣2ln2﹣2= ln2﹣1<0，∴函数y＝f（x）﹣x有且只有1个零点，即B正确；

C.若f（x）＞kx，可得k，令g（x），则g′（x），

令h（x）＝﹣4+x﹣xlnx，则h′（x）＝﹣lnx，

∴在x∈（0，1）上，函数h（x）单调递增，x∈（1，+∞）上函数h（x）单调递减，

∴h（x）⩽h（1）＜0，∴g′（x）＜0，

∴g（x）在（0，+∞）上函数单调递减，函数无最小值，

∴不存在正实数k，使得f（x）＞kx恒成立，即C不正确；

D.令t∈（0，2），则2﹣t∈（0，2），2+t＞2，

令g（t）＝f（2+t）﹣f（2﹣t）ln（2+t）ln（2﹣t）ln，

则g′（t）0，

∴g（t）在（0，2）上单调递减，

则g（t）＜g（0）＝0，

令x1＝2﹣t，

由f（x1）＝f（x2），得x2＞2+t，

则x1+x2＞2﹣t+2+t＝4，

当x2≥4时，x1+x2＞4显然成立，

∴对任意两个正实数x1，x2，且x2＞x1，若f（x1）＝f（x2），则x1+x2＞4，故D正确

故正确的是BD，

故选：BD．

变式2、（2020届山东省泰安市高三上期末）已知函数是定义在R上的奇函数，当时，，则下列命题正确的是（    ）

A．当时，

B．函数有3个零点

C．的解集为

D．，都有

【答案】BCD

【解析】（1）当时，，则由题意得，

∵ 函数是奇函数，

∴ ，且时，，A错；

∴ ，

（2）当时，由得，

当时，由得，

∴ 函数有3个零点，B对；

（3）当时，由得，

当时，由得，

∴ 的解集为，C对；

（4）当时，由得，

由得，由得，

∴ 函数在上单调递减，在上单调递增，

∴函数在上有最小值，且，

又∵ 当时，时，函数在上只有一个零点，

∴当时，函数的值域为，

由奇函数的图象关于原点对称得函数在的值域为，

∴ 对，都有，D对；

故选：BCD．

变式3、（2020届山东省枣庄市高三上学期统考）关于函数，下列判断正确的是（    ）

A．是的极大值点

B．函数有且只有1个零点

C．存在正实数，使得恒成立

D．对任意两个正实数，，且，若，则

【答案】BD

【解析】（1）的定义域为，，所以在上递减，在上递增，所以是的极小值点.故A选项错误.

（2）构造函数，，所以在上递减.而，，.所以有且只有一个零点.故B选项正确.

（3）构造函数.，由于，开口向下，和时，，即，时，故不存在正实数，使得恒成立，C选项错误.

（4）由（1）知，在上递减，在上递增， 是的极小值点.由于任意两个正实数，，且，，故.令，.由得，即，即，解得，则.所以.要证，即证，即证，由于，所以，故即证①.构造函数（先取），；，；.所以在上为增函数，所以，所以在上为增函数，所以.故当时，.即证得①成立，故D选项正确.

故选：BD.

变式4、【2020年高考全国Ⅲ卷理数】设函数，曲线在点(，f())处的切线与y轴垂直．

（1）求B．

（2）若有一个绝对值不大于1的零点，证明：所有零点的绝对值都不大于1．

【解析】（1）．

依题意得，即.

故．

（2）由（1）知，.

令，解得或.

与的情况为：

因为，所以当时，只有大于1的零点.

因为，所以当时，f（x）只有小于–1的零点．

由题设可知，

当时，只有两个零点和1.

当时，只有两个零点–1和.

当时，有三个等点x1，x2，x3，且，，．

综上，若有一个绝对值不大于1的零点，则所有零点的绝对值都不大于1.