2021年全国中考数学真题分类汇编--.图形与变换——平移与旋转

这是一份2021年全国中考数学真题分类汇编--.图形与变换——平移与旋转，共33页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

2021全国中考真题分类汇编（图形与变换）
----平移与旋转
一、选择题
1. （2021•湖北省武汉市）下列图形都是由一个圆和两个相等的半圆组合而成的，其中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
2. （2021•湖南省邵阳市）下列四个图形中，是中心对称图形的是（　　）
A． B．
C． D．
3. （2021•湖南省邵阳市）如图，在△AOB中，AO＝1，BO＝AB＝．将△AOB绕点O逆时针方向旋转90°，得到△A′OB′，连接AA′．则线段AA′的长为（　　）

A．1 B． C． D．
4. （2021•长沙市）下列几何图形中，是中心对称图形的是（ ）
A. B.
C. D.
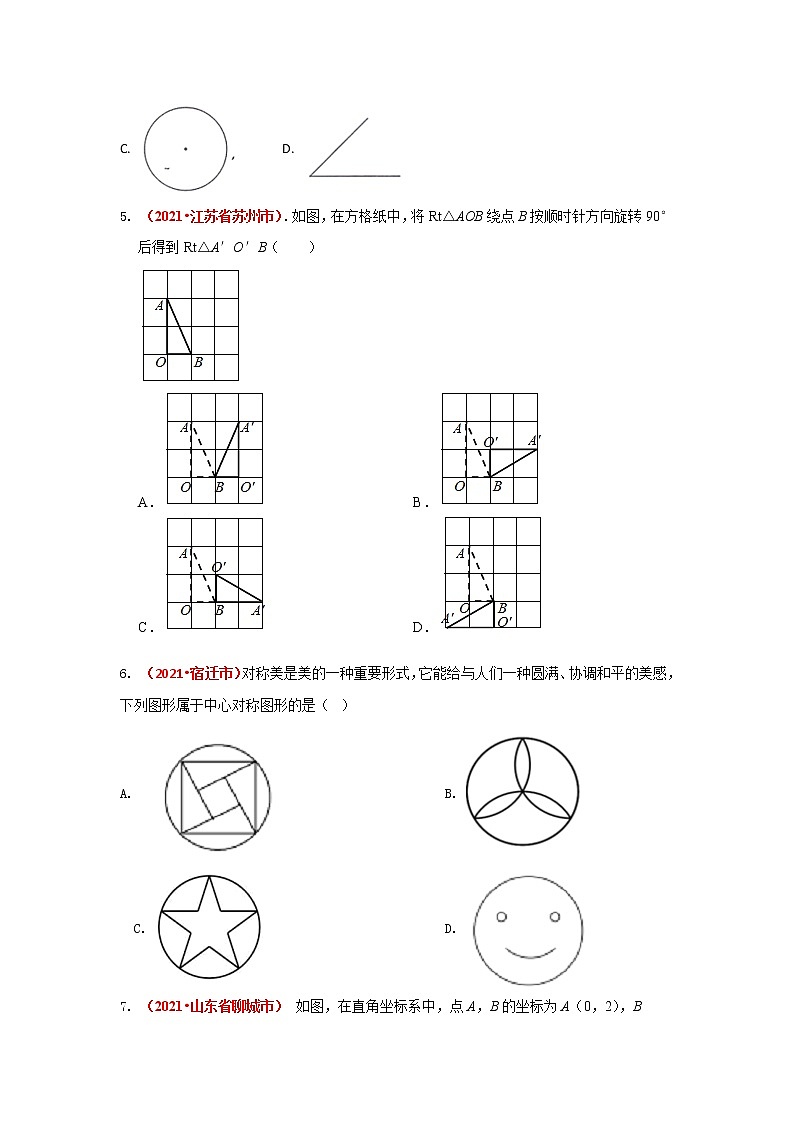
5. （2021•江苏省苏州市）．如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B（　　）

A． B．
C． D．

6. （2021•宿迁市）对称美是美的一种重要形式，它能给与人们一种圆满、协调和平的美感，下列图形属于中心对称图形的是（ ）
A. B.
C. D.
7. （2021•山东省聊城市） 如图，在直角坐标系中，点A，B的坐标为A（0，2），B（﹣1，0），将△ABO绕点O按顺时针旋转得到△A1B1O，若AB⊥OB1，则点A1的坐标为（ ）

A. （） B. （） C. （） D. （）
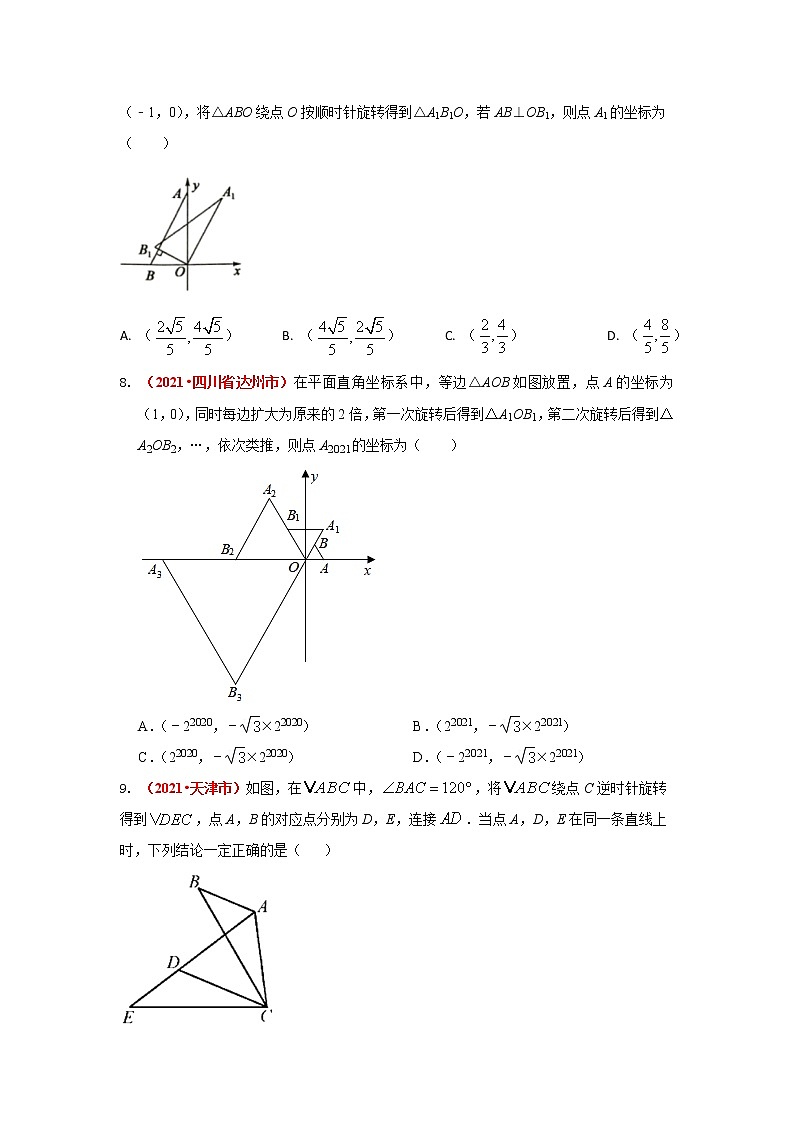
8. （2021•四川省达州市）在平面直角坐标系中，等边△AOB如图放置，点A的坐标为（1，0），同时每边扩大为原来的2倍，第一次旋转后得到△A1OB1，第二次旋转后得到△A2OB2，…，依次类推，则点A2021的坐标为（　　）

A．（﹣22020，﹣×22020） B．（22021，﹣×22021）
C．（22020，﹣×22020） D．（﹣22021，﹣×22021）
9. （2021•天津市）如图，在中，，将绕点C逆时针旋转得到，点A，B的对应点分别为D，E，连接．当点A，D，E在同一条直线上时，下列结论一定正确的是（ ）

A. B. C. D.
10. （2021•天津市）如图，的顶点A，B，C的坐标分别是，则顶点D的坐标是（ ）

A. B. C. D.
11. （2021•湖北省恩施州）下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
12. （2021•浙江省丽水市）四盏灯笼的位置如图．已知A，B，C，D的坐标分别是 (−1，b)，(1，b)，(2，b)，(3.5，b)，平移y轴右侧的一盏灯笼，使得y轴两侧的灯笼对称，则平移的方法可以是（ ）

A. 将B向左平移4.5个单位 B. 将C向左平移4个单位
C. 将D向左平移5.5个单位 D. 将C向左平移3.5个单位
13. （2021•湖北省荆门市）下列图形既是中心对称又是轴对称的是（　　）
A． B．
C． D．
14. 2021•湖南省永州市）如图，在平面内将五角星绕其中心旋转180°后所得到的图案是（　　）

A． B．
C． D．

15. （2021•黑龙江省大庆市）下列图形中，是中心对称图形但不是轴对称图形的是（ ）

16. （2021•江苏省无锡市）下列图形中，既是中心对称图形又是轴对称图形的是（　　）
A． B．
C． D．
17. （2021•齐齐哈尔市）下面四个图形中，既是轴对称图形也是中心对称图形的是（ ）
A. B.
C. D.
18. （2021•黑龙江省龙东地区）下列图形中，既是中心对称图形又是轴对称图形的是（ ）
A. B. C. D.

19. （2021•辽宁省本溪市）下列漂亮的图案中似乎包含了一些曲线，其实它们这种神韵是由多条线段呈现出来的，这些图案中既是中心对称图形又是轴对称图形的是（ ）
A. B.
C. D.

二．填空题
1. （2021•怀化市）如图，在平面直角坐标系中，已知A（﹣2，1），B（﹣1，4），C（﹣1，1），将△ABC先向右平移3个单位长度得到△A1B1C1，再绕C1顺时针方向旋转90°得到△A2B2C1，则A2的坐标是 　　．

2. （2021•江苏省苏州市）如图，射线OM，ON互相垂直，点B位于射线OM的上方，且在线段OA的垂直平分线l上，AB＝5．将线段AB绕点O按逆时针方向旋转得到对应线段A′B′，若点B′恰好落在射线ON上　 　．

3. （2021•山东省临沂市）在平面直角坐标系中，平行四边形ABCD的对称中心是坐标原点，顶点A、B的坐标分别是（﹣1，1）、（2，1），将平行四边形ABCD沿x轴向右平移3个单位长度，则顶点C的对应点C1的坐标是 　　．
4. （2021•湖北省随州市）如图，在中，，，，将绕点逆时针旋转角（）得到，并使点落在边上，则点所经过的路径长为______．（结果保留）


5. （2021•青海省）如图所示的图案由三个叶片组成，绕点O旋转120°后可以和自身重合．若每个叶片的面积为4cm2，∠AOB为120°，则图中阴影部分的面积之和为 　　cm2．

6. （2021•浙江省金华市）如图，菱形ABCD的边长为6cm，∠BAD＝60°，将该菱形沿AC方向平移2cm得到四边形A′B′C′D′，A′D′交CD于点E，则点E到AC的距离为 　　cm．

7. （2021•浙江省衢州卷）如图．将菱形ABCD绕点A逆时针旋转得到菱形，．当AC平分时，与满足的数量关系是（ ）

A. B.
C. D.
8.（2021•吉林省长春市）如图，在平面直角坐标系中，等腰直角三角形AOB的斜边OA在y轴上，，点B在第一象限.标记点B的位置后，将沿x轴正方向平移至的位置，使经过点B，再标记点的位置，继续平移至的位置，使经过点，此时点的坐标为 .

9. （2021•吉林省）如图，在平面直角坐标系中，点A的坐标为（0，3），点B的坐标为（4，0），连接AB，若将△ABO绕点B顺时针旋转90°，得到△A′BO′，则点A′的坐标为 　 　．



三、解答题
1.(2021·安徽省) 如图，在每个小正方形的边长为1个单位的网格中，的顶点均在格点（网格线的交点）上．
（1）将向右平移5个单位得到，画出；
（2）将（1）中的绕点C1逆时针旋转得到，画出．




2. （2021•株洲市） 将一物体（视为边长为米正方形）从地面上挪到货车车厢内．如图所示，刚开始点与斜面上的点重合，先将该物体绕点按逆时针方向旋转至正方形的位置，再将其沿方向平移至正方形的位置（此时点与点重合），最后将物体移到车厢平台面上．已知，，过点作于点，米，米．

（1）求线段的长度；
（2）求在此过程中点运动至点所经过的路程．



3. （2021•浙江省温州市）如图中4×4与6×6的方格都是由边长为1的小正方形组成．图1是绘成的七巧板图案，它由7个图形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）．
（1）选一个四边形画在图2中，使点P为它的一个顶点，并画出将它向右平移3个单位后所得的图形．
（2）选一个合适的三角形，将它的各边长扩大到原来的倍，画在图3中．





4. （2021•黑龙江省龙东地区）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，的三个顶点坐标分别为．

（1）画出关于x轴对称的，并写出点的坐标；
（2）画出绕点O顺时针旋转后得到的，并写出点的坐标；
（3）在（2）的条件下，求点A旋转到点所经过的路径长（结果保留）．





答案
一、选择题
1. （2021•湖北省武汉市）下列图形都是由一个圆和两个相等的半圆组合而成的，其中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
【分析】根据把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：A．既是轴对称图形又是中心对称图形；
B．不是轴对称图形，故此选项不合题意；
C．不是轴对称图形，故此选项不合题意；
D．是轴对称图形，故此选项不合题意；
故选：A．
2. （2021•湖南省邵阳市）下列四个图形中，是中心对称图形的是（　　）
A． B．
C． D．
【分析】根据中心对称图形的概念对各选项分析判断即可得解．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．
【解答】解：A．不是中心对称图形，故本选项不合题意；
B．不是中心对称图形，故本选项不合题意；
C．是中心对称图形，故本选项符合题意；
D．不是中心对称图形，故本选项不合题意．
故选：C．

3. （2021•湖南省邵阳市）如图，在△AOB中，AO＝1，BO＝AB＝．将△AOB绕点O逆时针方向旋转90°，得到△A′OB′，连接AA′．则线段AA′的长为（　　）

A．1 B． C． D．
【分析】由旋转性质可判定△AOA'为等腰直角三角形，再由勾股定理可求得AA'的长．
【解答】解：由旋转性质可知，OA＝OA'＝1，∠AOA'＝90°，
则△AOA'为等腰直角三角形，
∴AA'＝＝＝．
故选：B．

4. （2021•长沙市）下列几何图形中，是中心对称图形的是（ ）
A. B.
C. D.
【答案】C

5. （2021•江苏省苏州市）．如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B（　　）

A． B．
C． D．
【分析】本题主要考查旋转的性质，旋转过程中图形和大小都不发生变化，根据旋转性质判断即可．
【解答】解：A选项是原图形的对称图形故不正确；
B选项是Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，故B正确；
C选项旋转后的形状发生了改变，故C不正确；
D选项是按逆时针方向旋转90°，故D不正确；
故选：B．

6. （2021•宿迁市）对称美是美的一种重要形式，它能给与人们一种圆满、协调和平的美感，下列图形属于中心对称图形的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】根据中心对称图形的定义即可作出判断．
【详解】解：A、是中心对称图形，故选项正确；
B、不是中心对称图形，故选项错误；
C、不是中心对称图形，故选项错误；
D、不是中心对称图形，故选项错误．
故选：A．

7. （2021•山东省聊城市） 如图，在直角坐标系中，点A，B的坐标为A（0，2），B（﹣1，0），将△ABO绕点O按顺时针旋转得到△A1B1O，若AB⊥OB1，则点A1的坐标为（ ）

A. （） B. （） C. （） D. （）
【答案】A
【解析】
【分析】先求出AB，OA1，再作辅助线构造相似三角形，如图所示，得到对应边成比例，求出OC和A1C，即可求解．
【详解】解:如图所示，∵点A，B的坐标分别为A（0，2），B（﹣1，0），
∴OB=1，OA=2，
∴，
∵∠AOB=90°，
∴∠A1OB1=90°，
∴O A1⊥OB1，
又∵AB⊥OB1，
∴O A1∥AB，
∴∠1=∠2，
过A1点作A1C⊥x轴，
∴∠A1CO=∠AOB，
∴，
∴，
∵O A1=OA=2，
∴，
∴，，
∴，
故选：A．


8. （2021•四川省达州市）在平面直角坐标系中，等边△AOB如图放置，点A的坐标为（1，0），同时每边扩大为原来的2倍，第一次旋转后得到△A1OB1，第二次旋转后得到△A2OB2，…，依次类推，则点A2021的坐标为（　　）

A．（﹣22020，﹣×22020） B．（22021，﹣×22021）
C．（22020，﹣×22020） D．（﹣22021，﹣×22021）
【分析】每旋转6次，A的对应点又回到x轴正半轴，故A2021在第四象限，且OA2021＝22021，画出示意图，即可得到答案．
【解答】解：由已知可得：
第一次旋转后，A1在第一象限，OA1＝4，
第二次旋转后，A2在第二象限，OA2＝22，
第三次旋转后，A3在x轴负半轴，OA5＝23，
第四次旋转后，A6在第三象限，OA4＝22，
第五次旋转后，A5在第四象限，OA5＝35，
第六次旋转后，A6在x轴正半轴，OA6＝26，
.....．
如此循环，每旋转7次，而2021＝6×336+5，
∴A2021在第四象限，且OA2021＝42021，示意图如下：

OH＝OA2021＝52020，A2021H＝OH＝2020，
∴A2021（（42020，﹣×22020），
故选：C．

9. （2021•天津市）如图，在中，，将绕点C逆时针旋转得到，点A，B的对应点分别为D，E，连接．当点A，D，E在同一条直线上时，下列结论一定正确的是（ ）

A. B. C. D.
【答案】D
【解析】
【分析】由旋转可知，即可求出，由于，则可判断，即A选项错误；由旋转可知，由于，即推出，即B选项错误；由三角形三边关系可知，即可推出，即C选项错误；由旋转可知，再由，即可证明为等边三角形，即推出．即可求出，即证明
，即D选项正确；
【详解】由旋转可知，
∵点A，D，E在同一条直线上，
∴，
∵，
∴，故A选项错误，不符合题意；
由旋转可知，
∵为钝角，
∴，
∴，故B选项错误，不符合题意；
∵，
∴，故C选项错误，不符合题意；
由旋转可知，
∵，
∴为等边三角形，
∴．
∴，
∴，故D选项正确，符合题意；
故选D．
10. （2021•天津市）如图，的顶点A，B，C的坐标分别是，则顶点D的坐标是（ ）

A. B. C. D.
【答案】C
【解析】
【分析】根据平行四边形性质以及点的平移性质计算即可．
【详解】解：∵四边形ABCD平行四边形，
点B的坐标为(-2，-2)，点C的坐标为(2，-2)，
∴点B到点C为水平向右移动4个单位长度，
∴A到D也应向右移动4个单位长度，
∵点A的坐标为(0，1)，
则点D的坐标为(4，1)，
故选:C．
11. （2021•湖北省恩施州）下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
【分析】根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．
【解答】解：A．是轴对称图形，不是中心对称图形，故本选项不合题意；
B．既是轴对称图形，又是中心对称图形，故本选项符合题意；
C．不是轴对称图形，是中心对称图形，故本选项不合题意；
D．不是轴对称图形，是中心对称图形，故本选项不合题意．
故选：B．

12. （2021•浙江省丽水市）四盏灯笼的位置如图．已知A，B，C，D的坐标分别是 (−1，b)，(1，b)，(2，b)，(3.5，b)，平移y轴右侧的一盏灯笼，使得y轴两侧的灯笼对称，则平移的方法可以是（ ）

A. 将B向左平移4.5个单位 B. 将C向左平移4个单位
C. 将D向左平移5.5个单位 D. 将C向左平移3.5个单位
【答案】C
【解析】
【分析】直接利用利用关于y轴对称点的性质得出答案．
【详解】解：∵点A (−1，b) 关于y轴对称点为B (1，b)，
C (2，b)关于y轴对称点为(-2，b)，
需要将点D (3.5，b) 向左平移3.5+2=5.5个单位，
故选：C．

13. （2021•湖北省荆门市）下列图形既是中心对称又是轴对称的是（　　）
A． B．
C． D．
【分析】根据轴对称图形与中心对称图形的概念求解．
【解答】解：A、是轴对称图形，不是中心对称图形．故本选项不合题意；
B．不是轴对称图形，是中心对称图形．故本选项不合题意；
C．是轴对称图形，也是中心对称图形．故本选项符合题意；
D．是轴对称图形，不是中心对称图形．故本选项不合题意．
故选：C．

14. 2021•湖南省永州市）如图，在平面内将五角星绕其中心旋转180°后所得到的图案是（　　）C

A． B．
C． D．

15. （2021•黑龙江省大庆市）下列图形中，是中心对称图形但不是轴对称图形的是（ ）B

16.（2021•江苏省无锡市）下列图形中，既是中心对称图形又是轴对称图形的是（　　）A
A． B．
C． D．
【分析】根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解．
【解答】解：A．既是轴对称图形，又是中心对称图形，故本选项符合题意；
B．是轴对称图形，不是中心对称图形，故本选项不合题意；
C．不是轴对称图形，是中心对称图形，故本选项不合题意；
D．是轴对称图形，不是中心对称图形，故本选项不合题意．
故选：A．

17. （2021•齐齐哈尔市）下面四个图形中，既是轴对称图形也是中心对称图形的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】根据轴对称图形和中心对称图形的定义，逐一判断选项，即可．
【详解】解：A．既不是轴对称图形也不是中心对称图形，
B．是轴对称图形但不是中心对称图形，
C．既不是轴对称图形也不是中心对称图形，
D．既是轴对称图形也是中心对称图形．
故选D．

18. （2021•黑龙江省龙东地区）下列图形中，既是中心对称图形又是轴对称图形的是（ ）
A. B. C. D.

【答案】D
【解析】
【分析】根据轴对称图形及中心对称图形的概念可直接进行排除选项．
【详解】解：A、是轴对称图形但不是中心对称图形，故不符合题意；
B、是轴对称图形但不是中心对称图形，故不符合题意；
C、既是轴对称图形不是中心对称图形，故不符合题意；
D、是轴对称图形也是中心对称图形，故符合题意；
故选．
19. （2021•辽宁省本溪市）下列漂亮的图案中似乎包含了一些曲线，其实它们这种神韵是由多条线段呈现出来的，这些图案中既是中心对称图形又是轴对称图形的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】根据中心对称图形及轴对称图形的概念即可解答．
【详解】选项A，是中心对称图形，也是轴对称图形，符合题意；
选项B，不是中心对称图形，是轴对称图形，不符合题意；
选项C，不是中心对称图形，是轴对称图形，不符合题意；
选项D，不是中心对称图形，是轴对称图形，不符合题意．
故选A．

二．填空题
1. （2021•怀化市）如图，在平面直角坐标系中，已知A（﹣2，1），B（﹣1，4），C（﹣1，1），将△ABC先向右平移3个单位长度得到△A1B1C1，再绕C1顺时针方向旋转90°得到△A2B2C1，则A2的坐标是 　（2,2）　．

【分析】根据题意，画出图形，可得结论．
【解答】解：如图，观察图象可知A2(2,2)．

故答案为：（2,2）．

2. （2021•江苏省苏州市）如图，射线OM，ON互相垂直，点B位于射线OM的上方，且在线段OA的垂直平分线l上，AB＝5．将线段AB绕点O按逆时针方向旋转得到对应线段A′B′，若点B′恰好落在射线ON上　 　．

【分析】设OA的垂直平分线与OA交于C,将线段AB绕点O按逆时针方向旋转得到对应线段A′B′，C随之旋转到C'，过A'作A'H⊥ON于H，过C'作C'D⊥ON于D，过A'作A'E⊥DC'于E，由OA＝8，AB＝5，BC是OA的垂直平分线，可得OB＝5，OC＝AC＝4，BC＝3，cos∠BOC＝＝,sin∠BOC＝＝,证明∠BOC＝∠B'C'D＝∠C'A'E,从而在Rt△B'C'D中求出C'D＝，在Rt△A'C'E中，求出C'E＝，得DE＝C'D+C'E＝，即可得到A'到ON的距离是．
【解答】解：设OA的垂直平分线与OA交于C,将线段AB绕点O按逆时针方向旋转得到对应线段A′B′，
过A'作A'H⊥ON于H，过C'作C'D⊥ON于D，如图：

∵OA＝8，AB＝5，
∴OB＝4，OC＝AC＝4，cos∠BOC＝＝＝,
∵线段AB绕点O按逆时针方向旋转得到对应线段A′B′，C随之旋转到C'，
∴B'C'＝BC＝3，A'C'＝AC＝4,
∵∠B'C'D＝∠B'C'O﹣∠DC'O＝90°﹣∠DC'O＝∠B'OC',
∴cos∠B'C'D＝,
Rt△B'C'D中，＝，即＝，
∴C'D＝，
∵AE∥ON,
∴∠B'OC'＝∠C'A'E,
∴sin∠C'AE＝sin∠B'OC'＝sin∠BOC＝,
Rt△A'C'E中，＝，即＝，
∴C'E＝，
∴DE＝C'D+C'E＝，
而A'H⊥ON，C'D⊥ON，
∴四边形A'EDH是矩形，
∴A'H＝DE,即A'到ON的距离是．
故答案为：．

3. ．（2021•山东省临沂市）在平面直角坐标系中，平行四边形ABCD的对称中心是坐标原点，顶点A、B的坐标分别是（﹣1，1）、（2，1），将平行四边形ABCD沿x轴向右平移3个单位长度，则顶点C的对应点C1的坐标是 　（4，﹣1）　．
【分析】由题意A,C关于原点对称，求出点C的坐标，再利用平移的性质求出点C1的坐标可得结论．
【解答】解：∵平行四边形ABCD的对称中心是坐标原点，
∴点A,点C关于原点对称，
∵A(﹣1,1),
∴C(1,﹣1),
∴将平行四边形ABCD沿x轴向右平移3个单位长度，则顶点C的对应点C1的坐标是(4,﹣1),
故答案为：（4，﹣1）．

4. （2021•湖北省随州市）如图，在中，，，，将绕点逆时针旋转角（）得到，并使点落在边上，则点所经过的路径长为______．（结果保留）


5. ）（2021•青海省）如图所示的图案由三个叶片组成，绕点O旋转120°后可以和自身重合．若每个叶片的面积为4cm2，∠AOB为120°，则图中阴影部分的面积之和为 　4　cm2．

【分析】由于∠AOB为120°，由三个叶片组成，绕点O旋转120°后可以和自身重合，所以图中阴影部分的面积之和等于三个叶片的面积和的三分之一．
【解答】解：∵三个叶片组成，绕点O旋转120°后可以和自身重合，
而∠AOB为120°，
∴图中阴影部分的面积之和＝（4+4+4）＝4（cm2）．
故答案为4．

6. （2021•浙江省金华市）如图，菱形ABCD的边长为6cm，∠BAD＝60°，将该菱形沿AC方向平移2cm得到四边形A′B′C′D′，A′D′交CD于点E，则点E到AC的距离为 　2　cm．

【分析】连接BD,过点E作EF⊥AC于点F,根据菱形的性质可以证明三角形ABD是等边三角形，根据平移的性质可得AD∥A′E,可得＝,＝,解得A′E＝4(cm),再利用30度角所对直角边等于斜边的一半即可求出结论。
【解答】解：如图，连接BD,过点E作EF⊥AC于点F,

∵四边形ABCD是菱形，
∴AD＝AB,BD⊥AC,
∵∠BAD＝60°，
∴三角形ABD是等边三角形，
∵菱形ABCD的边长为6cm,
∴AD＝AB＝BD＝6cm,
∴AG＝GC＝3(cm),
∴AC＝6(cm),
∵AA′＝2(cm),
∴A′C＝4(cm),
∵AD∥A′E,
∴＝,
∴＝,
∴A′E＝4(cm),
∵∠EA′F＝∠DAC＝DAB＝30°,
∴EF＝A′E＝2(cm)．
故答案为：2．

7. （2021•浙江省衢州卷）如图．将菱形ABCD绕点A逆时针旋转得到菱形，．当AC平分时，与满足的数量关系是（ ）

A. B.
C. D.
【答案】C

8. （2021•吉林省长春市）如图，在平面直角坐标系中，等腰直角三角形AOB的斜边OA在y轴上，，点B在第一象限.标记点B的位置后，将沿x轴正方向平移至的位置，使经过点B，再标记点的位置，继续平移至的位置，使经过点，此时点的坐标为 .


9. （2021•吉林省）如图，在平面直角坐标系中，点A的坐标为（0，3），点B的坐标为（4，0），连接AB，若将△ABO绕点B顺时针旋转90°，得到△A′BO′，则点A′的坐标为 　 　．



三、解答题
1.(2021·安徽省) 如图，在每个小正方形的边长为1个单位的网格中，的顶点均在格点（网格线的交点）上．
（1）将向右平移5个单位得到，画出；
（2）将（1）中的绕点C1逆时针旋转得到，画出．

【答案】（1）作图见解析；（2）作图见解析．
【解析】
【分析】（1）利用点平移的规律找出、、，然后描点即可；
（2）利用网格特点和旋转的性质画出点，即可．
【详解】解：（1）如下图所示，为所求；
（2）如下图所示，为所求；

2. （2021•株洲市） 将一物体（视为边长为米正方形）从地面上挪到货车车厢内．如图所示，刚开始点与斜面上的点重合，先将该物体绕点按逆时针方向旋转至正方形的位置，再将其沿方向平移至正方形的位置（此时点与点重合），最后将物体移到车厢平台面上．已知，，过点作于点，米，米．

（1）求线段的长度；
（2）求在此过程中点运动至点所经过的路程．
【答案】（1）米；（2）4米．

3. （2021•浙江省温州市）如图中4×4与6×6的方格都是由边长为1的小正方形组成．图1是绘成的七巧板图案，它由7个图形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）．
（1）选一个四边形画在图2中，使点P为它的一个顶点，并画出将它向右平移3个单位后所得的图形．
（2）选一个合适的三角形，将它的各边长扩大到原来的倍，画在图3中．

【分析】（1）直接将其中任意四边形向右平移3个单位得出符合题意的图形；
（2）直接将其中任意一三角形边长扩大为原来的倍，即可得出所求图形．
【解答】解：（1）如图2所示，即为所求；

（2）如图3所示，即为所求．


4. （2021•黑龙江省龙东地区）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，的三个顶点坐标分别为．

（1）画出关于x轴对称的，并写出点的坐标；
（2）画出绕点O顺时针旋转后得到的，并写出点的坐标；
（3）在（2）的条件下，求点A旋转到点所经过的路径长（结果保留）．
【答案】（1）见解析，；（2）见解析，；（3）
【解析】
【分析】（1）分别作出点A、B关于x轴的对称点，然后依次连接即可，最后通过图象可得点的坐标；
（2）根据旋转的性质分别作出点A、B绕点O旋转90°的点，然后依次连接，最后根据图象可得点的坐标；
（3）由（2）可先根据勾股定理求出OA的长，然后根据弧长计算公式进行求解．
【详解】解：（1）如图所示：

∴由图象可得；
（2）如图所示：

∴由图象可得；
（3）由（2）的图象可得：点A旋转到点所经过的路径为圆弧，
∵，
∴点A旋转到点所经过的路径长为．