





北师大版必修1第四章 函数应用2实际问题的函数建模2.3函数建模案例教学演示ppt课件
展开数学建模活动是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建数学模型解决问题的过程.主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、构建数学模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题.数学建模活动是基于数学思维运用模型解决实际问题的一类综合实践活动,是高中阶段数学课程的重要内容.
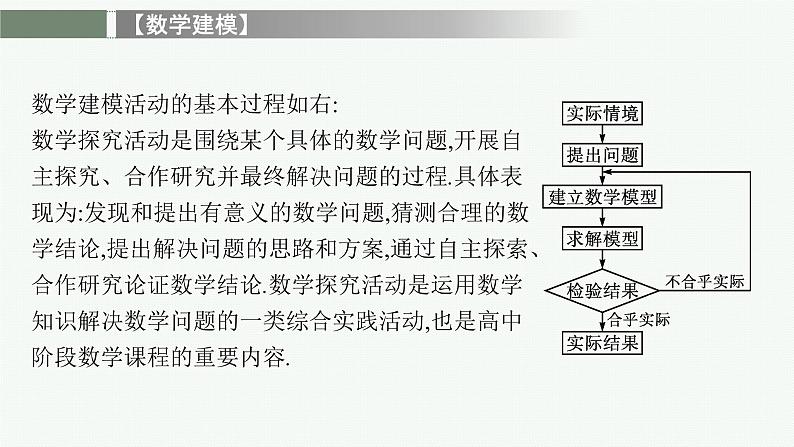
数学建模活动的基本过程如右:数学探究活动是围绕某个具体的数学问题,开展自主探究、合作研究并最终解决问题的过程.具体表现为:发现和提出有意义的数学问题,猜测合理的数学结论,提出解决问题的思路和方案,通过自主探索、合作研究论证数学结论.数学探究活动是运用数学知识解决数学问题的一类综合实践活动,也是高中阶段数学课程的重要内容.
本专题在必修课程和选择性必修课程的基础上,通过具体实例,建立一些基于数学表达的经济模型和社会模型,包括存款贷款模型、投入产出模型、经济增长模型、凯恩斯模型、生产函数模型、等级评价模型、人口增长模型、信度评价模型等.在教学活动中,要让学生知道这些模型形成的背景、数学表达的道理、模型参数的意义、模型适用的范围,提升数学建模、数学抽象、数学运算和直观想象素养;知道其中的有些模型(以及模型的衍生)获得诺贝尔经济学奖的理由,理解数学的应用,提高学习数学的兴趣,提升实践能力和创新能力.
实例1 跑道问题【情境】 400 m标准跑道的内圈如图所示,其中左右两边均是半径为36 m的半圆弧.(注:400 m标准跑道最内圈约为400 m)(1)求每条直道的长度(圆周率取3.14,结果精确到1 m);(2)建立平面直角坐标系xOy,写出跑道上半部分对应的函数解析式.
【分析】 在平面直角坐标系中,探索并掌握圆的标准方程与一般方程.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系.本题解答如下:(1)因为跑道两端的弧形合起来是一个完整的圆周,所以弧形部分跑道的长度为2×3.14×36=226.08(m),两条直道长度为400-226.08=173.92(m).所以每条直道长约为173.92÷2≈87(m).
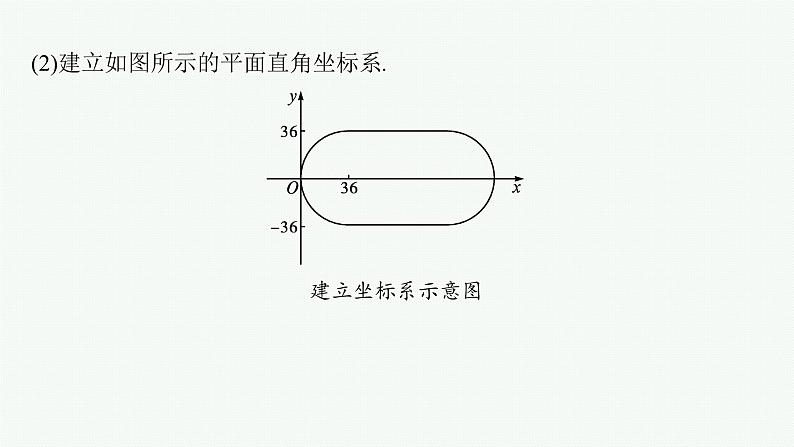
(2)建立如图所示的平面直角坐标系.
实例2 鞋子尺码问题【情境】 网上购鞋常常看到下面的表格.脚长与鞋号对应表
请解决下面的问题:(1)找出满足表中对应规律的计算公式,通过实际脚长a计算出鞋号b;(2)根据计算公式,计算30号童鞋所对应的脚长是多少?(3)如果一个篮球运动员的脚长为282 mm,根据计算公式,他该穿多大号的鞋?
【分析】 数学建模素养的一个基本表现,就是能够针对具体的数据,选择合适的数学模型表达数量之间的关系,解决实际问题.(1)可以把表中的两行数据看成两个数列,分别为{an}和{bn},仔细观察可以知道,这两个数列分别满足下面的递推关系:an+1=an+5,a1=220;bn+1=bn+1,b1=34.由此得到an=215+5n和bn=33+n,于是有bn=0.2an-10.进一步,将脚长和对应的鞋号记作(a,b),在平面直角坐标系中描点,观察到线性关系,然后建立关系式b=0.2a-10.
构建数据表,利用计算工具的电子表格作出散点图,选择几种函数模型进行拟合;对比拟合结果,发现线性函数的拟合效果最好,进而确定计算公式是一个线性模型,最后确定模型中的参数,如图所示.
(2)令b=30,代入公式b=0.2a-10,得a=200,脚的长度为200 mm.(3)当a=282时,代入公式b=0.2a-10,得b=46.4.分两种情况:如果简单地进行“四舍五入”,那么选46号鞋;如果想穿鞋不挤脚,可以选47号鞋.
【情境】 为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部门在该市随机调查了200户居民六月份的用电量(单位:kW·h),以了解这个城市家庭用电量的情况.数据如下:
根据以上数据,应当如何确定阶梯电价中的电量临界值,才能使得电价更为合理?【分析】 选取六月份调查,是因为这个城市六月份的部分时间需要使用空调,因此六月份的用电量在一年12个月中处于中等偏上水平.如果阶梯电价临界值的确定依赖于居民月用电量的分布,例如计划实施3阶的阶梯电价,有人给出一个分布如下:75%用户在第一档(最低一档),20%用户在第二档,5%用户在第三档(最高一档).这样,需要通过样本数据估计第一档与第二档、第二档与第三档的两个电量临界值,即75%和95%这两个电量临界值.
通过样本估计总体百分位数的要领是对样本数据进行排序,得到有序样本(在统计学中称之为顺序统计量).
利用电子表格软件,对上面的样本数据进行排序,可以得到下面的结果:
样本数据总共有200个,最小值是8,最大值是626,说明200户居民六月份的最小用电量为8 kW·h,最大用电量为626 kW·h,极差为618.初中统计内容中学过的中位数,相当于50%分位数.因为数据量是200,所以这组数据的样本中位数就是有序样本第100个数130和第101个数130的平均数,即130,说明这个城市六月份居民用电量的中间水平大约在130 kW·h.下面确定75%和95%这两个电量临界值.类似中位数的计算,因为200×75%= 150,所以第一个临界值为有序样本中第150个数178和第151个数178的平均数,仍然是178.因为200×95%=190,所以第二个临界值为有序样本中第190个数289和第191个数304的平均数,这个平均数为296.5(因为是对百分位数的估计,为了便于操作可以取值为297).
依据确定了的电量临界值,阶梯电价可以规定如下:用户每月用电量不超过178 kW·h(或每年用电量不超过2 136 kW·h),按第一档电价标准缴费;每月用电量(单位:kW·h)在区间(178,297]内(或每年用电量在区间(2 136,3 564]内),其中的178 kW·h按第一档电价标准缴费,超过178 kW·h的部分按第二档电价标准缴费;每月用电量超过297 kW·h(或每年用电量超过3 564 kW·h),其中的178 kW·h按第一档电价标准缴费,(297-178)=119 kW·h按第二档电价标准缴费,超过297 kW·h的部分按第三档电价标准缴费.社会上对这种制定阶梯电价的原则和方法存在不同意见,教师可以引导学生讨论制定合理阶梯电价的原则和方法.
高中数学1 数学建模实例教案配套课件ppt: 这是一份高中数学1 数学建模实例教案配套课件ppt,文件包含第七章再练一课范围§1~§3pptx、第七章再练一课范围§1~§3docx等2份课件配套教学资源,其中PPT共48页, 欢迎下载使用。
北师大版 (2019)选择性必修 第一册1 数学建模实例多媒体教学ppt课件: 这是一份北师大版 (2019)选择性必修 第一册1 数学建模实例多媒体教学ppt课件,文件包含第六章再练一课范围§1~§2pptx、第六章再练一课范围§1~§2docx等2份课件配套教学资源,其中PPT共33页, 欢迎下载使用。
高中数学北师大版 (2019)选择性必修 第一册1 数学建模实例课文ppt课件: 这是一份高中数学北师大版 (2019)选择性必修 第一册1 数学建模实例课文ppt课件,文件包含第五章再练一课范围§1~§3pptx、第五章再练一课范围§1~§3docx等2份课件配套教学资源,其中PPT共32页, 欢迎下载使用。













