2021学年19．7 直角三角形全等的判定教学演示课件ppt

这是一份2021学年19．7 直角三角形全等的判定教学演示课件ppt，共16页。PPT课件主要包含了“SAS”，“ASA”，“AAS”，“SSS”，“HL”等内容，欢迎下载使用。

在前面的学习中，我们已经掌握了判定一般三角形全等的方法，这些方法也可以用来判定特殊三角形（如直角三角形）的全等。 但是，特殊三角形（如直角三角形）具有其本身的特殊性质，在判定它们全等时，应考虑到这些特殊性。 本节，我们将学习判定直角三角形全等的一种特殊方法。
我们学习了哪些三角形全等的判定公理？
边角边公理（SAS）： 有两边和它们的夹角对应相等的两个三角形全等。
角边角公理（ASA）： 有两角和它们的夹边对应相等的两个三角形全等。
角角边公理（AAS）： 有两角和其中一角的对边对应相等的两个三角形全等。
边边边公理（SSS）： 有三边对应相等的两个三角形全等。
1、在两个直角三角形中，“边、边、角”对 应相等的情况有几种？
两个直角三角形中，如果“边、边、角”对应相等，那么其中对应相等的角一定是直角，因此对应相等的边只能分别是斜边和一条直角边，我们只要研究：斜边和一条直角边对应相等的两个直角三角形是否全等？
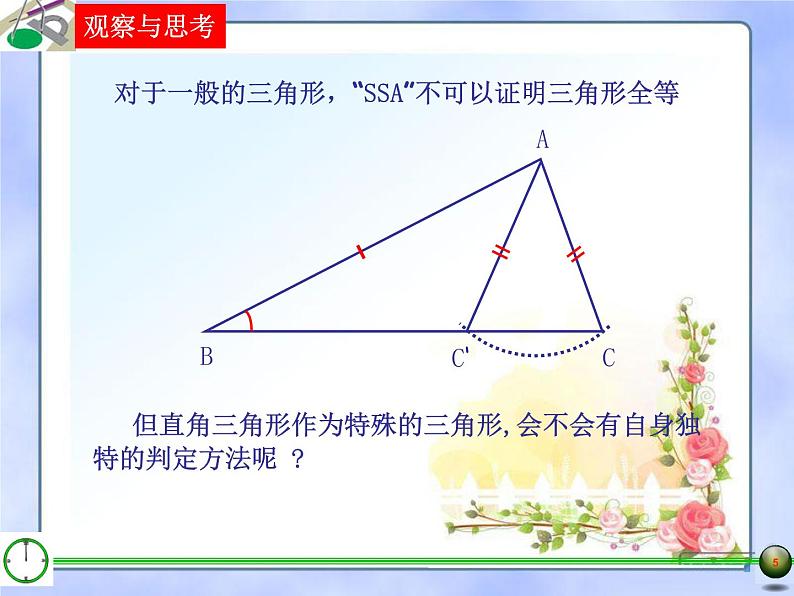
对于一般的三角形，“SSA”不可以证明三角形全等
但直角三角形作为特殊的三角形,会不会有自身独特的判定方法呢 ?
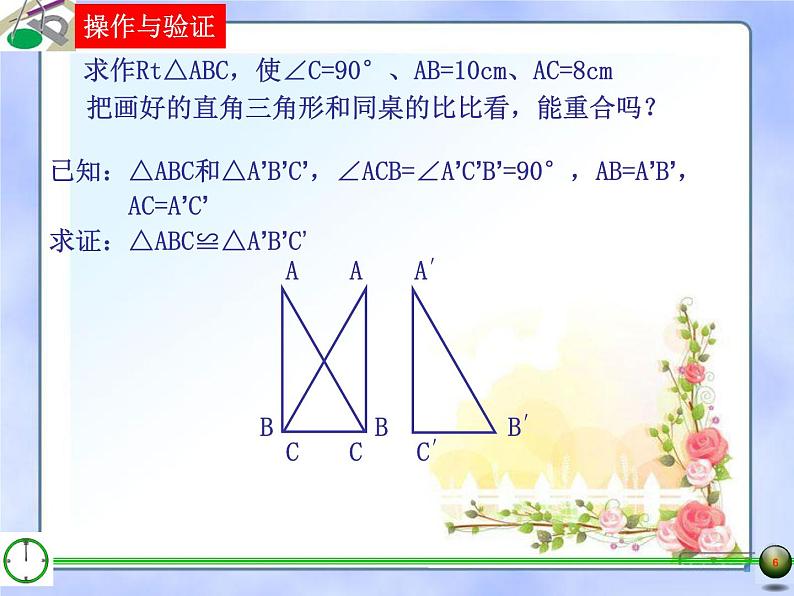
求作Rt△ABC，使∠C=90°、AB=10cm、AC=8cm
把画好的直角三角形和同桌的比比看，能重合吗？
已知：△ABC和△A’B’C’，∠ACB=∠A’C’B’=90°，AB=A’B’， AC=A’C’求证：△ABC≌△A’B’C’
直角三角形全等的判定定理
如果两个直角三角形的斜边和一条直角边对应相等，那么这两个直角三角形全等，（简记成“HL”.）
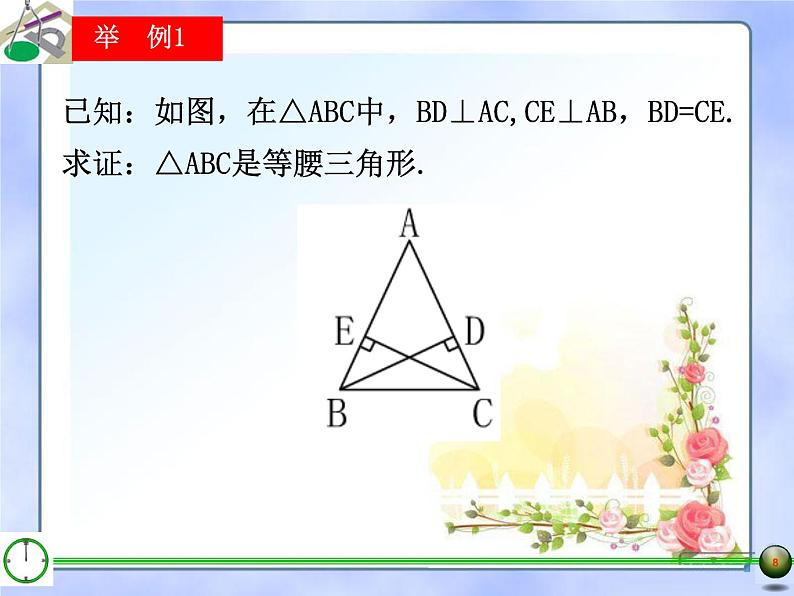
已知：如图，在△ABC中，BD⊥AC,CE⊥AB，BD=CE.
求证：△ABC是等腰三角形.
已知：如图，PD⊥OA，PE⊥OB，垂足分别是D，E， 且PD=PE . 求证：点P在∠AOB的角平分线上.
求证：在一个角的内部（包括顶点）且到角的两边距离相等的点，在这个角的平分线上
已知：在△ABC中，AD是∠BAC的平分线，且BD=CD， DE、DF分别垂直于AB、AC，垂足分别为点E、F.求证：EB=FC.
已知：如图，EC⊥AB，FD⊥AB，垂足分别为C、D， AF=BE，FD=EC.求证：AC=BD.
已知：如图，AB⊥BC，AE⊥ED，垂足分别为点B、E， AB=AE，∠1=∠2.求证：BC=ED
已知：如图，AD⊥CD，BC⊥CD，D、C分别为垂足， AB的垂直平分线EF交AB于点E，交CD于点F， BC=DF.求证：AD=FC
灵活运用各种方法证明直角三角形全等