2022届高考数学一轮复习专题必刷卷（8）空间向量与立体几何

这是一份2022届高考数学一轮复习专题必刷卷（8）空间向量与立体几何，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
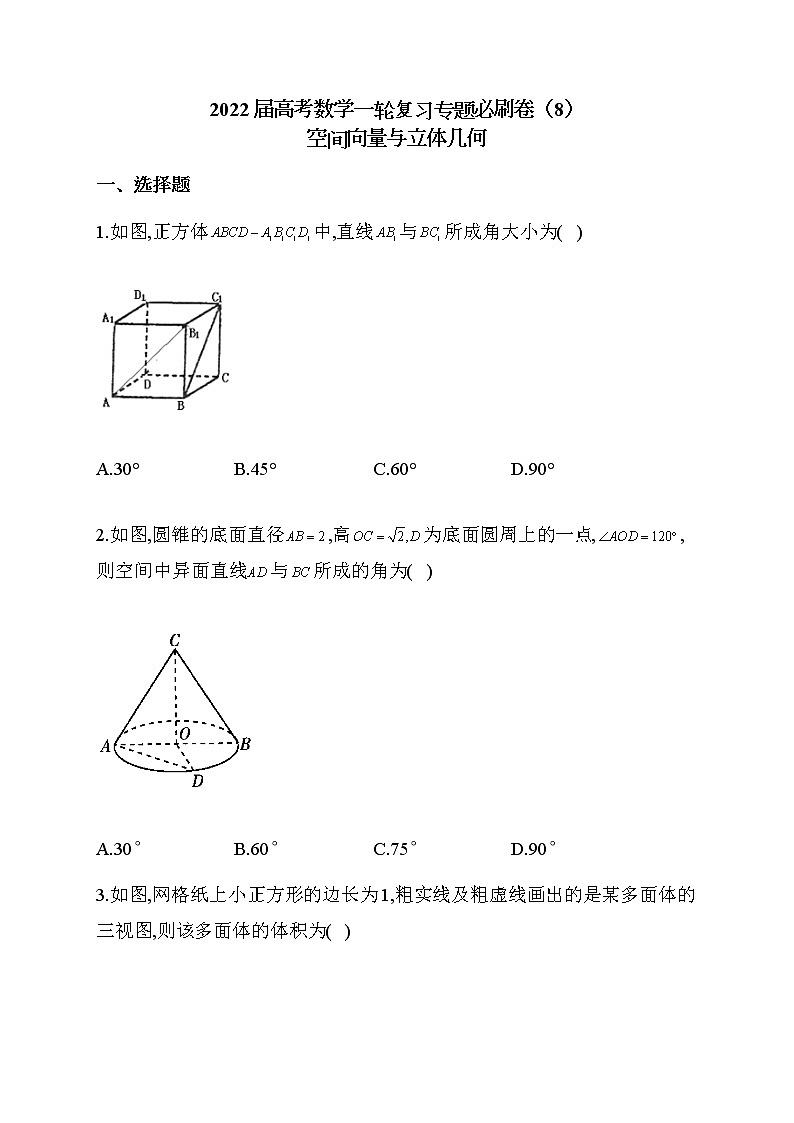
1.如图,正方体中,直线与所成角大小为( )
A.30°B.45°C.60°D.90°
2.如图,圆锥的底面直径,高为底面圆周上的一点,,则空间中异面直线与所成的角为( )
A.30°B.60°C.75°D.90°
3.如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )
A. B. C.1D.
4.已知一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积的比值为是( )
A.B.C.D.
5.已知是面积为的等边三角形，且其顶点都在球O的球面上，若球O的表面积为，则O到平面的距离为（ ）
A．B．C．1D．
6.在正方体中，点P在线段上运动，则异面直线CP与所成的角θ的取值范围是( )
A.B.C.D.
二、填空题
7.已知点P是棱长为2的正方体内部的一动点,且,则的值取最小时,与的夹角为_____________.
8.已知正方体的棱长为1,若动点在线段上运动,则的取值范围是____________________.
9.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的体积为________________.
三、解答题
10.如图，直三棱柱中，D、E分别是AB、的中点.
（1）证明：平面；
（2），，求三棱锥的体积.
参考答案
1.答案：C
解析：∵
∴是直线与所成角，
∵是等边三角形，
∴直线与所成角.
故选：C.
2.答案：B
解析：因为，,又,所以.因为,,所以,所以,所以异面直线与所成的角为60°.
3.答案：B
解析：由已知中的三视图可得该几何体是一个三棱锥，其直观图如下图所示：
故其体积，故选B．
4.答案：A
解析：设圆柱的底面半径为r,高为h,则,所以表面积与侧面积的比值为.
5.答案：C
解析：由等边三角形的面积为，得，得，则的外接圆半径.设球的半径为，则由球的表面积为，得，得，则球心到平面的距离，故选C.
6.答案：D
解析：连接，因为，所以CP与所成的角就是CP与所成的角，即.当点P从向A运动时，从0°增大到60°，但当点P与重合时，，与CP与为异面直线矛盾，所以异面直线CP与所成的角的取值范围是.
7.答案：90°
解析：由题意，取的中点M,则
.
因为,所以点P在以点A为球心,以2为半径，且位于正方体内部的球面上（包括球面与正方体的公共点），
所以,
因为，所以，
所以与的夹角为90°.
8.答案：
解析：依题意,设,其中,则,因此的取值范围是.
9.答案：
解析：如图,设球心为O,半径为r,则在中,,解得,则球O的体积.
10.答案：（1）证明：连结交于点F，则F为中点.又D是AB中点，
连结DF，则.因为平面，不包含于平面，
所以平面.
（2）解：因为是直三棱柱，所以.由已知，D为AB的中点，所以.又，于是平面.
由，得，，，，，故，即
所以三棱锥的体积为：.