

2018年数学中考第一轮复习讲义:2018年数学中考第一轮复习讲义:第9讲 几何初步
展开第九讲 几何初步
知识回顾
(一)、直线、射线、线段
1.直线的性质:(1)两条直线相交,只有 个交点;
(2)经过两点有且只有一条直线,即两点确定 条直线.
2.线段的性质:两点之间 最短.
3.线段的中点性质:若C是线段AB中点,则AC=BC= ;AB=2 =2 .
4.在同一平面内,两条直线只有两种位置关系: , .
5.垂线的性质:(1)经过一点有 条直线垂直于已知直线;(2)直线外一点与直线上各点连接的所有线段中, 最短.
6.点到直线的距离:从直线外一点向已知直线作垂线,这一点和垂足之间线段的长度叫做 .
(二)角
1.角平分线的性质:若OC是∠AOB的平分线,则∠AOC=∠ =∠ ,∠AOB=2∠ =2∠ .
2.余角和补角的性质:同角(或等角)的余角 ;同角(或等角)的补角 .
3.角度之间的转换关系:1°= ′,1′=60″,1°= ″.
4.对顶角的性质:对顶角 .
(三)三线八角
直线a,b被直线l所截,构成八个角(如图)
∠1和∠5,∠4和∠8,∠2和∠6,∠3和∠7是 ;∠2和∠8,∠3和∠5是 ;∠5和∠2,∠3和∠8是 .
(四)平行线的性质
1.平行线公理:
经过直线外一点有 条直线与已知直线平行.
2.平行线的基本性质:
(1)两直线平行, 相等;
(2)两直线平行, 相等;
(3)两直线平行, 互补
(五)平行线的判定方法
1. 相等,两直线平行;
2. 相等,两直线平行;
3. ,两直线平行;
4.传递性:如果a∥b,b∥c,那么
基础检测
1.(2017广东)已知∠A=70°,则∠A的补角为( )
A.110° B.70° C.30° D.20°
2.(2017浙江湖州)七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那副图是( )
A.B.C.D.
3.(2017•宁德)如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
A.BM=AB B.AM+BM=AB C.AM=BM D.AB=2AM
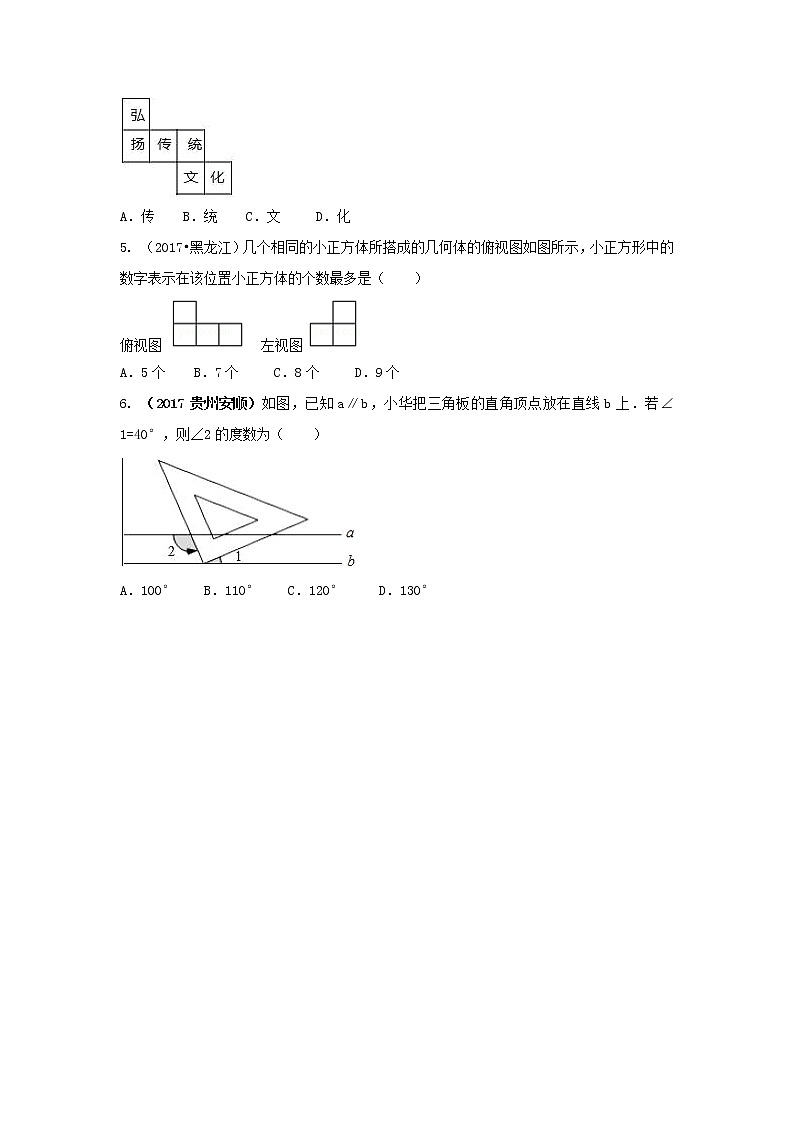
4. (2017湖北江汉)如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
A.传 B.统 C.文 D.化
5. (2017•黑龙江)几个相同的小正方体所搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置小正方体的个数最多是( )
俯视图 左视图
A.5个 B.7个 C.8个 D.9个
6. (2017贵州安顺)如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
考点解析
考点一、点和线
【例题】(2017湖北随州)某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.经过直线外一点,有且只有一条直线与这条直线平行
【考点】IC:线段的性质:两点之间线段最短.
【分析】根据两点之间,线段最短进行解答.
【解答】解:某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是两点之间线段最短.
故选:A.
【变式】
如图,经过刨平的木析上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线. 能解释这一实际问题的数学知识是( )
A.两点确定一条直线 B.两点之间线段最短
C.垂线段最短 D.在同一平面内,过一点有且只有一条直线与已知直线垂直
【答案】A.
【解析】
试题分析:根据公理“两点确定一条直线”,来解答即可:
经过刨平的木板上的两个点,能弹出一条笔直的墨线此操作的依据是两点确定一条直线.
故选A.
考点二、求线段的长度
【例题】如图,已知点C在线段AB上,点M、N分别是AC、BC的中点,且AB=8cm,则MN的长度为( )cm.
A.2 B.3 C.4 D.6
【考点】两点间的距离.
【分析】根据MN=CM+CN=AC+CB=(AC+BC)=AB即可求解.
【解答】解:∵M、N分别是AC、BC的中点,
∴CM=AC,CN=BC,
∴MN=CM+CN=AC+BC=(AC+BC)=AB=4.
故选C.
【变式】如图,已知C,D为线段AB上顺次两点,点M、N分别为AC与BD的中点,若AB=10,CD=4,求线段MN的长.
【考点】两点间的距离.
【分析】根据线段的和差,可得AC+BD,根据线段中点的性质,可得MC,ND,根据线段的和差,可得答案.
【解答】解:由AB=10,CD=4,
∴AC+BD=AB﹣CD=10﹣4=6.
∵M、N分别为AC与BD的中点
∴MC=AC,ND=BD
∴MC+ND=(AC+BD)=×6=3,
∴MN=MC+ND+CD=3+4=7.
考点三、求角的度数
【例题】(2016•宜昌)已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
A.∠NOQ=42° B.∠NOP=132°
C.∠PON比∠MOQ大 D.∠MOQ与∠MOP互补
【分析】根据已知量角器上各点的位置,得出各角的度数,进而得出答案.
【解答】解:如图所示:∠NOQ=138°,故选项A错误;
∠NOP=48°,故选项B错误;
如图可得:∠PON=48°,∠MOQ=42°,故∠PON比∠MOQ大,故选项C正确;
由以上可得,∠MOQ与∠MOP不互补,故选项D错误.
故选:C.
【点评】此题主要考查了余角和补角,正确得出各角的度数是解题关键.
【变式】如图,在直线AD上任取一点O,过点O作射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,∠BOE的度数是 64° .
【考点】角平分线的定义.
【分析】先根据角平分线的性质求出∠AOB的度数,再利用平角求出∠BOD的度数,利用OE平分∠DOB,即可解答.
【解答】解:∵OC平分∠AOB,∠BOC=26°,
∴∠AOB=2∠BOC=26°×2=52°,
∴∠BOD=180°﹣∠AOB=180°﹣52°=128°,
∵OE平分∠DOB,
∴∠BOE=BOD=64°.
故答案为:64°.
考点四、立体图形展开图
【例题】一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和“崇”相对的面上写的汉字是( )
A.低 B.碳 C.生 D.活
【考点】专题:正方体相对两个面上的文字.
【分析】根据正方形展开图相对的面应相隔一个面作答.
【解答】解:和“崇”相隔一个面的面为“低”,故选A.
【点评】解决本题的关键是理解正方体侧面展开图相对的面之间应相隔一个面.
【变式】用五个完全相同的小正方体组成如图所示的立体图形,从上面看到的图形是( )
A. B. C. D.
【考点】简单组合体的三视图.
【分析】根据从上边看得到的图形是俯视图,可得答案.
【解答】解:从上边看第一列是一个正方形,第二列是两个正方形,第三列是一个正方形,
故选:C.
考点五、平行线的性质和判定
【例题1】如图,已知a∥b,∠1=70°,∠2=40°,则∠3= 70 度.
【分析】把∠2,∠3转化为△ABC中的角后,利用三角形内角和定理求解.
【解答】解:由对顶角相等可得∠ACB=∠2=40°,
在△ABC中,由三角形内角和知∠ABC=180°﹣∠1﹣∠ACB=70°.
又∵a∥b,
∴∠3=∠ABC=70°.
故答案为:70.
【点评】本题考查了平行线与三角形的相关知识.
【例题2】如图所示,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为 平行 .
【分析】根据同位角相等,两直线平行判断.
【解答】解:根据题意,∠1与∠2是三角尺的同一个角,
所以∠1=∠2,
所以,AB∥CD(同位角相等,两直线平行).
故答案为:平行.
【点评】本题考查了平行线的判定熟练掌握同位角相等,两直线平行,并准确识图是解题的关键.
【变式】
如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )
A.50° B.55° C.60° D.65°
【分析】首先根据AD∥BC,求出∠FED的度数,然后根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,则可知∠FED=∠FED′,最后求得∠AED′的大小.
【解答】解:∵AD∥BC,
∴∠EFB=∠FED=65°,
由折叠的性质知,∠FED=∠FED′=65°,
∴∠AED′=180°﹣2∠FED=50°.
故∠AED′等于50°.
故选:A.
【点评】本题考查了:1、折叠的性质;2、矩形的性质,平行线的性质,平角的概念求解.
题型六、对顶角
【例题】
(2015吉林)图中是对顶角量角器,用它测量角的原理是 .
【答案】对顶角相等.
【解析】
试题分析:由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角.因为对顶角相等,所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.故答案为:对顶角相等.
【分析】根据对顶角相等.
【解析】由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角.因为对顶角相等,所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.故答案为:对顶角相等.
【点评】本题主要考查了利用对顶角相等解决实际问题.
【变式】
1. 下列命题中正确的有( )
①相等的角是对顶角; ②在同一平面内,若a∥b,b∥c,则a∥c;
③同旁内角互补; ④互为邻补角的两角的角平分线互相垂直.
A.0个 B.1个 C.2个 D.3个
【分析】根据对顶角的性质、平行公理、平行线的判定定理和垂直的定义对各个选项进行判断即可.
【解答】解:相等的角不一定是对顶角,①错误;
在同一平面内,若a∥b,b∥c,则a∥c,②正确;
同旁内角不一定互补,③错误;
互为邻补角的两角的角平分线互相垂直,④正确,
故选:C.
【点评】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
2.(2015•吉林,第10题3分)图中是对顶角量角器,用它测量角的原理是 对顶角相等 .
考点: 对顶角、邻补角.
专题: 应用题.
分析: 由题意知,一个破损的扇形零件的圆心角与其两边的反向延长线组的角是对顶角,根据对顶角的性质解答即可.
解答: 解:由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角.因为对顶角相等,所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.
故答案为:对顶角相等.
点评: 本题考查了对顶角的定义、性质,有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
【典例解析】
1.下列立体图形中,侧面展开图是扇形的是( )
A. B. C. D.
【考点】几何体的展开图.
【分析】圆锥的侧面展开图是扇形.
【解答】解:根据圆锥的特征可知,侧面展开图是扇形的是圆锥.
故选:B.
【点评】解题时勿忘记圆锥的特征及圆锥展开图的情形.
2.(2016•重庆)如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
A.120° B.110° C.100° D.80°
【分析】由平行线的性质得出∠1+∠DFE=180°,由对顶角相等求出∠DFE=∠2=80°,即可得出结果.
【解答】解:∵AB∥CD,
∴∠1+∠DFE=180°,
∵∠DFE=∠2=80°,
∴∠1=180°﹣80°=100°;
故选:C.
【点评】本题考查了平行线的性质、对顶角相等的性质;熟记平行线的性质,由对顶角相等求出∠DFE是解决问题的关键.
3.下列图形中,∠1和∠2互为余角的是( )
A. B. C. D.
【考点】余角和补角.
【分析】根据余角、补角的定义计算.
【解答】解:根据余角的定义,两角之和为90°,这两个角互余.
D中∠1和∠2之和为90°,互为余角.
故选D.
【点评】根据余角的定义来判断,记住两角之和为90°,与两角位置无关.
中考热点
热点1.如图所示,一个斜插吸管的盒装饮料从正面看的图形是( )
A. B. C. D.
【考点】简单组合体的三视图.
【分析】找到从正面看所得到的图形即可.
【解答】解:从正面可看到一个矩形右上角有一条线段,
故选A.
【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
热点2.将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为( )
A.60° B.75° C.90° D.95°
【考点】翻折变换(折叠问题).
【分析】根据图形,利用折叠的性质,折叠前后形成的图形全等.
【解答】解:∠ABC+∠DBE+∠DBC=180°,且∠ABC+∠DBE=∠DBC;故∠CBD=90°.
故选C.
【点评】本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.
热点3.我们已学习了角平分线的概念,那么你会用他们解决有关问题吗?
(1)如图1所示,将长方形笔记本活页纸片的一角折过去,使角的顶点A落在A′处,BC为折痕.若∠ABC=55°,求∠A′BD的度数.
(2)在(1)条件下,如果又将它的另一个角也斜折过去,并使BD边与BA′重合,折痕为BE,如图2所示,求∠2和∠CBE的度数.
(3)如果将图2中改变∠ABC的大小,则BA′的位置也随之改变,那么(2)中∠CBE的大小会不会改变?请说明.
【考点】角平分线的定义;角的计算;翻折变换(折叠问题).
【分析】(1)由折叠的性质可得∠A′BC=∠ABC=55°,由平角的定义可得∠A′BD=180°﹣∠ABC﹣∠A′BC,可得结果;
(2)由(1)的结论可得∠DBD′=70°,由折叠的性质可得==35°,由角平分线的性质可得∠CBE=∠A′BC+∠D′BE=×180°=90°;
(3)由折叠的性质可得,,∠2=∠EBD=∠DBD′,可得结果.
【解答】解:(1)∵∠ABC=55°,
∴∠A′BC=∠ABC=55°,
∴∠A′BD=180°﹣∠ABC﹣∠A′BC
=180°﹣55﹣55°
=70°;
(2)由(1)的结论可得∠DBD′=70°,
∴==35°,
由折叠的性质可得,
∴∠CBE=∠A′BC+∠D′BE=×180°=90°;
(3)不变,
由折叠的性质可得,
,∠2=∠EBD=∠DBD′,
∴∠1+∠2===90°,
不变,永远是平角的一半.
达标测试
一、选择题
1.下面四个图形中,∠1=∠2一定成立的是( )
A.B.C.D.
2.(2016•绍兴)如图是一个正方体,则它的表面展开图可以是( )
A. B. C. D.
3.(2016•宿迁)如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
A.50° B.60° C.120° D.130°
4.如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
A.4 B.6 C.8 D.10
5.如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB的度数等于( )
A.70° B.100° C.110° D.120°
6. 在同一平面内,下列说法正确的是( )
A.两直线的位置关系是平行、垂直和相交
B.不平行的两条直线一定互相垂直
C.不垂直的两条直线一定互相平行
D.不相交的两条直线一定互相平行
7.如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于( )
A.15° B.30° C.75° D.150°
8.如图,已知AB∥CD,∠A=50°,∠C=∠E,则∠C=( )
A、20° B、25° C、30° D、40°
E
A
D
B
50°
C
二、填空题
9. 已知∠A与∠B互余,若∠A=70°,则∠B的度数为 度.
10.(2013浙江湖州,12,4分)把15°30′化成度的形式,则15°30′=__ __度.
11.一个角的补角等于它的余角的6倍,则这个角
的度数为 .
12. (1)13°30'= °;
(2)0.5°= '= ″.
13.(2016·山东省菏泽市·3分)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 .
14. (2016·吉林·3分)如图,AB∥CD,直线EF分别交AB、CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于 度.
15. (2016·四川宜宾)如图,直线a∥b,∠1=45°,∠2=30°,则∠P= °.
16.如图,射线AB,CD分别与直线l相交于点G、H,若∠ 1=∠ 2,∠ C=65°,则∠ A的度数是 .
17. 已知点A、B、C在同一条直线上,且线段AB=5,BC=4,则A、C两点间的距离是 .
18.表反映了平面内直线条数与它们最多交点个数的对应关系:
图形
…
直线条数
2
3
4
…
最多交点个数
1
3=1+2
6=1+2+3
…
按此规律,6条直线相交,最多有个交点;n条直线相交,最多有 个交点.(n为正整数)
三、解答题:
19. 计算:
(1)40°26′+30°30′30″÷6;
(2)13°53′×3﹣32°5′31″.
20. 已知:C为线段AB的中点,D在线段BC上,且AD=7,BD=5,求:线段CD的长度.
21. 把一副三角板的直角顶点O重叠在一起.
(1)如图(1),当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图(2),当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
22. 探究题:
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.
(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.
答案与解析
【知识归纳】
(一)、直线、射线、线段
1.直线的性质: 1 、(2) 1
2.线段的性质: 线段
3.线段的中点性质: AB ;AB=2 BC =2 AC .
4.在同一平面内,两条直线只有两种位置关系: 相交 , 平行 .
5.垂线的性质:(1) 1 ;(2) 线段 .
6.点到直线的距离:点到这条直线的距离.
(二)角
1.角平分线的性质:∠BOC=∠AOB,∠AOB=2∠BOC=2∠AOC.
2.余角和补角的性质:相等;相等.
3.角度之间的转换关系:1°=60′,1′=60″,1°=3600″.
4.对顶角的性质:对顶角相等.
(三)三线八角同位角;内错角;同旁内角.
(四)平行线的性质
1.平行线公理: 1 .
2.平行线的基本性质:
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补
(五)平行线的判定方法
1.同位角相等,两直线平行;
2.内错角相等,两直线平行;
3.同旁内角互补,两直线平行;
4.传递性:如果a∥b,b∥c,那么a∥c
【基础检测答案】
1.(2017广东)已知∠A=70°,则∠A的补角为( )
A.110° B.70° C.30° D.20°
【考点】IL:余角和补角.
【分析】由∠A的度数求出其补角即可.
【解答】解:∵∠A=70°,
∴∠A的补角为110°,
故选A
2.(2017浙江湖州)七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那副图是( )
A.B.C.D.
【考点】IM:七巧板.
【分析】解答此题要熟悉七巧板的结构:五个等腰直角三角形,有大、小两对全等三角形;一个正方形;一个平行四边形,根据这些图形的性质便可解答.
【解答】解:图C中根据图7、图4和图形不符合,故不是由原图这副七巧板拼成的.
故选C
3.(2017•宁德)如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
A.BM=AB B.AM+BM=AB C.AM=BM D.AB=2AM
【考点】ID:两点间的距离.
【分析】直接利用两点之间的距离定义结合线段中点的性质分别分析得出答案.
【解答】解:A、当BM=AB时,则M为AB的中点,故此选项错误;
B、AM+BM=AB时,无法确定M为AB的中点,符合题意;
C、当AM=BM时,则M为AB的中点,故此选项错误;
D、当AB=2AM时,则M为AB的中点,故此选项错误;
故选:B.
【点评】此题主要考查了两点之间,正确把握线段中点的性质是解题关键.
4. (2017湖北江汉)如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
A.传 B.统 C.文 D.化
【考点】I8:专题:正方体相对两个面上的文字.
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:这是一个正方体的平面展开图,共有六个面,其中面“扬”与“统”相对,面“弘”与面“文”相对,“传”与面“化”相对.
故选:C.
5. (2017•黑龙江)几个相同的小正方体所搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置小正方体的个数最多是( )
俯视图 左视图
A.5个 B.7个 C.8个 D.9个
【考点】U3:由三视图判断几何体.
【分析】根据俯视图知几何体的底层有4个小正方形组成,而左视图是由3个小正方形组成,故这个几何体的后排最有1个小正方体,前排最多有2×3=6个小正方体,即可解答.
【解答】解:由俯视图及左视图知,构成该几何体的小正方形体个数最多的情况如下:
故选:B.
【点评】本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就容易得到答案.
6. (2017贵州安顺)如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
【考点】JA:平行线的性质.
【分析】先根据互余计算出∠3=90°﹣40°=50°,再根据平行线的性质由a∥b得到∠2=180°﹣∠3=130°.
【解答】解:∵∠1+∠3=90°,
∴∠3=90°﹣40°=50°,
∵a∥b,
∴∠2+∠3=180°.
∴∠2=180°﹣50°=130°.
故选:D.
【达标检测答案】
一、选择题
1.下面四个图形中,∠1=∠2一定成立的是( )
A. B.C.D.
【分析】根据对顶角、邻补角、平行线的性质及三角形的外角性质,可判断;
【解答】解:A、∠1、∠2是邻补角,∠1+∠2=180°;故本选项错误;
B、∠1、∠2是对顶角,根据其定义;故本选项正确;
C、根据平行线的性质:同位角相等,同旁内角互补,内错角相等;故本选项错误;
D、根据三角形的外角一定大于与它不相邻的内角;故本选项错误.
故选B.
【点评】本题考查了对顶角、邻补角、平行线的性质及三角形的外角性质,本题考查的知识点较多,熟记其定义,是解答的基础.
2.(2016•绍兴)如图是一个正方体,则它的表面展开图可以是( )
A. B. C. D.
【分析】根据含有田字形和凹字形的图形不能折成正方体可判断A、C,D,故此可得到答案.
【解答】解:A、含有田字形,不能折成正方体,故A错误;
B、能折成正方体,故B正确;
C、凹字形,不能折成正方体,故C错误;
D、含有田字形,不能折成正方体,故D错误.
故选:B.
【点评】本题主要考查的是几何体的展开图,明确含有田字形和凹字形的图形不能折成正方体是解题的关键.
3.(2016•宿迁)如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
A.50° B.60° C.120° D.130°
【分析】根据邻补角的定义求出∠3,再根据两直线平行,同位角相等解答.
【解答】解:如图,∠3=180°﹣∠1=180°﹣120°=60°,
∵a∥b,
∴∠2=∠3=60°.
故选:B.
【点评】本题考查了平行线的性质,邻补角的定义,是基础题,熟记性质是解题的关键.
4.如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
A.4 B.6 C.8 D.10
【答案】D.
【解析】∵C为AB的中点,∴AC=BC=AB=×12=6,
∵AD:CB=1:3,∴AD=2,
∴DB=AB-AD=12-2=10(cm).
故选D.
5.如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB的度数等于( )
A.70° B.100° C.110° D.120°
【答案】C.
【解析】∵DE∥AC,∠ BDE=60°,∠C=50°,∴∠BDE=∠A=60°,
∴∠BDC=∠A+∠C=60°+50°=110°.
故选C.
6. 在同一平面内,下列说法正确的是( )
A.两直线的位置关系是平行、垂直和相交
B.不平行的两条直线一定互相垂直
C.不垂直的两条直线一定互相平行
D.不相交的两条直线一定互相平行
【分析】在同一平面内,两直线的位置关系有2种:平行、相交,根据以上结论判断即可.
【解答】解:A、∵在同一平面内,两直线的位置关系是平行、相交,2种,
∴在同一平面内,两直线的位置关系是平行、相交(相交不一定垂直),故本选项错误;
B、在同一平面内,不平行的两条直线一定相交,故本选项错误;
C、在同一平面内,不垂直的两直线可能平行,可能相交,故本选项错误;
D、在同一平面内,不相交的两条直线一定平行,故本选项正确;
故选D.
【点评】本题考查了对平行线的理解和运用,注意:①在同一平面内,两直线的位置关系有2种:平行、相交,②相交不一定垂直.
7.如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于( )
A.15° B.30° C.75° D.150°
【答案】A.
【解析】∵直线AB∥CD,∠BNE=30°,∴∠DME=∠BNE=30°.∵MG是∠EMD的角平分线,∴∠EMG=∠EMD=15°.故选A.
8.如图,已知AB∥CD,∠A=50°,∠C=∠E,则∠C=( )
A、20° B、25° C、30° D、40°
E
A
D
B
50°
C
【答案】B.
【解析】如图:
∵AB∥CD
∴∠1=∠A=50°
而∠1=∠C+∠E
又∠C=∠E
∴∠C=25°
故选B.
二、填空题
9. 已知∠A与∠B互余,若∠A=70°,则∠B的度数为 20 度.
【考点】余角和补角.
【专题】计算题.
【分析】根据余角定义直接解答.
【解答】解:∠B=90°﹣70°=20°.
【点评】本题比较容易,考查互余角的数量关系.根据余角的定义可得∠B=90°﹣70°=20度.
10.(2013浙江湖州,12,4分)把15°30′化成度的形式,则15°30′=__▲__度.
【答案】15.5
【解析】15°30′=15°+=15.5°,故填15.5
【方法指导】本题考查了角的单位:度分秒的换算。由高级单位变成低级单位乘以进率,由低级单位变成高级单位除以进率。
11.一个角的补角等于它的余角的6倍,则这个角
的度数为 72° .
【考点】余角和补角.
【分析】利用题中的关系“一个角的补角等于这个角的余角的6倍”作为相等关系列方程求解即可.
【解答】解:设这个角为x,则它的补角为(180°﹣x)
余角为(90°﹣x),由题意得:
180°﹣x=6(90°﹣x),
180°﹣x=540°﹣6x,
6x﹣x=540°﹣180°,
5x=360°,
x=72°.
答:这个角的度数为72°.
故答案为:72°.
【点评】主要考查了利用余角和补角的定义和一元一次方程的应用.解此题的关键是能准确的从题中找出各个量之间的数量关系,找出等量关系列方程,从而计算出结果.互为余角的两角的和为90°,互为补角的两角之和为180度.
12. (1)13°30'= 13.5 °;
(2)0.5°= 30 '= 1800 ″.
【考点】度分秒的换算.
【分析】(1)根据度分秒的换算,将30′换算成0.5°即可得出结论;
(2)根据度分秒的换算,将0.5°换算成30′,再将30′换算成1800″即可得出结论.
【解答】解:(1)13°30'=13°+()°=13.5°;
(2)0.5°=(0.5×60)′=30′=(30×60)″=1800″.
故答案为:(1)13.5;(2)30;1800.
【点评】本题考查了度分秒的换算,熟练的掌握度分秒的进率是解题的关键.
13.(2016·山东省菏泽市·3分)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 15° .
【考点】平行线的性质.
【专题】计算题.
【分析】过A点作AB∥a,利用平行线的性质得AB∥b,所以∠1=∠2,∠3=∠4=30°,加上∠2+∠3=45°,易得∠1=15°.
【解答】解:如图,过A点作AB∥a,
∴∠1=∠2,
∵a∥b,
∴AB∥b,
∴∠3=∠4=30°,
而∠2+∠3=45°,
∴∠2=15°,
∴∠1=15°.
故答案为15°.
【点评】本题考查了平行线的性质:两直线平行,内错角相等.
14. (2016·吉林·3分)如图,AB∥CD,直线EF分别交AB、CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于 30 度.
【考点】平行线的性质.
【分析】根据平行线的性质得到∠DNM=∠BME=75°,由等腰直角三角形的性质得到∠PND=45°,即可得到结论.
【解答】解:∵AB∥CD,
∴∠DNM=∠BME=75°,
∵∠PND=45°,
∴∠PNM=∠DNM﹣∠DNP=30°,
故答案为:30.
15. (2016·四川宜宾)如图,直线a∥b,∠1=45°,∠2=30°,则∠P= 75 °.
【考点】平行线的性质.
【分析】过P作PM∥直线a,求出直线a∥b∥PM,根据平行线的性质得出∠EPM=∠2=30°,∠FPM=∠1=45°,即可求出答案.
【解答】解:
过P作PM∥直线a,
∵直线a∥b,
∴直线a∥b∥PM,
∵∠1=45°,∠2=30°,
∴∠EPM=∠2=30°,∠FPM=∠1=45°,
∴∠EPF=∠EPM+∠FPM=30°+45°=75°,
故答案为:75.
16.如图,射线AB,CD分别与直线l相交于点G、H,若∠ 1=∠ 2,∠ C=65°,则∠ A的度数是 .
【答案】115°.
【解析】∵∠ 1=∠ BGH,∠ 1=∠ 2,∴∠ BGH=∠ 2,
∴AB∥ CD,∴∠ A+∠ C=180°,
∵∠ C=65°,∴∠ A=115°.
17. 已知点A、B、C在同一条直线上,且线段AB=5,BC=4,则A、C两点间的距离是 1或9 .
【考点】两点间的距离.
【分析】根据线段的和差,可得答案.
【解答】解:当C在线段AB上时,AC=AB﹣BC=5﹣4=1,
当 C在线段AB的延长线上时,AC=AB+BC=5+4=9,
故答案为:1或9.
16.表反映了平面内直线条数与它们最多交点个数的对应关系:
图形
…
直线条数
2
3
4
…
最多交点个数
1
3=1+2
6=1+2+3
…
按此规律,6条直线相交,最多有个交点;n条直线相交,最多有 个交点.(n为正整数)
【考点】直线、射线、线段.
【分析】根据观察,可发现规律:n条直线最多的交点是1+2+3+(n﹣1),可得答案.
【解答】解:6条直线相交,最多有个交点1+2+3+4+5=15;
n条直线相交,最多有个交点,
故答案为:15,.
三、解答题:
18. 计算:
(1)40°26′+30°30′30″÷6;
(2)13°53′×3﹣32°5′31″.
【考点】度分秒的换算.
【专题】计算题.
【分析】(1)先进行度、分、秒的除法计算,再算加法.
(2)先进行度、分、秒的乘法计算,再算减法.
【解答】解:(1)40°26′+30°30′30″÷6=40°26′+5°5′5″=45°31′5″;
(2)13°53′×3﹣32°5′31″=41°39′﹣32°5′31″=9°33′29″.
【点评】此类题是进行度、分、秒的四则混合运算,是角度计算中的一个难点,注意以60为进制即可.
19. 已知:C为线段AB的中点,D在线段BC上,且AD=7,BD=5,求:线段CD的长度.
【考点】比较线段的长短.
【专题】计算题.
【分析】根据已知可求得AB的长,从而可求得AC的长,已知AD的长则不难求得CD的长.
【解答】解:∵AD=7,BD=5
∴AB=AD+BD=12
∵C是AB的中点
∴AC=AB=6
∴CD=AD﹣AC=7﹣6=1.
【点评】此题主要考查学生对比较线段的长短的掌握情况,比较简单.
20. 把一副三角板的直角顶点O重叠在一起.
(1)如图(1),当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图(2),当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
【考点】角平分线的定义.
【分析】已知一副三角板的直角顶点O重叠在一起,就是已知图形中的两个三角形各角的度数,这样重叠时存在的角的关系是:∠AOD=∠AOB+∠COD﹣∠COB.
【解答】解:(1)∵OB平分∠COD,
∴∠COB=∠BOD=45°,
∴∠COA=90°﹣45°=45°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC
=45°+90°+45°=180°,
∴∠AOD和∠BOC的和是180°.
(2)∵∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,
∴∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC
∴∠AOD+∠BOC=(∠AOC+∠BOC)+(∠BOD+∠BOC)
=90°+90°=180°.
∴∠AOD和∠BOC的和是180°.
【点评】根据角平分线定义得出所求角与已知角的关系转化求解.注意一副三角板的直角顶点O重叠在一起时角的关系.
21. 推理填空:如图:
①若∠1=∠2,
则 AD ∥ CB (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 AD ∥ BC (同旁内角互补,两直线平行);
②当 AB ∥ CD 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 AD ∥ BC 时,
∠3=∠C (两直线平行,同位角相等).
【分析】根据平行线的性质和平行线的判定直接完成填空.两条直线平行,则同位角相等,内错角相等,同旁内角互补;反之亦成立.
【解答】解:①若∠1=∠2,
则AD∥CB(内错角相等,两条直线平行);
若∠DAB+∠ABC=180°,
则AD∥BC(同旁内角互补,两条直线平行);
②当AB∥CD时,
∠C+∠ABC=180°(两条直线平行,同旁内角互补);
③当AD∥BC时,
∠3=∠C (两条直线平行,同位角相等).
【点评】在做此类题的时候,一定要细心观察,看两个角到底是哪两条直线被第三条直线所截而形成的角.
22. 探究题:
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.
(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.
【分析】(1)首先作EF∥AB,根据AB∥CD,可得EF∥CD,据此分别判断出∠B=∠1,∠D=∠2,即可判断出∠B+∠D=∠E,据此解答即可.
(2)首先作EF∥AB,即可判断出∠B=∠1;然后根据∠E=∠1+∠2=∠B+∠D,可得∠D=∠2,据此判断出EF∥CD,再根据EF∥AB,可得AB∥CD,据此判断即可.
(3)首先过E作EF∥AB,即可判断出∠BEF+∠B=180°,然后根据EF∥CD,可得∠D+∠DEF=180°,据此判断出∠E+∠B+∠D=360°即可.
(4)首先根据AB∥CD,可得∠B=∠BFD;然后根据∠D+∠E=∠BFD,可得∠D+∠E=∠B,据此解答即可.
(5)首先作EM∥AB,FN∥AB,GP∥AB,根据AB∥CD,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,所以∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;然后根据∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,可得∠E+∠G=∠B+∠F+∠D,据此判断即可.
【解答】解:(1)如图1,作EF∥AB,
,
∵AB∥CD,
∴∠B=∠1,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠D=∠2,
∴∠B+∠D=∠1+∠2,
又∵∠1+∠2=∠E,
∴∠B+∠D=∠E.
(2)如图2,作EF∥AB,,
∵EF∥AB,
∴∠B=∠1,
∵∠E=∠1+∠2=∠B+∠D,
∴∠D=∠2,
∴EF∥CD,
又∵EF∥AB,
∴AB∥CD.
(3)如图3,过E作EF∥AB,,
∵EF∥AB,
∴∠BEF+∠B=180°,
∵EF∥CD,
∴∠D+∠DEF=180°,
∵∠BEF+∠DEF=∠E,
∴∠E+∠B+∠D=180°+180°=360°.
(4)如图4,,
∵AB∥CD,
∴∠B=∠BFD,
∵∠D+∠E=∠BFD,
∴∠D+∠E=∠B.
(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,
又∵AB∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;
∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,
∴∠E+∠G=∠B+∠F+∠D.
【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.
2018年数学中考第一轮复习讲义:2018年数学中考第一轮复习讲义:第4讲 二次根式: 这是一份2018年数学中考第一轮复习讲义:2018年数学中考第一轮复习讲义:第4讲 二次根式,共19页。
2018年数学中考第一轮复习讲义:2018年数学中考第一轮复习讲义:第8讲 分式方程: 这是一份2018年数学中考第一轮复习讲义:2018年数学中考第一轮复习讲义:第8讲 分式方程,共29页。试卷主要包含了分式方程,解分式方程的一般步骤,分式方程的应用,关于的方程等内容,欢迎下载使用。
2018年数学中考第一轮复习讲义:2018年数学中考第一轮复习讲义:第15讲 反比例函数: 这是一份2018年数学中考第一轮复习讲义:2018年数学中考第一轮复习讲义:第15讲 反比例函数,共57页。试卷主要包含了k的几何意义等内容,欢迎下载使用。












