初中数学沪科版九年级上册23.1 锐角的三角函数教学演示课件ppt

这是一份初中数学沪科版九年级上册23.1 锐角的三角函数教学演示课件ppt，共30页。PPT课件主要包含了答案显示，核心必知，见习题，答案A等内容，欢迎下载使用。

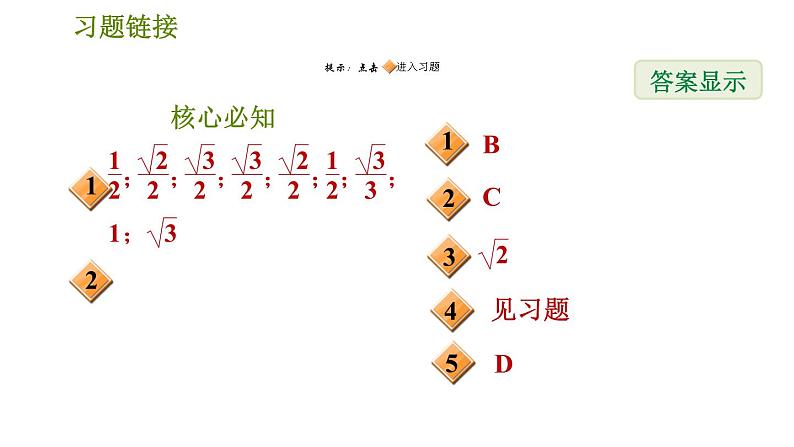
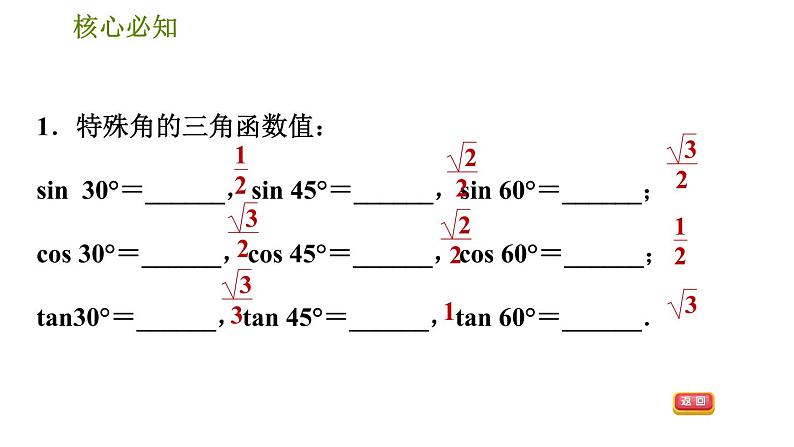
1．特殊角的三角函数值：sin 30°＝______，sin 45°＝______，sin 60°＝______；cs 30°＝______，cs 45°＝______，cs 60°＝______；tan30°＝______，tan 45°＝______，tan 60°＝______．
2．任意一个锐角的正(余)弦值，等于它的余角的余(正)弦值．
1．【2020·天津】2sin 45°的值等于(　　)A．1　　　　 B.　　　　 C.　　　　 D．2
2．如图，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，则sin ∠AOB的值等于(　　)
3．在△ABC中，∠C＝90°，若∠A＝45°，则cs A＋sin B的值等于__________．
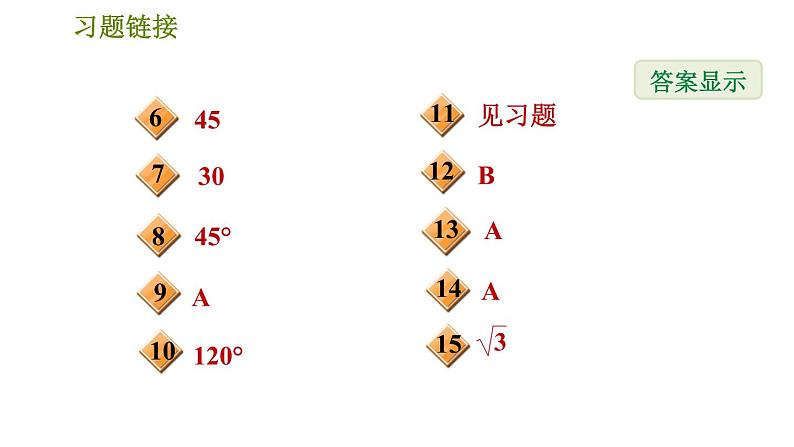
5．【蚌埠期末】在Rt△ABC中，∠C＝90°，BC＝ ，AC＝ ，则∠A＝(　　)A．90° B．60° C．45° D．30°
6．【铜陵期末】已知α为锐角，tan α＝2sin 30°，那么α＝________°.
7．【合肥蜀山区期末】已知斜坡AB的坡度i＝1∶ ，则斜坡AB的坡角是________度．
8．当α为锐角时， 无意义，则α的度数为________．
9．【2019·合肥包河区模拟】如图，在△ABC中，∠C＝90°，cs A＝ ，则sin B＝(　　)
10．【2019·合肥包河区期末】在△ABC中，sin B＝cs (90°－∠C)＝ ，则∠A的大小是________．
11．已知α和β都是锐角，且α＋β＝90°，sin α＋cs β＝ ，求锐角α.
12．若等腰三角形的腰长和底边长之比为1∶ ，则它的底角和顶角的度数分别是(　　)A．30°和120° B．45°和90°C．60°和60° D．15°和150°
A．直角三角形B．等边三角形C．含60°角的任意三角形D．顶角为钝角的等腰三角形
14．【中考·包头】如图，点O在△ABC内，且到三边的距离相等，若∠BOC＝120°，则tan A的值为(　　)
15．定义：在Rt△ABC中，∠C＝90°，∠A的邻边与对边的比叫做∠A的余切，记作ct A，即ct A＝ ，根据上述角的余切概念，可知ct 30°＝________．
16．【2020·安庆模拟】在△ABC中，若∠A，∠B满足 ＋(1－tan B)2＝0，则∠C的大小是________．
17.计算：(1)【2021·淮北五校联考】8 sin260°＋tan 45°－4 cs 30°；
(2) ＋(tan 70°－sin 10°)0＋sin 60°·tan 30°；
18．在△ABC中，已知∠A＝60°，∠B为锐角，且tan A，cs B恰为一元二次方程2x2－3mx＋3＝0的两个实数根．求m的值，并判断△ABC的形状．
19．同学们，在我们进入高中以后，将会学到下面的三角函数公式：sin (α－β)＝sin αcs β－cs αsin β，cs (α－β)＝cs αcs β＋sin αsin β.例：sin 15°＝sin (45°－30°)＝sin 45°cs 30°－cs 45°·sin 30°＝ .
(1)试利用上面的公式，求出cs 15°的值；