河北省邯郸市2021年中考数学五模试卷附答案

这是一份河北省邯郸市2021年中考数学五模试卷附答案，共11页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


中考数学五模试卷
一、单选题（共16题；共32分）
1.如下字体的四个汉字中，可以看作是轴对称图形的是（    ）
A.                                B.                                C.                                D. 
2.下列二次根式是最简二次根式的是（    ）.
A.                                       B.                                       C.                                       D. 
3.图中的两个三角形是位似图形，它们的位似中心是（    ）

A. 点P                                      B. 点D                                      C. 点M                                      D. 点N
4.斑叶兰被列为国家二级保护植物，它的一粒种子重约0.0000005克．将0.0000005用科学记数法表示为（   ）

A. 5×107                            B. 5×10﹣7                            C. 0.5×10﹣6                            D. 5×10﹣6
5.如图，在量角器的圆心 处下挂一铅锤，制作了一个简易测倾仪．量角器的0刻度线 对准楼顶时，铅垂线对应的读数是50°，则此时观察楼顶的仰角度数是（    ）．

A. 30°                                       B. 40°                                       C. 50°                                       D. 60°
6.下列多项式中，不能进行因式分解的是（    ）
A.                         B.                         C.                         D. 
7.如图，已知△ABC(AB＜BC＜AC)，用尺规在AC上确定一点P，使PB+PC＝AC，则下列选项中，一定符合要求的作图痕迹是(   )

A.        B.        C.        D. 
8.下列等式成立的是（    ）．
A.                    B.                    C.                    D. 
9.若关于x的一元二次方程 有两个不相等的实数根,则实数k的取值范围是（   ）
A.                           B. 且                           C.                           D. 且
10.如图，在 中， ， 是斜边 上的中线， 、 分别为 、 的中点．若 ，则AB的长是（    ）．

A. 4                                           B. 2                                           C. 1                                           D. 6
11.疫情无情人有情，爱心捐款传真情，新型冠状病毒感染的肺炎疫情期间，某班学生积极参加献爱心活动，该班50名学生的捐款统计情况如下表：
金额/元
5
10
20
50
100
人数
6
17
14
8
5
则他们捐款金额的众数和中位数和平均数分别是（    ）
A. 20，10，27.6                   B. 10，20，27.6                   C. 10，10，37                   D. 10，20，37
12.如图，数轴上标有 、 、 、 四个点，对应的数分别是a、b、c、d．有下列结论：
甲：若点 为原点，则 与 互为相反数；
乙：若点 为原点，则 ；
丙：若点 为原点，则点 到原点的距离与点 到原点的距离相等；
丁：若线段 的中点为原点，则 与 互为倒数．
其中正确的是（    ）．

A. 甲、乙                                B. 甲、丙                                C. 乙、丙                                D. 丙、丁
13.已知 和 有相同的外心， ，则 的度数是（    ）．
A. 80°                              B. 100°                              C. 80°或100°                              D. 不能确定．
14.反比例函数 过点 ， ，若 ，则 的取值范围为（    ）．
A.                              B.                              C.                              D. 
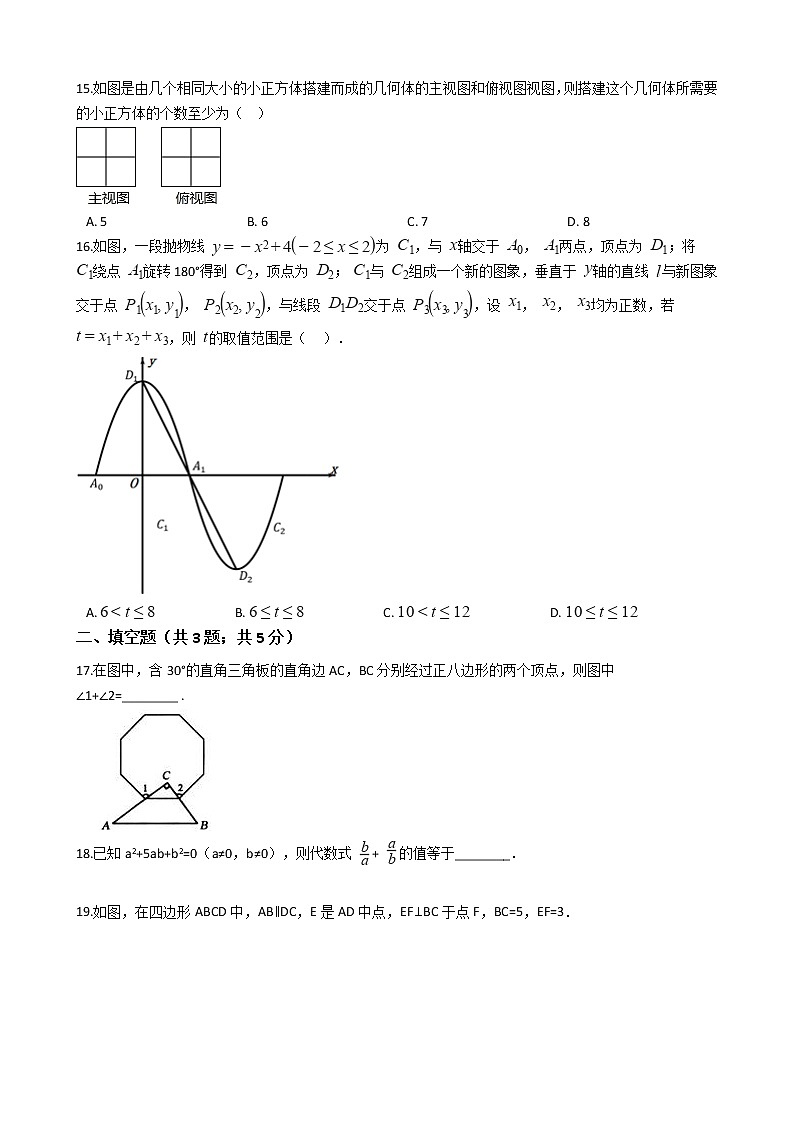
15.如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图视图，则搭建这个几何体所需要的小正方体的个数至少为（   ）

A. 5                                           B. 6                                           C. 7                                           D. 8
16.如图，一段抛物线 为 ，与 轴交于 ， 两点，顶点为 ；将 绕点 旋转180°得到 ，顶点为 ； 与 组成一个新的图象，垂直于 轴的直线 与新图象交于点 ， ，与线段 交于点 ，设 ， ， 均为正数，若 ，则 的取值范围是（    ）．

A.                          B.                          C.                          D. 
二、填空题（共3题；共5分）
17.在图中，含30°的直角三角板的直角边AC，BC分别经过正八边形的两个顶点，则图中∠1+∠2=________ .

18.已知a2+5ab+b2=0（a≠0，b≠0），则代数式 + 的值等于________．

19.如图，在四边形ABCD中，AB∥DC，E是AD中点，EF⊥BC于点F，BC=5，EF=3．


（1）若AB=DC，则四边形ABCD的面积S=________；

（2）若AB＞DC，则此时四边形ABCD的面积S′________ S（用“＞”或“=”或“＜”填空）．

三、解答题（共7题；共71分）
20.小刚在计算一个多项式 减去多项式 的差时，因一时疏忽忘了把两个多项式用括号括起来，因此减式后面两项没有变号，结果得到的差是 ．
（1）求这个多项式 ；
（2）求出这两个多项式运算的符合题意结果；
（3）当 时，求（2）中结果的值．
21.有个写运算符号的游戏：在“3□（2□3）□ □2” 中的每个□内，填入+，-，×，÷中的某一个（可重复使用），然后计算结果．
（1）请计算琪琪填入符号后得到的算式： ；
（2）嘉嘉填入符号后得到的算式是 □ ，一不小心擦掉了□里的运算符号，但她知道结果是 ，请推算□内的符号．
22.为了激励学生热爱数学，刻苦钻研，马鞍山市某学校八年级举行了一次数学竞赛，成绩由低到高分为 五个等级．竞赛结束后老师随机抽取了部分学生的成绩情况绘制成如下的条形图和扇形图，请根据提供的信息解答以下问题．

（1）补全条形统计图和统计扇形图．
（2）在本次抽样调查中，成绩的众数和中位数分别处于哪个等级？
（3）成绩为 等级的五个人中有 名男生 名女生，若从中任选两人，则两人恰好是一男一女的概率为多少？
23.如图，已知 是 的直径， ， 与圆交于点 ，过点 作 于点 ，与 的延长线交于点 ．

（1）求证： 是 的切线；
（2）若 半径长为3， ，求 的长；
（3）若 与圆交于点 ， 为 的中点， ，求 的度数．
24.如图，直线 与 轴、 轴交于点 、 ，直线 与 轴 轴分别交于点 、 ，两直线相交于点 ．

（1）求 ， 的值；
（2）求 的值；
（3）垂直于 轴的直线 与直线 ， 分别交于点 ， ，若线段 的长为2，求 的值．
25.某大学生利用暑假40天社会实践参与了一家网店经营，了解到一种新型商品成本为20元/件，第 天销售量为 件，销售单价为 元．经跟踪调查发现，这40天中 与 成正比，前20天（包含第20天）， 与 的关系满足关系式 ；从第21天到第40天中， 是基础价与浮动价的和，其中基础价保持不变，浮动价与 成反比，且得到了表中的数据：
（天）
10
21
35
（元/件）
35
45
35
（件）
40


（1）请直接写出 的值为________；直接写出这40天中 与 的关系式为________；
（2）从第21天到第40天中，求 与 满足的关系式；
（3）求这40天里该网店第几天获得的利润最大？最大为多少？
26.如图1， 在平行四边形 中， ， ， ，点 在 边上，且 ，点 在 边上，由点 向点 运动，以 为边在平行四边形 内部作等边 ，连接 ， ， ，设 ．

（1）判断 与 的数量关系： ________ ；
（2）若 ，①求 到 的距离；
②求 的面积；
（3）求出 的面积与 的关系．

答案解析部分
一、单选题
1.【答案】 A
2.【答案】 B
3.【答案】 A
4.【答案】 B
5.【答案】 B
6.【答案】 B
7.【答案】 C
8.【答案】 B
9.【答案】 B
10.【答案】 A
11.【答案】 B
12.【答案】 A
13.【答案】 C
14.【答案】 B
15.【答案】 B
16.【答案】 D
二、填空题
17.【答案】 180°
18.【答案】 -5
19.【答案】 （1）15
（2）=
三、解答题
20.【答案】 （1）解： ，


（2）解：
（3）解：当 时，原式
21.【答案】 （1）
=
=
=

（2）
=
=
= ,
因为 □2 = ，即 □4=
所以 =
所以“□”里应是“－”号．
22.【答案】 （1）解：由统计图信息可知：D等级人数所占百分比=1-40％-20％-10％-5％=25％
抽取学生的总人数=5÷5％=100（人），
D等级人数=100×25％=25（人）．
补全条形统计图和扇形统计图，如图所示：


（2）解：∵本次调查的人数为 人，根据条形统计图可知：成绩由低到高排序后，第50人和第51人的成绩都在C等级，且C等级的人数最多，
∴成绩的中位数和众数均处于 等级

（3）解：将三名男生分别标记为 将两名女生分别标记为 ．
列表如下：




































根据表格可知从中任选两人，共有20种等可能的结果，两人恰好是一男一女的共有12种，
∴P（两人恰好是一男一女） ．
23.【答案】 （1）证明：如图，连接 ，

∵ ，∴ ，
又∵ ，∴ ，
∴ ，∴ ，
∵ ，∴ ，
又∵ 在圆上（ 为半径），∴ 是 的切线

（2）解：由（1）得 ，∴ ，
∴ ，
在 中， ，
∵ ，∴ ，
∴ ，∴

（3）解：如图，连接 ，

∵ 为 的中点，且 ，
∴ 垂直平分 ，∴ ，∴ ，
∵ ，∴ ，
∴
24.【答案】 （1）解：∵点 在直线 上，∴ ，
∵ 在直线 上，∴ ，∴

（2）解：∵直线 与 轴、 轴交于点 、 ，
∴ ， ，
∵直线 与 轴、 轴分别交于点 、 ，
∴ ， ，
∴

（3）解：设直线 与直线 ， 分别交于点 ， ，
当 时， ；当 时， ，
∵ ，∴ ，解得 或 ，
所以 的值为 或
25.【答案】 （1）；p=-x+50
（2）解：从第21天到第40天中， 是基础价与浮动价的和，
其中基础价保持不变，浮动价与 成反比，
设 ，将 和 分别代入得 ，解得 ，
所以

（3）解：设利润为 ，则 ，
前20天，即 时，
，
∴当 时， 有最大值，最大值为 ．
第21天到第40天，即 时，
，
∵ 随 的增大而减小，∴当 时， 有最大值,最大值为725元，
综上所述，这40天里该网店第21天获得的利润最大，为725元
26.【答案】 （1）＝
（2）解：①如图，过点 作 垂直于 ，交 的延长线于点 ，

∵ ， ，
∴ ，
在 中，
∵ ，
∴ ．
②当 时，在 中， ， ，
如图，过点 作 于点 ，

则 ， ，
∴ ，
∴ ，
∴ 的面积

（3）解：如图，过点 作直线 的垂线，垂足为点 ，则 ，

在 中， ， ，
∴ ， ，
在 中， ，
∴