






- 2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题九 反比例函数与几何图形综合题 (共36张PPT) 课件 0 次下载
- 2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题二 实数、整式、分式的运算与化简求值 (共21张PPT) 课件 0 次下载
- 2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题七 函数的应用 (共40张PPT) 课件 0 次下载
- 2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题三 简单的几何证明与计算 (共35张PPT) 课件 0 次下载
- 2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题十 与几何图形有关的探究题 (共38张PPT) 课件 0 次下载
2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题八 解直角三角形的应用 (共29张PPT)
展开解直角三角形的应用是中考必考题型,常在解答题中考查,其中所给角度均为特殊角,涉及夹角、仰角、俯角、坡角等问题.常需添加辅助线,将所给图形转化为直角三角形或矩形来解决.预计2018年仍会在解答题中出现.
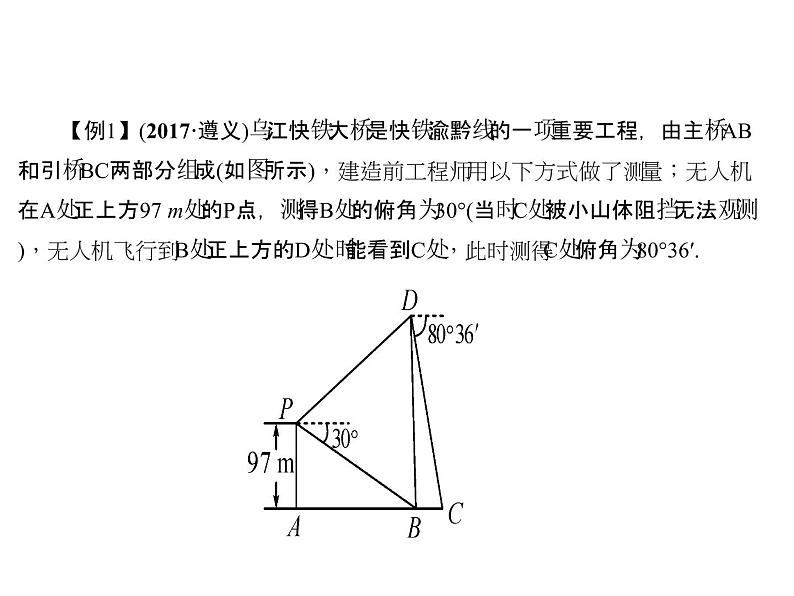
【例1】(2017·遵义)乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示),建造前工程师用以下方式做了测量;无人机在A处正上方97 m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测),无人机飞行到B处正上方的D处时能看到C处,此时测得C处俯角为80°36′.
【思路引导】过点O作OC⊥AB于点C,由已知可得△ABO中∠A=60°,∠B=45°且OA=80 m,要求OB的长,可以先求出OC和BC的长.
【思路引导】过点M作MF⊥PQ于点F,过点Q作QE⊥MN于点E,则四边形EMFQ是矩形.分别在Rt△EQN,Rt△PFM中解直角三角形即可解决问题.
4.(2017·贵阳)贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数.(结果精确到1°)
6.(导学号65244259)(2017·乌鲁木齐)一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cs37°≈0.8,≈1.732,结果取整数)
7.(导学号65244260)(2017·威海)图①是太阳能热水器装置的示意图,利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算:
如图②,AB⊥BC,垂足为点B,EA⊥AB,垂足为点A,CD∥AB,CD=10 cm,DE=120 cm,FG⊥DE,垂足为点G.(1)若∠θ=37°50′,则AB的长约为83.2cm;(参考数据:sin37°50′≈0.61,cs37°50′≈0.79,tan37°50′≈0.78)(2)若FG=30 cm,∠θ=60°,求CF的长.
2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题十 与几何图形有关的探究题 (共38张PPT): 这是一份2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题十 与几何图形有关的探究题 (共38张PPT),共38页。
2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题六 圆的有关证明与计算 (共41张PPT): 这是一份2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题六 圆的有关证明与计算 (共41张PPT),共41页。
2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题三 简单的几何证明与计算 (共35张PPT): 这是一份2018年中考数学(全国)总复习精英课件: 第二轮专题总复习 专题三 简单的几何证明与计算 (共35张PPT),共35页。












