
数学第五章 相交线与平行线综合与测试随堂练习题
展开1.下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短
2.如图,OA⊥OB,若∠BOC=34°20',则∠AOC的度数是( )
A.55°20'B.55°40'C.55°60'D.55°80'
3.如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
A.5050m2B.5000m2C.4900m2D.4998m2
4.已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是( )
A.相交B.平行C.垂直D.平行或相交
5.下列选项中∠1与∠2不是同位角的是( )
A. B. C. D.
6.如图,将Rt△ABC沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.42B.96C.84D.48
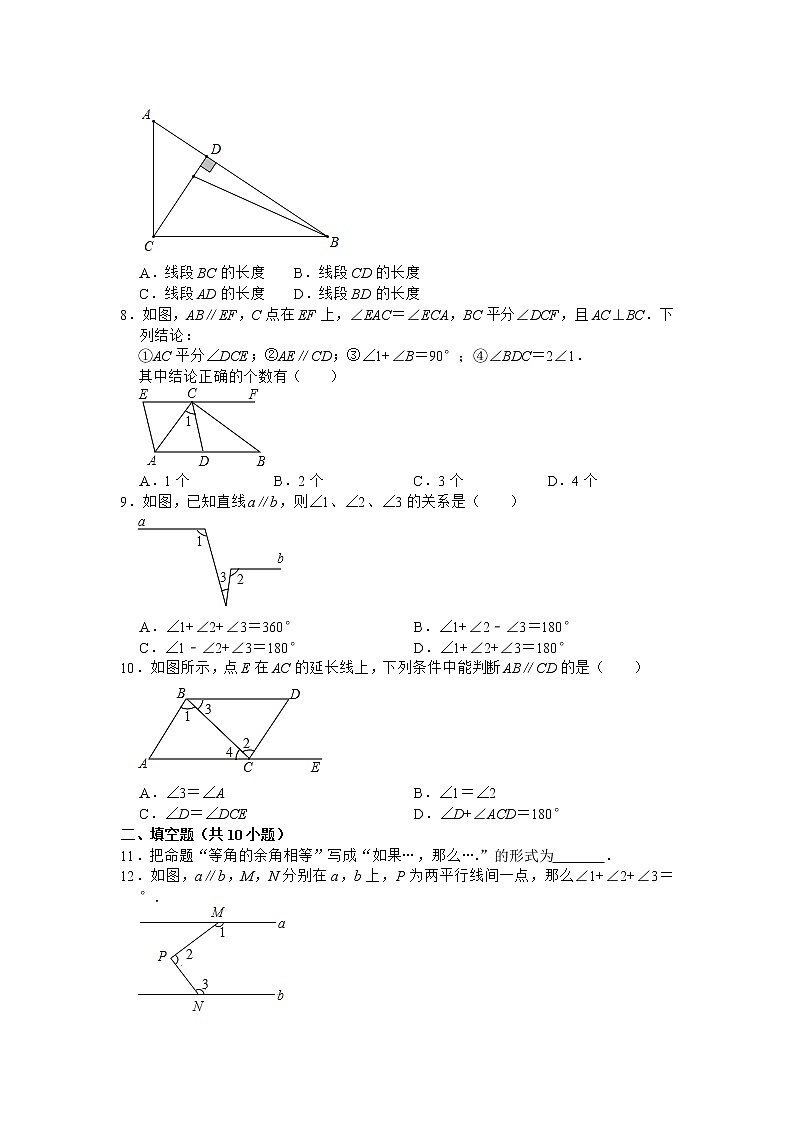
7.如图,∠ACB=90°,CD⊥AB,垂足为D,则点B到直线CD的距离是指( )
A.线段BC的长度 B.线段CD的长度
C.线段AD的长度 D.线段BD的长度
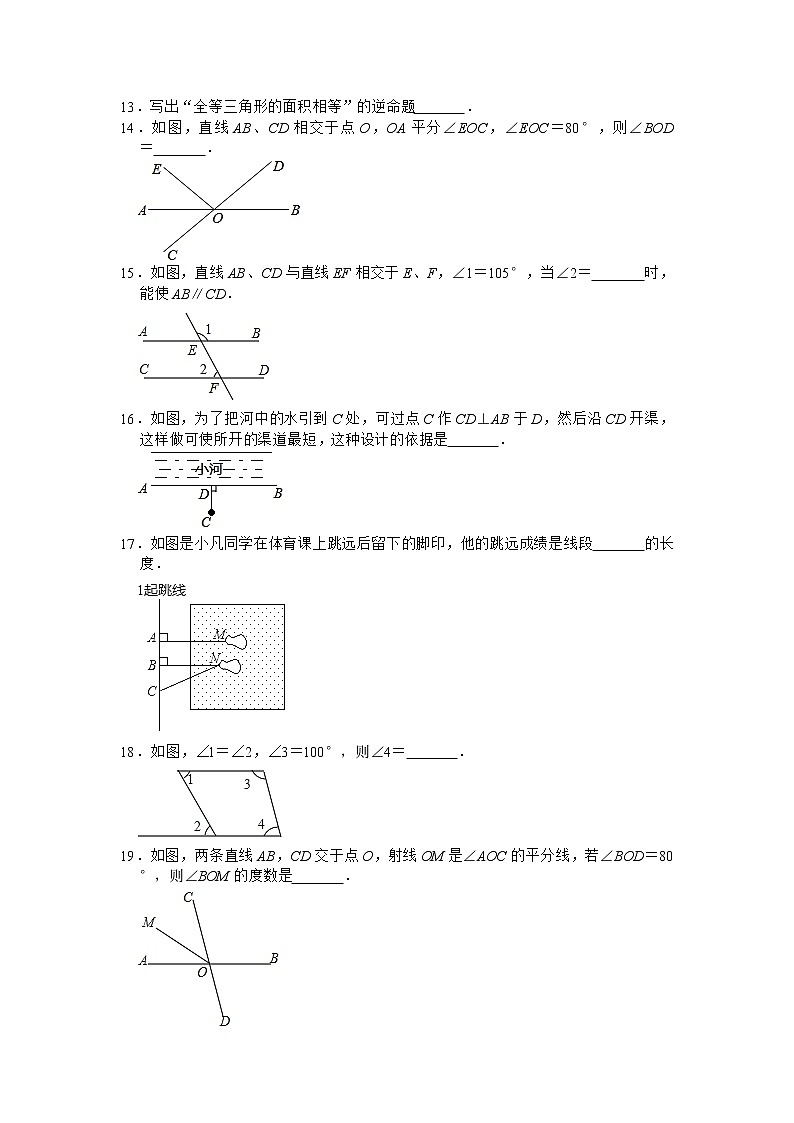
8.如图,AB∥EF,C点在EF上,∠EAC=∠ECA,BC平分∠DCF,且AC⊥BC.下列结论:
①AC平分∠DCE;②AE∥CD;③∠1+∠B=90°;④∠BDC=2∠1.
其中结论正确的个数有( )
A.1个B.2个C.3个D.4个
9.如图,已知直线a∥b,则∠1、∠2、∠3的关系是( )
A.∠1+∠2+∠3=360°B.∠1+∠2﹣∠3=180°
C.∠1﹣∠2+∠3=180°D.∠1+∠2+∠3=180°
10.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠AB.∠1=∠2
C.∠D=∠DCED.∠D+∠ACD=180°
二、填空题(共10小题)
11.把命题“等角的余角相等”写成“如果…,那么….”的形式为 .
12.如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3= °.
13.写出“全等三角形的面积相等”的逆命题 .
14.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD= .
15.如图,直线AB、CD与直线EF相交于E、F,∠1=105°,当∠2= 时,能使AB∥CD.
16.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据是 .
17.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 的长度.
18.如图,∠1=∠2,∠3=100°,则∠4= .
19.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是 .
20.四条直线两两相交,至多会有 个交点.
三、解答题(共10小题)
21.如图,AB∥CD,∠ADC=∠ABC.求证:∠E=∠F.
22.完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE= ( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ( )
∠ABE= ( )
∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠DEB.( )
23.直线a,b,c,d的位置如图所示,已知∠1=58°,∠2=58°,∠3=70°,求∠4的度数.
24.已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.
25.如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=20°,求∠AOC的度数;
(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.
26.在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
(1)请你作出平移后的图形△DEF;
(2)请求出△DEF的面积(每个网格是边长为1的正方形).
27.已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点且∠1+∠2=90°.求证:DE∥BC.
28.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
29.如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
30.如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:A:①②⇒③; B:①③⇒②; C:②③⇒①
请选择一个真命题 进行证明(先写出所选命题,然后证明).
参考答案与试题解析
一、选择题(共10小题)
1.下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短
【分析】根据垂线段最短、直线和线段的性质即可得到结论.
【解答】解:A、从一条河向一个村庄引一条最短的水渠,其中数学原理是:垂线段最短,故原命题错误;
B、两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短,正确;
C、一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线,正确;
D、从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短,正确.
故选:A.
2.如图,OA⊥OB,若∠BOC=34°20',则∠AOC的度数是( )
A.55°20'B.55°40'C.55°60'D.55°80'
【分析】根据互余的意义,利用度、分、秒的计算方法进行计算即可.
【解答】解:∠AOC=∠AOB﹣∠BOC=90°﹣34°20′=55°40′,故选:B.
3.如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
A.5050m2B.5000m2C.4900m2D.4998m2
【分析】根据已知将道路平移,再利用矩形的性质求出长和宽,再进行解答.
【解答】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102﹣2)米,宽为(51﹣1)米.所以草坪的面积应该是长×宽=(102﹣2)(51﹣1)=5000(米2).故选:B.
4.已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是( )
A.相交B.平行C.垂直D.平行或相交
【分析】根据平行公理的推论直接判断直线c与直线a的位置关系即可.
【解答】解:∵在同一平面内,直线a∥b,直线b∥c,∴直线c与直线a的位置关系是:a∥c.故选:B.
5.下列选项中∠1与∠2不是同位角的是( )
A.B.
C.D.
【分析】根据同位角的特征:两条直线被第三条直线所截形成的角中,两个角都在两条被截直线的同侧,并且在第三条直线(截线)的同旁,由此判断即可.
【解答】解:A、∠1和∠2是同位角;B、∠1和∠2是同位角;C、∠1和∠2不是同位角;D、∠1和∠2是同位角;故选:C.
6.如图,将Rt△ABC沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.42B.96C.84D.48
【分析】根据平移的性质得出BE=6,DE=AB=10,则OE=6,则阴影部分面积=S四边形ODFC=S梯形ABEO,根据梯形的面积公式即可求解.
【解答】解:由平移的性质知,BE=6,DE=AB=10,∴OE=DE﹣DO=10﹣4=6,∴S四边形ODFC=S梯形ABEO=(AB+OE)•BE=(10+6)×6=48.故选:D.
7.如图,∠ACB=90°,CD⊥AB,垂足为D,则点B到直线CD的距离是指( )
A.线段BC的长度B.线段CD的长度
C.线段AD的长度D.线段BD的长度
【分析】直线外一点到直线的垂线段的长度,叫做点到直线的距离,根据点到直线的距离的定义解答即可.
【解答】解:∵BD⊥CD于D,∴点B到直线CD的距离是指线段BD的长度.故选:D.
8.如图,AB∥EF,C点在EF上,∠EAC=∠ECA,BC平分∠DCF,且AC⊥BC.下列结论:
①AC平分∠DCE;②AE∥CD;③∠1+∠B=90°;④∠BDC=2∠1.
其中结论正确的个数有( )
A.1个B.2个C.3个D.4个
【分析】由平行线的性质得出∠ECA=∠BAC,∠BCF=∠B,证出∠1+∠BCD=90°,∠ECA+∠BCF=90°,由角平分线定义得出∠BCD=∠BCF,得出∠1=∠ECA,AC平分∠DCE,①正确;证出∠EAC=∠1,得出AE∥CD,②正确;证出∠B=∠BCD,得出∠1+∠B=90°,③正确;由∠1=∠ECA=∠BAC,∠BDC=∠BAC+∠1,得出∠BDC=2∠1,④正确;即可得出结论.
【解答】解:∵AB∥EF,
∴∠ECA=∠BAC,∠BCF=∠B,
∵AC⊥BC,
∴∠BAC=90°,
∴∠1+∠BCD=90°,∠ECA+∠BCF=90°,
∵BC平分∠DCF,
∴∠BCD=∠BCF,
∴∠1=∠ECA,
∴AC平分∠DCE,①正确;
∵∠EAC=∠ECA,
∴∠EAC=∠1,
∴AE∥CD,②正确;
∵∠BCF=∠B,∠BCD=∠BCF,
∴∠B=∠BCD,
∴∠1+∠B=90°,③正确;
∵∠1=∠ECA=∠BAC,∠BDC=∠BAC+∠1,
∴∠BDC=2∠1,④正确;
故选:D.
9.如图,已知直线a∥b,则∠1、∠2、∠3的关系是( )
A.∠1+∠2+∠3=360°B.∠1+∠2﹣∠3=180°
C.∠1﹣∠2+∠3=180°D.∠1+∠2+∠3=180°
【分析】过A作AB∥a,可得a∥AB∥b,依据平行线的性质,即可得到∠1+∠BAD=180°,∠2=∠BAC=∠3+∠BAD,进而得出∠1+∠2﹣∠3=180.
【解答】解:如图,过A作AB∥a,
∵a∥b,
∴AB∥b,
∴∠1+∠BAD=180°,∠2=∠BAC=∠3+∠BAD,
∴∠BAD=∠2﹣∠3,
∴∠1+∠2﹣∠3=180°,
故选:B.
10.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠AB.∠1=∠2
C.∠D=∠DCED.∠D+∠ACD=180°
【分析】根据平行线的判定分别进行分析可得答案.
【解答】解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;故选:B.
二、填空题(共10小题)
11.把命题“等角的余角相等”写成“如果…,那么….”的形式为 如果两个角是相等角的余角,那么这两个角相等 .
【分析】把命题的题设写在如果的后面,把命题的结论部分写在那么的后面即可.
【解答】解:命题“等角的余角相等”写成“如果…,那么….”的形式为:如果两个角是相等角的余角,那么这两个角相等.
故答案为如果两个角是相等角的余角,那么这两个角相等.
【点评】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.
12.如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3= 360 °.
【分析】首先作出PA∥a,根据平行线性质,两直线平行同旁内角互补,可以得出∠1+∠2+∠3的值.
【解答】解:过点P作PA∥a,
∵a∥b,PA∥a,
∴a∥b∥PA,
∴∠1+∠MPA=180°,∠3+∠APN=180°,
∴∠1+∠MPA+∠3+∠APN=180°+180°=360°,
∴∠1+∠2+∠3=360°.
故答案为:360.
13.写出“全等三角形的面积相等”的逆命题 面积相等的三角形全等 .
【分析】首先分清题设是:两个三角形全等,结论是:面积相等,把题设与结论互换即可得到逆命题.
【解答】解:“全等三角形的面积相等”的题设是:两个三角形全等,结论是:面积相等,因而逆命题是:面积相等的三角形全等.
故答案是:面积相等的三角形全等.
14.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD= 40° .
【分析】根据角平分线的定义求出∠AOC,再根据对顶角相等解答.
【解答】解:∵OA平分∠EOC,∠EOC=80°,
∴∠AOC=∠EOC=×80°=40°,
∴∠BOD=∠AOC=40°.
故答案为:40°.
15.如图,直线AB、CD与直线EF相交于E、F,∠1=105°,当∠2= 75° 时,能使AB∥CD.
【分析】因为直线AB、CD与直线EF相交于E、F,所以∠1=∠AEF=105°,则∠AEF与∠2互补时可以使AB∥CD.
【解答】解:∵直线AB、CD与直线EF相交于E、F,
∴∠1=∠AEF=105°;
∵∠AEF与∠2互补时可以使AB∥CD,
∴∠2=180°﹣105°=75°.
∴当∠2=75°时,能使AB∥CD.
故答案为:75°.
【点评】解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养“执果索因”的思维方式与能力.
16.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据是 垂线段最短 .
【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.据此作答.
【解答】解:过D点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,这种设计的依据是垂线段最短.
故答案为:垂线段最短.
17.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 BN 的长度.
【分析】由点到直线的距离的定义及跳远比赛的规则作出分析和判断.
【解答】解:他的跳远成绩是线段BN的长度.
18.如图,∠1=∠2,∠3=100°,则∠4= 80° .
【分析】由∠1=∠2,根据“内错角相等,两直线平行”得到AD∥BC,再根据平行线的性质得到∠3+∠4=180°,即∠4=180°﹣∠3,把∠3=100°代入计算即可.
【解答】解:如图,
∵∠1=∠2,
∴AD∥BC,
∴∠3+∠4=180°,
而∠3=100°,
∴∠4=180°﹣100°=80°.
故答案为80°.
19.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是 140° .
【分析】先根据对顶角相等得出∠AOC=80°,再根据角平分线的定义得出∠COM,最后解答即可.
【解答】解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°,
故答案为:140°.
20.四条直线两两相交,至多会有 6 个交点.
【分析】两条直线相交有一个交点,三条直线两两相交最多有3个交点,四条直线两两相交,至多有6个交点.
【解答】解:如图,可看出四条直线两两相交,至多有6个交点.故填:6.
三、解答题(共10小题)
21.如图,AB∥CD,∠ADC=∠ABC.求证:∠E=∠F.
【分析】直接利用平行线的性质得出∠ABC=∠DCF,再利用已知得出∠E=∠F.
【解答】证明:∵AB∥CD,
∴∠ABC=∠DCF.
又∵∠ADC=∠ABC
∴∠ADC=∠DCF.
∴DE∥BF.
∴∠E=∠F.
22.完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE= ∠ABC ( 两直线平行,同位角相等 )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ∠ADE ( 角平分线定义 )
∠ABE= ∠ABC ( 角平分线定义 )
∴∠ADF=∠ABE
∴ DF ∥ BE ( 同位角相等,两直线平行 )
∴∠FDE=∠DEB.( 两直线平行,内错角相等 )
【分析】根据平行线的性质得出∠ADE=∠ABC,根据角平分线定义得出∠ADF=∠ADE,∠ABE=∠ABC,推出∠ADF=∠ABE,根据平行线的判定得出DF∥BE即可.
【解答】解:理由是:∵DE∥BC(已知),
∴∠ADE=∠ABC(两直线平行,同位角相等),
∵DF、BE分别平分ADE、∠ABC,
∴∠ADF=∠ADE(角平分线定义),
∠ABE=∠ABC(角平分线定义),
∴∠ADF=∠ABE,
∴DF∥BE(同位角相等,两直线平行),
∴∠FDE=∠DEB(两直线平行,内错角相等),
故答案为:∠ABC,两直线平行,同位角相等;∠ADE,角平分线定义;∠ABC,角平分线定义;DF,BE,同位角相等,两直线平行;两直线平行,内错角相等.
23.直线a,b,c,d的位置如图所示,已知∠1=58°,∠2=58°,∠3=70°,求∠4的度数.
【分析】由已知得出∠1=∠2=58°,证出a∥b,得出∠5=∠3=70°,再由平角的定义即可得出∠4的度数.
【解答】解:如图所示,
∵∠1=58°,∠2=58°,
∴∠1=∠2=58°,
∴a∥b,
∴∠5=∠3=70°,
∴∠4=180°﹣∠5=110°.
24.已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.
【分析】由∠A=∠F,根据内错角相等,两直线平行,即可求得AC∥DF,即可得∠C=∠FEC,又由∠C=∠D,则可根据同位角相等,两直线平行,证得BD∥CE.
【解答】证明:∵∠A=∠F,
∴AC∥DF,
∴∠C=∠FEC,
∵∠C=∠D,
∴∠D=∠FEC,
∴BD∥CE.
25.如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=20°,求∠AOC的度数;
(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.
【分析】(1)利用垂直的定义,∠AOE=90°,即可得出结果;
(2)利用邻补角的定义,解得∠AOC=60°,有对顶角的定义,得∠BOD=60°,解得∠EOD.
【解答】解:(1)∵OE⊥AB,
∴∠AOE=90°,
∵∠EOD=20°,
∴∠AOC=180°﹣90°﹣20°=70°;
(2)设∠AOC=x,则∠BOC=2x,
∵∠AOC+∠BOC=180°,
∴x+2x=180°,
解得:x=60°,
∴∠AOC=60°,
∴∠BOD=60°,
∴∠EOD=180°﹣90°﹣60°=30°.
26.在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
(1)请你作出平移后的图形△DEF;
(2)请求出△DEF的面积(每个网格是边长为1的正方形).
【分析】(1)根据网格结构找出点B、C的对应点E、F的位置,然后与点D顺次连接即可;
(2)利用△DEF所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【解答】解:(1)△DEF如图所示;
(2)由图可知,S△DEF=3×4﹣×2×4﹣×2×3﹣×2×1,=12﹣4﹣3﹣1,=4.
27.已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点且∠1+∠2=90°.求证:DE∥BC.
【分析】依据同角的余角相等,即可得到∠3=∠2,即可得出DE∥BC.
【解答】证明:∵CD⊥AB(已知),
∴∠1+∠3=90°(垂直定义).
∵∠1+∠2=90°(已知),
∴∠3=∠2(同角的余角相等).
∴DE∥BC(内错角相等,两直线平行).
【点评】本题主要考查了平行线的判定,解题时注意:内错角相等,两直线平行.
28.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
【分析】由AB∥CF,∠ABC=70°,易求∠BCF,又DE∥CF,∠CDE=130°,那么易求∠DCF,于是∠BCD=∠BCF﹣∠DCF可求.
【解答】解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°,
∴∠DCF=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.
29.如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
【分析】(1)根据角平分线的定义求出∠AOC=45°,然后根据邻补角的定义求解即可;
(2)设∠NOB=x°,∠BOC=4x°,根据角平分线的定义表示出∠COM=∠MON=∠CON,再根据∠BOM列出方程求解x,然后求解即可.
【解答】解(1)∵∠AOM=90°,OC平分∠AOM,
∴∠AOC=∠AOM=×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°﹣∠AOC=180°﹣45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB﹣∠BON=4x°﹣x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=∠CON=x°,
∵∠BOM=x+x=90°,
∴x=36°,
∴∠MON=x°=×36°=54°,
即∠MON的度数为54°.
30.如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:A:①②⇒③; B:①③⇒②; C:②③⇒①
请选择一个真命题 ①③② 进行证明(先写出所选命题,然后证明).
【分析】根据全等三角形的判定定理和性质定理证明即可.
【解答】已知:AB=AC,BD=CE,
求证:AD=AE.
证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴AD=AE.
故答案为:①③②.
初中数学北京课改版七年级上册3.10 相交线与平行线单元测试随堂练习题: 这是一份初中数学北京课改版七年级上册3.10 相交线与平行线单元测试随堂练习题,共19页。
2020-2021学年人教新版七年级下册数学期末练习试题(word解析版): 这是一份2020-2021学年人教新版七年级下册数学期末练习试题(word解析版),共15页。试卷主要包含了9的平方根是,三角形的外角和等于,下列命题是真命题的个数为,下列说法正确的是,将点A等内容,欢迎下载使用。
2020-2021学年人教新版七年级下册数学期末冲刺试题(有答案): 这是一份2020-2021学年人教新版七年级下册数学期末冲刺试题(有答案),共17页。试卷主要包含了下列实数,下列各式计算正确的是,下列调查中,适合用普查方式的是,下列说法正确的是,如图,给出下列条件,在平面直角坐标系中,点P等内容,欢迎下载使用。













