考点01 二次函数的图象与性质-2021年中考数学一轮复习基础夯实（安徽专用）

这是一份考点01 二次函数的图象与性质-2021年中考数学一轮复习基础夯实（安徽专用），文件包含考点01二次函数的图象与性质原卷版docx、考点01二次函数的图象与性质解析版docx等2份试卷配套教学资源，其中试卷共43页， 欢迎下载使用。

考点一 二次函数的图像与性质
知识点整合
一、二次函数的概念
一般地，形如y=ax2+bx+c（a，b，c是常数，a≠0）的函数，叫做二次函数．
二、二次函数解析式的三种形式
（1）一般式：y=ax2+bx+c（a，b，c为常数，a≠0）．
（2）顶点式：y=a（x–h）2+k（a，h，k为常数，a≠0），顶点坐标是（h，k）．
（3）交点式：y=a（x–x1）（x–x2），其中x1，x2是二次函数与x轴的交点的横坐标，a≠0．
三、二次函数的图象及性质
1．二次函数的图象与性质
解析式
二次函数y=ax2+bx+c（a，b，c是常数，a≠0）
对称轴
x=–
顶点
（–，）
a的符号
a>0
a<0
图象


开口方向
开口向上
开口向下
最值
当x=–时，
y最小值=
当x=–时，
y最大值=
最点
抛物线有最低点
抛物线有最高点
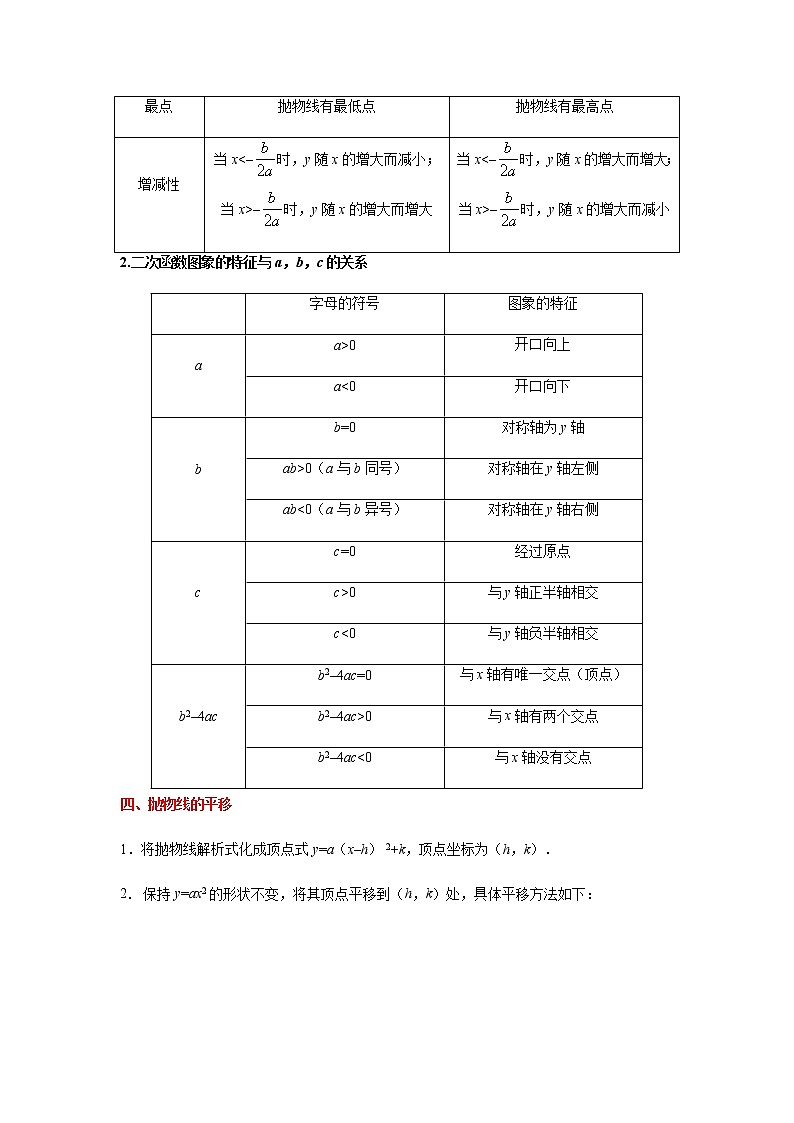
增减性
当x<–时，y随x的增大而减小；当x>–时，y随x的增大而增大
当x<–时，y随x的增大而增大；当x>–时，y随x的增大而减小
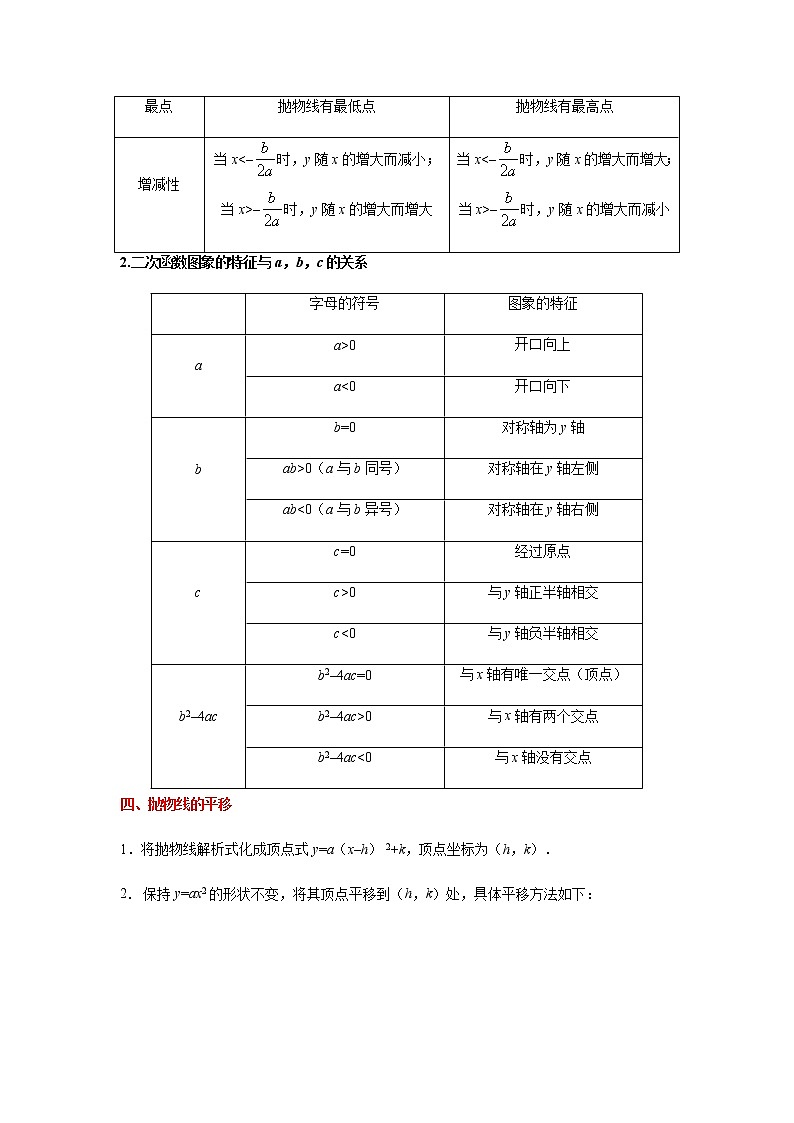
2.二次函数图象的特征与a，b，c的关系

字母的符号
图象的特征
a
a>0
开口向上
a<0
开口向下
b
b=0
对称轴为y轴
ab>0（a与b同号）
对称轴在y轴左侧
ab<0（a与b异号）
对称轴在y轴右侧
c
c=0
经过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
b2–4ac
b2–4ac=0
与x轴有唯一交点（顶点）
b2–4ac>0
与x轴有两个交点
b2–4ac<0
与x轴没有交点
四、抛物线的平移
1．将抛物线解析式化成顶点式y=a（x–h） 2+k，顶点坐标为（h，k）．
2．保持y=ax2的形状不变，将其顶点平移到（h，k）处，具体平移方法如下：

3．注意
二次函数平移遵循“上加下减，左加右减”的原则，据此，可以直接由解析式中常数的加或减求出变化后的解析式；二次函数图象的平移可看作顶点间的平移，可根据顶点之间的平移求出变化后的解析式．
考向一 二次函数的有关概念
1．二次函数的一般形式的结构特征：①函数的关系式是整式；②自变量的最高次数是2；③二次项系数不等于零．
2．一般式，顶点式，交点式是二次函数常见的表达式，它们之间可以互相转化．
典例引领
1．（2020·湖北巴东县·九年级期中）已知二次函数，则的值为（ ）
A． B． C．3 D．
【答案】A
【分析】
根据二次函数的定义列出关于m的不等式组，求出m的值即可．
【详解】
解：∵函数是二次函数，
，解得，
故选：A
【点睛】
本题考查的是二次函数的定义，即一般地，形如y=ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．
2．（2019·张掖育才中学九年级月考）下列函数是二次函数的有（　　）
（1）y＝1﹣x2；（2）y＝；（3）y＝x（x﹣3）；（4）y＝ax2+bx+c；（5）y＝2x+1；（6）y＝2（x+3）2﹣2x2．
A．1个 B．2个 C．3个 D．4个
【答案】B
【分析】
根据二次函数的定义逐个判断即可得．
【详解】
（1）函数是二次函数；
（2）函数不是二次函数；
（3）函数整理为，是二次函数；
（4）只有当时，函数才是二次函数；
（5）函数是一次函数；
（6）函数整理为，是一次函数；
综上，是二次函数的为（1）（3），共有2个，
故选：B．
【点睛】
本题考查了二次函数，熟练掌握二次函数的定义是解题关键．
变式拓展
1．（2020·四川省绵阳外国语学校九年级期中）已知y=+2m是关于x的二次函数，则下列说法正确的是（　　）
A．有最大值4 B．有最大值-4
C．有最小值4 D．有最小值-4
【答案】B
【分析】
根据二次函数的定义列出方程求解m，然后根据二次函数的性质计算即可．
【详解】
由二次函数的定义可得，
∴m=-2．
此时二次函数解析式为y=-4x2-4，
图象开口向下，有最大值-4．
故选：B．
【点睛】
本题考查了二次函数的定义和性质，掌握知识点是解题关键．
2．（2020·安徽休宁县·九年级月考）如图，等腰的直角边与正方形DEFG的边长均为2，且AC与DE在同一直线上，开始时点C与点D重合，让沿这条直线向右平移，直到点A与点E重合为止设CD的长为x，与正方形DEFG重合部分图中阴影部分的面积为y，则y与x之间的函数关系的图象大致是（ ）

A． B．
C． D．
【答案】A
【分析】
由题意写出y与x之间的函数关系式可以得到其图象．
【详解】
解：由题意可以得到y与x之间的函数关系式为：
，

所以y与x之间的函数关系的图象大致是：


故选A ．
【点睛】
本题考查函数及其图象，由题意列出函数关系式是解题关键．
3．（2020·达拉特旗第八中学九年级月考）如果函数是二次函数，则的取值范围是（ ）
A． B． C．＝﹣2 D．为全体实数
【答案】C
【分析】
根据二次函数定义可得m-2≠0，，再解即可．
【详解】
解：由题意得：m-2≠0，，
解得：m=-2，
故选：C．
【点睛】
此题主要考查了二次函数定义，关键是掌握形如y=ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．
考向二 二次函数的图象
二次函数的图象是一条关于某条直线对称的曲线，叫做抛物线，该直线叫做抛物线的对称轴，对称轴与抛物线的交点叫做抛物线的顶点.
典例引领
1．（2020·黑龙江塔河县·九年级期末）抛物线y＝2x2， y＝－2x2， y＝x2的共同性质是（ ）
A．开口向上 B．对称轴是y轴 C．都有最高点 D．y随x的增大而增大
【答案】B
【分析】
根据二次函数的图象与性质解题．
【详解】
抛物线y＝2x2， y＝x2 开口向上，对称轴是对称轴是y轴，有最低点，在y轴的右侧，y随x的增大而增大，y＝－2x2，开口向下，对称轴是对称轴是y轴，有最高点，在y轴的左侧，y随x的增大而增大，
故抛物线y＝2x2， y＝－2x2， y＝x2的共同性质是对称轴是y轴，
故选：B．
【点睛】
本题考查二次函数图象的性质，是重要考点，难度较易，掌握相关知识是解题关键．
2．（2020·浙江省杭州市萧山区高桥初级中学九年级期中）已知二次函数，则当时，该函数( )
A．有最大值7，有最小值4 B．只有最大值7，无最小值
C．只有最小值3，无最大值 D．有最小值3，有最大值7
【答案】D
【分析】
由可得：抛物线的开口向上，抛物线的对称轴为 所以当时，随的增大而减小，当时，随的增大而增大，再根据函数的增减性求解函数的最大值与最小值，再逐一判断各选项可得答案．
【详解】
解：
抛物线的开口向上，抛物线的对称轴为

所以当时，随的增大而减小，
当时，函数值有最大值：当时，函数值有最小值：
当时，随的增大而增大，
当时，函数值有最小值： 当时，函数值有最大值：
综上：函数值最大为 最小为
所以：错误，正确；
故选：
【点睛】
本题考查的是二次函数的增减性，二次函数的最值问题，掌握二次函数的增减性是解题的关键．
3．（2020·浙江省温岭市第四中学九年级期中）已知函数经过A（m，）、B（m−1，），若．则m的取值范围是（ ）
A． B． C． D．
【答案】B
【分析】
由图像开口向下，对称轴为y=0知，要使，需使A点更靠近对称轴y轴，由此列出关于m的不等式解之即可 ．
【详解】
解：∵图像开口向下，对称轴为y=0且
∴，下面解此不等式．
第一种情况，当m＜0时，得，解得m＜0；
第二种情况，当时，得，解得；
第三种情况，当时，得，解得，无解；
综上所述得．
故选：B．
【点睛】
此题考查二次函数的图像与性质，比较图像上两点的函数值．其关键是，当二次函数开口向下时，图像上的点越靠近对称轴时，函数值越大；当二次函数开口向上时，图像上的点越靠近对称轴时，函数值越小．
4．（2020·东阳市南马镇初级中学九年级月考）设二次函数，点在该函数对称轴上，则点的坐标可能是（ ）
A．（1，0） B．（，0） C．（3，0） D．（0，）
【答案】C
【分析】
由抛物线解析式可求得其对称轴，则可求得M点的横坐标，可求得答案．
【详解】
∵，
∴抛物线对称轴为，
∵点M在抛物线对称轴上，
∴点M的横坐标为3，
故选：C．
【点睛】
本题主要考查了二次函数的性质，掌握二次函数的顶点式是解题的关键，即在中，顶点坐标为（h，k），对称轴为．
变式拓展
1．（2020·鹿泉市李村镇联合中学九年级月考）如图，在直角坐标系的第一象限内，是边长为2的等边三角形，设直线截这个三角形所得位于直线左侧的图形（阴影部分）的面积为S，则S关于t的大致函数图象是（　　　）

A． B．
C． D．
【答案】C
【分析】
分0≤t≤1和1＜t≤2两种情况，利用三角形的面积公式，可以表示出S与t的函数关系式，即可做出选择．
【详解】
解：①当0≤t≤1时，如图，

∵l∥y轴，△AOB为等边三角形，
∴∠COD=60°，
∴OD=t，CD=OD·tan60°=t，
∴，
即S=(0≤t≤1)，
故S与t之间的函数关系式的图像应为自变量在0≤t≤1、开口向上的二次函数图像；
②当1＜t≤2时，如图，∠CBD=60°，BD=2﹣t，

∴CD=BD·tan60°=（2﹣t），
∴，
即(1＜t≤2)，
∴故S与t之间的函数关系式的图像应为自变量在1＜t≤2、开口向下的二次函数图像，
故选：C．
【点睛】
本题考查三角形的面积公式、二次函数图像特征、解直角三角形、60°角的正切值，正确列出函数关系式，掌握二次函数图像是解答的关键，注意实际问题的图像只是一部分．
2．（2020·陆丰市甲东中学九年级月考）已知二次函数，当时，随着的增大而增大，当时，随的增大而减小，当时，的值为（ ）
A．2 B． C．4 D．
【答案】D
【分析】
根据题意可得二次函数的对称轴x=-2，进而可得h的值，从而可得函数解析式，再把x=0代入函数解析式可得y的值．
【详解】
由题意得：二次函数y=-（x+h）2的对称轴为x=-2，
∴h=2
∴函数解析式，
∴当时，
故选D.
【点睛】
此题主要考查了二次函数的性质，关键是掌握二次函数顶点式y=a（x-h）2+k，对称轴为x=h.
3．（2020·宁波市曙光中学九年级月考）已知点，，都在函数的图象上，则，，的大小关系是（ ）．
A． B． C． D．
【答案】A
【分析】
先根据抛物线解析式确定二次函数的抛物线的开口方向和对称轴，然后再根据点与对称轴越近、对应的函数值越小解答即可．
【详解】
解：∵抛物线，
∴抛物线开口向上，对称轴为,
∵点，，
∵与对称轴的距离分别为，，，
∵，
∴．
故答案为A．
【点睛】
本题主要考查了利用二次函数求最值，掌握当函数的开口方向向上，当点与对称轴越近、对应的函数值越小成为解答本题的关键．
4．（2020·浙江瑞安市·九年级期中）抛物线的图象如图所示．已知点，，三点都在该图象上，则，，的大小关系为（　　　）

A． B． C． D．
【答案】C
【分析】
根据函数解析式的特点为顶点式，其对称轴为x=-3，图象开口向下；根据二次函数图象的对称性，利用在对称轴的左侧，y随x的增大而增大，可判断y2>y1>y3．
【详解】
由二次函数y=a(x+3)2+k可知对称轴为x=−3，根据二次函数图象的对称性可知， 与对称，
∵点，， )在对称轴的左侧，y随x的增大而增大，
∵-4>-5>-6.5，
∴y2>y1>y3，
故选C.
【点睛】
本题考查了函数图象上的点的坐标与函数解析式的关系，同时考查了函数的对称性及增减性.
考向三 二次函数的性质
二次函数的解析式中，a决定抛物线的形状和开口方向，h、k仅决定抛物线的位置．若两个二次函数的图象形状完全相同且开口方向相同，则它们的二次项系数a必相等．
典例引领
1．（2020·德庆县九市中学九年级月考）把二次函数y=a(x-h)2+k的图象先向左平移2个单位，再向上平移4个单位，得到二次函数y=(x+1)2-1的图象.
（1）试确定a，h，k的值；
（2）指出二次函数y=a(x-h)2+k的开口方向，对称轴和顶点坐标.
【答案】（1） （2）开口向下，对称轴是x=1的直线，顶点（1，-5）
【解析】
试题分析：（1）二次函数的平移，可以看作是将二次函数y= (x+1)2-1先向右平移2个单位，再向下平移4个单位得到二次函数y=a(x-h)2+k，然后再按二次函数图象的平移法则，确定函数解析式，即可得到结论；
（2），直接根据函数解析式，结合二次函数的性质，进行回答即可.
试题分析：（1）∵二次函数y=a(x-h)2+k的图象先向左平移2个单位，再向上平移4个单位，得到二次函数y= (x+1)2-1，
∴可以看作是将二次函数y= (x+1)2-1先向右平移2个单位，再向下平移4个单位得到二次函数y=a(x-h)2+k，
而将二次函数y= (x+1)2-1先向右平移2个单位，再向下平移4个单位得到二次函数为：y= (x-1)2-5，
∴a=，b=1，k=-5；
（2）二次函数y= (x-1)2-5，
开口向上，对称轴为x=1，顶点坐标为（1，-5）.
2．（2020·全国九年级课时练习）已知 是二次函数，且函数图象有最高点．
（1）求k的值；
（2）求顶点坐标和对称轴，并说明当x为何值时，y随x的增大而减少．
【答案】（1）k=﹣3；（2）当k=﹣3时，y=﹣x2顶点坐标（0，0），对称轴为y轴，当x＞0时，y随x的增大而减少．
【解析】
试题分析：（1）根据二次函数的定义得出k2+k﹣4=2，再利用函数图象有最高点，得出k+2＜0，即可得出k的值；
（2）利用（1）中k的值得出二次函数的解析式，利用形如y=ax2（a≠0）的二次函数顶点坐标为（0，0），对称轴是y轴即可得出答案．
试题解析：解：（1）∵是二次函数，∴k2+k﹣4=2且k+2≠0，解得k=﹣3或k=2．∵函数有最高点，∴抛物线的开口向下，∴k+2＜0，解得k＜﹣2，∴k=﹣3；
（2）当k=﹣3时，二次函数为y=﹣x2，顶点坐标为（0，0），对称轴为y轴，当x＞0时，y随x的增大而减少．
3．（2020·安徽九年级专题练习）已知抛物线与轴有两个不同的交点.
(1)求的取值范围；
(2)若抛物线经过点和点，试比较与的大小，并说明理由.
【答案】(1) 的取值范围是； (2). 理由见解析.
【解析】
【分析】
（1）由二次函数与x轴交点情况，可知△＞0；
（2）求出抛物线对称轴为直线x=1，由于A（2，m）和点B（3，n）都在对称轴的右侧，即可求解；
【详解】
(1).
由题意，得，
∴
∴的取值范围是.
(2). 理由如下:
∵抛物线的对称轴为直线，
又∵，
∴当时，随的增大而增大.
∵，∴.
【点睛】
本题考查二次函数图象及性质；熟练掌握二次函数对称轴，函数图象的增减性是解题的关键．
4．（2018·全国九年级专题练习）在直角坐标系中，二次函数图象的顶点为A（1、﹣4），且经过点B（3，0）．
（1）求该二次函数的解析式；
（2）当﹣3＜x＜3时，函数值y的增减情况；
（3）将抛物线怎样平移才能使它的顶点为原点．
【答案】（1）y=（x﹣1）2﹣4;（2）当﹣3＜x＜1时，y随x的增大而减小，当1≤x＜3，y随x的增大而增大;（3）将抛物线y=（x﹣1）2﹣4向左平移1个单位，再向上平移4个单位即可实现抛物线顶点为原点．
【分析】
（1）由已知条件可设二次函数的解析式为：，再代入点（3，0）解出a的值即可得到二次函数的解析式；
（2）由（1）中所求解析式可得第（2）问答案；
（3）根据（1）中所得解析式可确定原来顶点的位置，这样就可确定怎样平移可将顶点移到原点了.
【详解】
（1）∵二次函数图象的顶点为A（1，﹣4），
∴可设二次函数的解析式为y=a（x﹣1）2﹣4，
又∵二次函数图象过点B（3，0）
∴a（3﹣1）2﹣4=0，解得：a=1，
∴y=（x﹣1）2﹣4
（2）∵抛物线对称轴为直线x=1，且开口向上，
∴当﹣3＜x＜1时，y随x的增大而减小；当1≤x＜3，y随x的增大而增大，
（3）将抛物线y=（x﹣1）2﹣4向左平移1个单位，再向上平移4个单位即可实现抛物线顶点为原点．
【点睛】
（1）当已知抛物线的顶点坐标，求解析式时，一般把解析式设为顶点式：的形式；（2）本题中顶点的横坐标x=1在﹣3＜x＜3内，因此要分为：①﹣3＜x＜1和②1≤x＜3两段来讨论函数值y的增减情况；（3）将抛物线进行平移时，“h”的值是“左移加，右移减”；“k”的值是“上移加，下移减”.
变式拓展
1．（2020·河北九年级专题练习）在平面直角坐标系中，已知抛物线和直线l:y=kx+b，点A(-3,-3)，B(1,-1)均在直线l上．
（1）若抛物线C与直线l有交点，求a的取值范围；
（2）当a=-1，二次函数的自变量x满足m≤x≤m+2时，函数y的最大值为-4，求m的值；
（3）若抛物线C与线段AB有两个不同的交点，请直接写出a的取值范围．
【答案】（1）a≤且a≠0；（2）m=-3或m=3；（3）或a≤-2；
【分析】
（1）点，代入，求出；联立与，则有，即可求解；
（2）根据题意可得，，当时，有，或；①在左侧，随的增大而增大，时，有最大值，；
②在对称轴右侧，随最大而减小，时，有最大值；
（3）①时，时，，即；
②时，时，，即，直线的解析式为，抛物线与直线联立：，，则，即可求的范围.
【详解】
解：（1）点，代入，
，
，
；
联立与，则有，
抛物线与直线有交点，
，
a≤且a≠0；
（2）根据题意可得，，
，
抛物线开口向下，对称轴，
时，有最大值，
∴当时，有，
或，
①在左侧，随的增大而增大，
时，有最大值，
；
②在对称轴右侧，随最大而减小，
时，有最大值；
综上所述：m=-3或m=3；
（3）①时，时，，
即；
②时，时，，
即，
直线的解析式为，
抛物线与直线联立：，
，
，
，
的取值范围为或a≤-2.
【点睛】
本题考查二次函数的图象及性质，一次函数的图象及性质；熟练掌握待定系数法求解析式，数形结合，分类讨论函数在给定范围内的最大值是解题的关键．
2．（2018·黑龙江牡丹江市·中考真题）如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，交y轴于点C，点D为抛物线的顶点，连接BD，点H为BD的中点．请解答下列问题：
（1）求抛物线的解析式及顶点D的坐标；
（2）在y轴上找一点P，使PD+PH的值最小，则PD+PH的最小值为　 　．
（注：抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=﹣，顶点坐标为（﹣，）

【答案】（1）y=﹣x2+2x+3，D（1，4）（2）
【分析】
(1)直接将A、B两点坐标代入抛物线解析式，用待定系数法可求得抛物线解析式；
(2)求得点H关于y轴的对称点H′，连接H′D与y轴交于点P，此时PD+PH最小.
【详解】
（1）∵抛物线y=﹣x2+bx+c过点A（﹣1，0），B（3，0）
∴
解得
∴所求函数的解析式为：y=﹣x2+2x+3
y=﹣x2+2x+3=﹣（x﹣1）2+4
∴顶点D（1，4）
（2）∵B（3，0），D（1，4）
∴中点H的坐标为（2，2）其关于y轴的对称点H′坐标为（﹣2，2）
连接H′D与y轴交于点P，则PD+PH最小
且最小值为： =
∴答案：
【点睛】
本题主要考查二次函数的图像与性质，解题的关键是用待定系数法求出函数解析式后灵活找出点H关于y轴的对称点H′求解.
3．（2019·全国九年级课时练习）已知函数.
（1）写出函数图象的开口方向、对称轴、顶点坐标；
（2）求出图象与x轴的交点坐标，与y轴的交点坐标；
（3）当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减小？
（4）当x取何值时，函数有最大值（或最小值）？并求出最大（或小）值？
【答案】（1）抛物线的开口向上，对称轴是直线，顶点坐标是（-1,-8）；（2）图象与y轴交于（0,-6）；（3）得当时，y随x的增大而增大；当时，y随x的增大而减小；（4）由顶点坐标，得当时，y有最小值，最小值是-8.
【解析】
【分析】
（1）根据二次函数性质，即可得到答案；
（2）令y=0，x=0，分别代入解析式，即可得到与坐标轴交点坐标；
（3）根据二次函数的性质，即可得解；
（4）根据二次函数的性质，以及a的值，即可得到答案.
【详解】
解：（1）由函数，
∵，，，
∴抛物线的开口向上，对称轴是直线，顶点坐标是（-1,-8）.
（2）令，即，
解得，.
∴图象与x轴交于（1,0），（-3,0）.
令，即，
∴图象与y轴交于（0,-6）.
（3）由二次函数的性质，得：当时，y随x的增大而增大；当时，y随x的增大而减小.
（4）由顶点坐标，得：当时，y有最小值，最小值是-8.
【点睛】
本题考查了二次函数的性质，解题的关键是熟练掌握性质，并正确求出与坐标轴的交点坐标.
4．（2020·全国）在平面直角坐标系中，若抛物线与直线交于点和点，其中，点为原点，求的面积.

【答案】.
【分析】
首先求得两个交点的坐标，然后求得直线与y轴的交点坐标，再根据三角形的面积公式即可得出答案．
【详解】
解：由题意得：

解得：或
∵点和点，其中
∴，
直线与y轴的交点坐标为：（0，1）
∴
【点睛】
考查了二次函数的性质，解题的关键是了解如何求得两个图象的交点坐标．
5．（2019·河南九年级专题练习）如图， 已知抛物线的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点 ．
（1）求抛物线的解析式和A、B两点的坐标；
（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；
（3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标 ．

【答案】（1），点A的坐标为(-2，0)，点B的坐标为(8，0)；（2）存在点P，使△PBC的面积最大，最大面积是16，理由见解析；（3）点M的坐标为(4-2，)、(2，6)、(6，4)或(4+2，-)．
【分析】
（1） 由抛物线的对称轴为直线x=3，利用二次函数的性质即可求出a值， 进而可得出抛物线的解析式， 再利用二次函数图象上点的坐标特征， 即可求出点A、B的坐标；
（2） 利用二次函数图象上点的坐标特征可求出点C的坐标， 由点B、C的坐标， 利用待定系数法即可求出直线BC的解析式， 假设存在， 设点P的坐标为（x,），过点P作PD//y轴， 交直线BC于点D，则点D的坐标为（x,），PD=- x2+2x，利用三角形的面积公式即可得出三角形PBC的面积关于x的函数关系式， 再利用二次函数的性质即可解决最值问题；
（3） 设点M的坐标为（m,），则点N的坐标为（m,），进而可得出MN，结合MN=3即可得出关于m的含绝对值符号的一元二次方程， 解之即可得出结论 ．
【详解】
（1）抛物线的对称轴是直线，
，解得：，
抛物线的解析式为．
当时，，
解得：，，
点的坐标为，点的坐标为．
（2） 当时，，
点的坐标为．
设直线的解析式为．
将、代入，
，解得：，
直线的解析式为．
假设存在， 设点的坐标为，过点作轴， 交直线于点，则点的坐标为，如图所示 ．
，
．
，
当时，的面积最大， 最大面积是 16 ．
，
存在点，使的面积最大， 最大面积是 16 ．
（3） 设点的坐标为，则点的坐标为，
．
又，
．
当时， 有，
解得：，，
点的坐标为或；
当或时， 有，
解得：，，
点的坐标为，或，．
综上所述：点的坐标为，、、或，．

【点睛】
本题考查了二次函数的性质、 二次函数图象上点的坐标特征、 待定系数法求一次函数解析式以及三角形的面积， 解题的关键是： （1） 利用二次函数的性质求出a的值； （2） 根据三角形的面积公式找出关于x的函数关系式； （3） 根据MN的长度， 找出关于m的含绝对值符号的一元二次方程 ．